兩種歐拉函數模闆

求歐拉函數代碼的方式：​

​直接求​

​​和​

​打表​

​ 歐拉函數的作用：一個數n，求小于n的互質的個數。特例：1——oula（1）=1；

歐拉函數的公式：

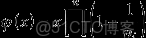
其中i為x所有質因數。注意：每種質因數隻一個

為什麼會這樣？首先，互質的兩個數一定不能有公共因數。比如9和7互質，9和12不互質，因為有共同因數3.

那麼我難道需要一個個循環比較嗎？

答案先然不可能，因為如果數值過大這是個很大的複雜度。那麼我該如何處理？

換一種思維。比如求24中的互質個數。答案是1，5，7，11，13，17，19，23。共8個

1. 24=2 * 2 * 2 * 3；那麼在小于12中的數的核心共同質數為2的倍數或者三的倍數。有人可能說明明還要4，6的倍數，那是因為這些倍數囊括在2，3之中。是以我們每個質因數隻記錄一個。
2. 看在24中，有1/2的是2的倍數，也就是1/2的數是和24有共同因數2.那麼就有（1-1/2）的數和24沒有共同因數2；
3. 同理那麼就有1/3的數和24有共同因數3，并且（1-1/3）=2/3的數沒有共同因數3.那麼沒有因數2和因數三剩下的不就是和24互質麼，那麼機率=（1-1/2）* （1-1/3）=1/3.總個數為24*1/3=8滿足要求。
4. 如果一個因數出現多次怎麼排除呢。或者怎麼防止4，6這些數被計入因數中，這就要用到質因數分解的思想。隻不過我們不需要這個幂出現的次數，隻需要讓剩餘的不可能在存在目前這個數為因數的可能性。

附上直接求代碼：

private static int oula(int team) {
    int i=0;int res=team;int team1=team;
    for(i=2;i<(int)Math.sqrt(team1) 1;i )
    {
      if(team%i==0) {
        res=res/i*(i-1);
        while(team%i==0) {team/=i;}//保證沒有i作為因子     
      }
    }
    if(team>1)res=res/team*(team-1);//說明後面還有一個比較大的互質因數大小為team
    return res;
  }      

其中，res為結果，team1作為求因數用。如果實在不能了解，好好看下質因數分解。

int a[]=new int[1000001];
 for(int i=1;i<1000001;i )
 {
   a[i]=i;
 }
 for(int i=2;i 2<1000001;i =2)
 {
   a[i]/=2;
 }
 for(int i=3;i 2<1000001;i =2)
 {
   if(a[i]==i)
   {
     for(int j=i;j i<=1000001;j =i)
     {
       a[j]=a[j]/i*(i-1);
     }
   }
 }