紅黑樹具體實作與代碼分析

一：背景

紅黑樹（英語：Red–Black Tree，簡稱 RB-Tree）是一種平衡的二叉查找樹，用途廣泛。例如：

Java 中的：java.util.TreeMap，java.util.TreeSet；

C++ STL 中的：map，multimap，multiset。

它是在 1972 年由 Rudolf Bayer 發明的，他稱之為 “對稱二叉 B 樹”，它現代的名字（即 “紅黑樹”）是 Leo J. Guibas 和 Robert Sedgewick 于 1978 年寫的一篇論文中獲得的。

紅黑樹的實作比較複雜，但它的操作有着良好的最壞情況運作時間，并且在實踐中是高效的，它可以在 O(logn) 時間内做查找，插入和删除操作。

紅黑樹有四個性質（也有書籍和部落格上說是五個性質，其實四個性質足矣）：

每個結點要麼是紅的，要麼是黑的；

根結點是黑色的；

如果一個結點是紅色的，則它的兩個孩子都是黑色的；

對于任意一個結點，其到葉子結點的每條路徑上都包含相同數目的黑色結點。

二：具體實作與代碼分析

和 AVL 樹通過限制左右子樹高度不同，紅黑樹是通過它的四條性質來實作 “平衡狀态”，在插入結點或者删除結點時，可能會造成某個結點違反了上述的某條性質，那麼紅黑樹的做法就是通過 “重新着色” 和 “旋轉” 兩種方式使之重新符合性質。

“重新着色” 這很簡單，現在來看下 “旋轉” 是怎麼旋轉的。一共有兩種旋轉方式：左旋和右旋。

左旋

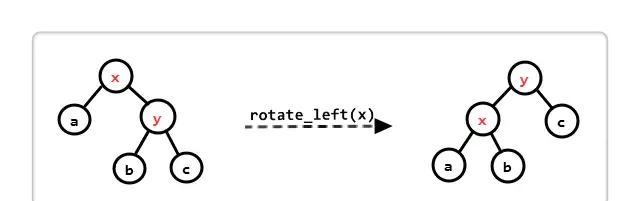
void RBTree::ratate_left(Node * x)
{
    Node * y = x->right;

    x->right = y->left;
    if (y->left)
        y->left->parent = x;
    y->parent = x->parent;

    if (x == root())
        root() = y;
    else if (x == x->parent->left)
        x->parent->left = y;
    else
        x->parent->right = y;

    y->left = x;
    x->parent = y;
}

右旋

void RBTree::rotate_right(Node * x)
{
    Node * y = x->left;

    x->left = y->right;
    if (y->right)
        y->right->parent = x;
    y->parent = x->parent;

    if (x == root())
        root() = y;
    else if (x == x->parent->right)
        x->parent->right = y;
    else
        x->parent->left = y;

    y->right = x;
    x->parent = y;
}

很容易看出，左旋和右旋其實就是兩個鏡像操作而已。

好了，真是千呼萬喚始出來，重點終于來了！

2.1 插入操作

将紅黑樹當作一顆二叉查找樹，将結點插入，插入後，該樹仍然是一棵二叉查找樹，但是它可能已經不是紅黑樹了，是以接下來就要通過 “旋轉” 和 “重新着色” 來使它重新成為紅黑樹。

首先，我們把新插入的結點着色為紅色。為什麼偏偏是紅色呢？先回顧下紅黑樹的四條性質：

每個結點要麼是紅的，要麼是黑的；
根結點是黑色的；
如果一個結點是紅色的，則它的兩個孩子都是黑色的；
對于任意一個結點，其到葉子結點的每條路徑上都包含相同數目的黑色結點。

将插入的結點着色為紅色，不會違背 “性質 4”。而少違背一條性質，就意味着我們需要處理的情況越少。

其次，我們再來看看插入結點會遇到哪幾種情況，分析發現，一共有三種：

被插入結點是根結點，那我們把此結點塗為黑色就行了；
被插入結點的父親結點是黑色的，那麼什麼也不需要做，結點被插入後，仍然是紅黑樹。
被插入結點的父親結點是紅色的，那麼此時是違背 “性質 3” 的。

最後，“被插入結點的父親結點是紅色的” 這種情況下，被插入結點是一定存在非空祖父（即父親的父親）結點的。那麼此時這種情況可以進一步再劃分為 6 種情況，因為涉及到鏡像操作，是以我們隻需了解其中一邊鏡像的 3 種情況即可（為友善叙述，我們把 “被插入結點” 稱為 “目前結點”，那麼 “目前結點” 的父親的父親就叫做 “祖父結點”，而 “祖父結點” 如果還有一個兒子的話，我們就稱其為 “叔叔結點”。）：

Case 1 ：目前結點的父親為紅色，叔叔存在且也是紅色

圖中，“結點 1” 為 “目前結點”。那麼我們的處理政策就是：

将 “父親結點” 改為黑色；

将 “叔叔結點” 改為黑色；

将 “祖父結點” 改為紅色；

将 “祖父結點” 設為 “目前結點”，繼續進行操作。

處理完後，圖中顯示的兩條路徑上，黑色結點數相同且和原圖數目一緻。

Case 2：目前結點的父親為紅色，叔叔不存在或為黑色，且目前結點是其父親的右孩子

圖中，“結點 2” 為 “目前結點”。那麼我們的處理政策就是：

将 “父親結點” 設為 “目前結點”；
以 “新的目前結點” 為支點進行左旋。

處理完後，我們發現依舊不滿足紅黑樹的性質，别急，這就是 “Case 3”。

Case 3：目前結點的父親為紅色，叔叔不存在或為黑色，且目前結點是其父親的左孩子

圖中，“結點 1” 為 “目前結點”。那麼我們的處理政策就是：

将 “父親結點” 改為黑色；
将 “祖父結點” 改為紅色；
以 “祖父結點” 為支點進行右旋。

處理完後，圖中顯示的兩條路徑上，黑色結點數相同且和原圖數目一緻。

2.2 删除操作

和删除一棵普通二叉查找樹的結點相同，我們會遇到三種情況：

“被删結點” 沒有孩子，那麼直接删除即可；
“被删結點” 隻有一個孩子，那麼直接删除該結點，并用該結點的唯一孩子替換它；
“被删結點” 有兩個孩子，那麼先找出它的 “後繼結點”，然後删除 “被删結點”，再用 “後繼結點” 去替換 “被删結點”。

為友善叙述，我們把 “被删結點” 稱為 “原先結點”，用來替換 “被删結點” 的結點稱為 “目前結點”。

首先，我們來看看删除一個結點會遇到哪幾種情況，分析發現，一共有四種：

“原先結點” 為黑色，“目前結點” 為紅色，那麼我們把 “原先結點” 删掉後，拿 “目前結點” 去替換它并修改顔色為黑色即可；.
“原先結點” 為黑色，“目前結點” 為黑色，這種情況比較複雜，待會再說；
“原先結點” 為紅色，“目前結點” 為紅色，那麼我們把 “原先結點” 删掉後，直接拿 “目前結點” 去替換它即可；
“原先結點” 為紅色，“目前結點” 為黑色，那麼我們把 “原先結點” 删掉後，再拿 “目前結點” 去替換它。我們發現，此時 “原先結點” 位置是滿足紅黑樹性質的，但是由于 “目前結點” 被拿走，“目前結點” 位置可能就會違背紅黑樹性質。分析發現，此時的 “目前結點” 不就是上面 “情況 1” 和 “情況 2” 中所講的 “原先結點”！那麼目前的這種情況直接就變成了 “情況 1” 或 “情況 2”。

最後，我們看下上述的 “情況 2”。這種情況可以進一步再劃分為 8 種情況，因為涉及到鏡像操作，是以我們隻需了解其中一邊鏡像的 4 種情況即可（注意，下面的圖檔上，“原先結點” 已被删除，故未畫出，我們隻畫出了 “目前結點”）：

Case 1：目前結點是黑色，兄弟結點是紅色

圖中，“結點 1” 為 “目前結點”。觀察上圖，因 “原先結點” 已被删除，故原來每條路徑上應該是 3 個黑色結點（右側路徑未畫完全），此時左側少了一個，那麼我們的處理政策就是：

将 “兄弟結點” 改為黑色；
将 “父親結點” 改為紅色；
以 “父親結點” 為支點進行左旋；
左旋後，重新設定 “兄弟結點”。

處理完後，我們發現最左側路徑依舊是 2 個黑色結點，說明目前狀态并不滿足紅黑樹性質。其實，這是進入了下面的 Case 2，Case 3，和 Case 4 階段了，請繼續往下看。

Case 2：目前結點是黑色，兄弟結點是黑色，兩個孩子為空或是黑色

圖中，“結點 1” 為 “目前結點”。觀察上圖，因 “原先結點” 已被删除，故原來每條路徑上應該是 2 個黑色結點，此時左側少了一個，那麼我們的處理政策就是：

将 “兄弟結點” 改為紅色；
将 “父親結點” 設定為新的 “目前結點”，繼續進行操作。

處理完後，我們發現圖中路徑都隻有 1 個黑色結點，說明目前狀态不滿足紅黑樹性質，但是我們發現隻要把 “結點 2” 着色為黑色不就行了麼，這也就是

erase_rebalance

代碼最後出現

if(x) x->color = black

;的緣由之一（x指向的是 “目前結點”）。

Case 3：目前結點是黑色，兄弟結點是黑色，兄弟結點的左孩子是紅色，右孩子是為空或是黑色

将 “兄弟結點” 的左孩子改為黑色；
将 “兄弟結點” 改為紅色；
以 “兄弟結點” 為支點進行右旋；
右旋後，重新設定 “目前結點” 的 “兄弟結點”。

處理完後，我們發現圖中最左路徑隻有 1 個黑色結點，說明目前狀态不滿足紅黑樹性質。其實這是進入了 Case 4。

Case 4：目前結點是黑色，兄弟結點是黑色，兄弟結點的右孩子是紅色，左孩子為空或紅黑皆可

将 “父親結點” 的顔色賦給 “兄弟結點”；
将 “父親結點” 改為黑色；
将 “兄弟結點” 的右孩子改為黑色；
以 “父親結點” 為支點進行左旋；

處理完後，一切 OK。

三：完整代碼

/**
*
* author 劉毅（Limer）
* date   2017-08-20
* mode   C++
*/
#include <iostream>
#include <algorithm>
using namespace std;

enum { red = 0, black = 1 };

struct Node
{
    int key;
    bool color;
    Node * parent;
    Node * left;
    Node * right;
    Node(int key = 0)
    {
        this->key = key;
        this->color = red;
        this->parent = this->left = this->right = nullptr;
    }
};

class RBTree
{
private:
    Node * header;
private:
    void ratate_left(Node * x);
    void rotate_right(Node * x);
    void destroy(Node * node);
    Node *& root();
    void insert_rebalance(Node * x);
    void erase_rebalance(Node * z);
    void in_order(Node * node);
public:
    RBTree();
    ~RBTree();
    Node * insert(int key);
    Node * find(int key);
    void erase(int key);
    void print();
};

void RBTree::ratate_left(Node * x)
{
    Node * y = x->right;

    x->right = y->left;
    if (y->left)
        y->left->parent = x;
    y->parent = x->parent;

    if (x == root())
        root() = y;
    else if (x == x->parent->left)
        x->parent->left = y;
    else
        x->parent->right = y;

    y->left = x;
    x->parent = y;
}

void RBTree::rotate_right(Node * x)
{
    Node * y = x->left;

    x->left = y->right;
    if (y->right)
        y->right->parent = x;
    y->parent = x->parent;

    if (x == root())
        root() = y;
    else if (x == x->parent->right)
        x->parent->right = y;
    else
        x->parent->left = y;

    y->right = x;
    x->parent = y;
}

void RBTree::destroy(Node * node)
{
    if (node == nullptr)
        return;
    destroy(node->left);
    destroy(node->right);
    delete node;
}

Node *& RBTree::root()
{
    return header->left;
}

void RBTree::insert_rebalance(Node * x)
{
    x->color = red;

    while (x != root() && x->parent->color == red)
    {
        if (x->parent == x->parent->parent->left)
        {
            Node * y = x->parent->parent->right;

            if (y && y->color == red)           // Case 1
            {
                x->parent->color = black;
                y->color = black;
                x->parent->parent->color = red;
                x = x->parent->parent;
            }
            else
            {
                if (x == x->parent->right)      // Case 2
                {
                    x = x->parent;
                    ratate_left(x);
                }

                x->parent->color = black;       // Case 3
                x->parent->parent->color = red;
                rotate_right(x->parent->parent);
            }
        }
        else  // same as above, just left <-> right
        {
            Node * y = x->parent->parent->left;

            if (y && y->color == red)
            {
                x->parent->color = black;
                y->color = black;
                x->parent->parent->color = red;
                x = x->parent->parent;
            }
            else
            {
                if (x == x->parent->left)
                {
                    x = x->parent;
                    rotate_right(x);
                }

                x->parent->color = black;
                x->parent->parent->color = red;
                ratate_left(x->parent->parent);
            }
        }
    }

    root()->color = black;  // Do not forget!
}

void RBTree::erase_rebalance(Node * z)
{
    Node * y = z;
    Node * x = nullptr;
    Node * x_parent = nullptr;

    if (y->left == nullptr)
        x = y->right;
    else if (y->right == nullptr)
        x = y->left;
    else
    {
        y = y->right;
        while (y->left)
            y = y->left;
        x = y->right;
    }  

    if (y != z)  // if y is z's successor
    {
        z->left->parent = y;
        y->left = z->left;
        if (y != z->right)
        {
            x_parent = y->parent;
            if (x)
                x->parent = y->parent;
            y->parent->left = x;
            y->right = z->right;
            z->right->parent = y;
        }
        else
            x_parent = y;

        if (root() == z)
            root() = y;
        else if (z->parent->left == z)
            z->parent->left = y;
        else
            z->parent->right = y;
        y->parent = z->parent;
        swap(y->color, z->color);
        y = z;
    }
    else
    {
        x_parent = y->parent;
        if (x)
            x->parent = y->parent;
        if (root() == z)
            root() = x;
        else if (z->parent->left == z)
            z->parent->left = x;
        else
            z->parent->right = x;
    }
    // now, y is pointing to what you will erase!
    //      x is the child of y, and note that x might be nullptr.



    // Now, the actual reblance is coming!
    // .....
    if (y->color == black)
    {
        while (x != root() && (x == nullptr || x->color == black))
        {
            if (x == x_parent->left)
            {
                Node * w = x_parent->right;
                if (w->color == red)                                      // Case 1
                {
                    w->color = black;
                    x_parent->color = red;
                    ratate_left(x_parent);
                    w = x_parent->right;
                }

                if ((w->left == nullptr || w->left->color == black) &&    // Case 2
                    (w->right == nullptr || w->right->color == black))
                {
                    w->color = red;
                    x = x_parent;
                    x_parent = x_parent->parent;
                }
                else
                {
                    if (w->right == nullptr || w->right->color == black)  //Case 3
                    {
                        if (w->left)
                            w->left->color = black;
                        w->color = red;
                        rotate_right(w);
                        w = x_parent->right;
                    }

                    w->color = x_parent->color;                           // Case 4
                    x_parent->color = black;
                    if (w->right)
                        w->right->color = black;
                    ratate_left(x_parent);
                    break;
                }
            }
            else  // same as above, just left <-> right
            {
                Node * w = x_parent->left;
                if (w->color == red)
                {
                    w->color = black;
                    x_parent->color = red;
                    rotate_right(x_parent);
                    w = x_parent->left;
                }

                if ((w->right == nullptr || w->right->color == black) &&
                    (w->left == nullptr || w->left->color == black))
                {
                    w->color = red;
                    x = x_parent;
                    x_parent = x_parent->parent;
                }
                else
                {
                    if (w->left == nullptr || w->left->color == black)
                    {
                        if (w->right)
                            w->right->color = black;
                        w->color = red;
                        ratate_left(w);
                        w = x_parent->left;
                    }

                    w->color = x_parent->color;
                    x_parent->color = black;
                    if (w->left)
                        w->left->color = black;
                    rotate_right(x_parent);
                    break;
                }
            }
        }

        if (x)
            x->color = black;
    }
}

void RBTree::in_order(Node * node)
{
    if (node == nullptr)
        return;

    in_order(node->left);
    cout << "( " << node->key << ", " << node->color << " )" << endl;
    in_order(node->right);
}

RBTree::RBTree()
{
    header = new Node(0);
}

RBTree::~RBTree()
{
    destroy(root());
    delete header;
    header = nullptr;
}

Node * RBTree::insert(int key)
{
    Node * cur = root();
    Node * pre = header;
    while (cur)
    {
        pre = cur;
        if (key < cur->key)
            cur = cur->left;
        else if (key > cur->key)
            cur = cur->right;
        else
            return nullptr;
    }

    cur = new Node(key);
    cur->parent = pre;
    if (pre == header || key < pre->key)
        pre->left = cur;
    else
        pre->right = cur;

    insert_rebalance(cur);
    return cur;
}

Node * RBTree::find(int key)
{
    Node * z = root();
    while (z)
    {
        if (key < z->key)
            z = z->left;
        else if (key > z->key)
            z = z->right;
        else
            return z;
    }
    return z;
}

void RBTree::erase(int key)
{
    Node * z = find(key);
    if (z)
    {
        erase_rebalance(z);
        delete z;
    }
}

void RBTree::print()
{
    in_order(root());
    cout << endl;
}

int main()
{
    RBTree rb_tree;

    // test "insert"
    rb_tree.insert(7);
    rb_tree.insert(2);
    rb_tree.insert(1); rb_tree.insert(1);
    rb_tree.insert(5);
    rb_tree.insert(3);
    rb_tree.insert(6);
    rb_tree.insert(4);
    rb_tree.insert(9);
    rb_tree.insert(8);
    rb_tree.insert(11); rb_tree.insert(11);
    rb_tree.insert(10);
    rb_tree.insert(12);
    rb_tree.print();

    // test "find"
    Node * p = nullptr;
    cout << ((p = rb_tree.find(2)) ? p->key : -1) << endl;
    cout << ((p = rb_tree.find(100)) ? p->key : -1) << endl << endl;

    // test "erase"
    rb_tree.erase(1);
    rb_tree.print();
    rb_tree.erase(9);
    rb_tree.print();
    rb_tree.erase(11);
    rb_tree.print();

    return 0;
}

資料測試如下圖：

紅黑樹還是很複雜的，是以建議讀者結合算法可視化工具來了解紅黑樹。注意，該平台的 “删除操作” 采用的是 “前驅替換原則”，這和本文的“後繼替換原則” 不同。

四：時間複雜度

最壞情況，輸入的序列為升序或降序，此時紅黑相間的路徑長度是全黑路徑長度的 2 倍，時間複雜度為 Oworst(2logn)。

紅黑樹具體實作與代碼分析

一：背景

二：具體實作與代碼分析

左旋

右旋

2.1 插入操作

2.2 删除操作

三：完整代碼

四：時間複雜度

繼續閱讀

swmm與lisflood-fp源碼如何一起編譯 CMake指令

CSMA/CD1． CSMA/CD的概述2． CSMA 的工作原理3． CSMA/CD控制規程及特點4． CSMA/CD協定5． CSMA/CD的優點6．結束語

Windows下VS開發環境環境安裝工程項目設定關于Debug和Release的提示

一文看懂字元串的加減乘除

極大似然法(ML)與最大期望法(EM)

C++ 第十五周報告1--《冒泡法排序》

C++實作簡單順序表

筆試面試題目：滑動視窗(二)

資料結構與算法（27）——排序（二）

Dijkstra--簡易版（最短路徑）

C經典書籍筆記——C陷阱與缺陷②(文法陷阱之優先級)一、錯誤案列二、優先級規律

GitHub連夜封殺！這份阿裡 10W 字内部 Java 字面試手冊到底有多強？

線性表之順序表的實作

C++判斷素數、求最大公約數代碼判斷一個數是否為素數求兩個數的最大公約數

SequoiaDB巨杉資料庫C++驅動概述

hdu7108哈希

紅黑樹 具體實作與代碼分析

一：背景

二：具體實作與代碼分析

左旋

右旋

2.1 插入操作

2.2 删除操作

三：完整代碼

四：時間複雜度

繼續閱讀

紅黑樹具體實作與代碼分析