圖分析算法,以圖論為驅動,進行算法優化,結合應用工程,業務形态研究,不同領域場景模拟不同網絡結構,通過自由刻畫網絡圖形關系,驗證結構合理性,如邊的有向和無向及權重,進而輔助分析圖形關系、圖結構分析、網絡結構分析等研究工作。
我們通過清林情報分析師的應用插件“圖分析”功能,通過算法計算圖形生成容易了解的圖形解釋22種圖算法。
1、最小生成樹(Minimum Spanning Tree):
Prim算法 、Kruskal算法、Sollin(Boruvka)算法
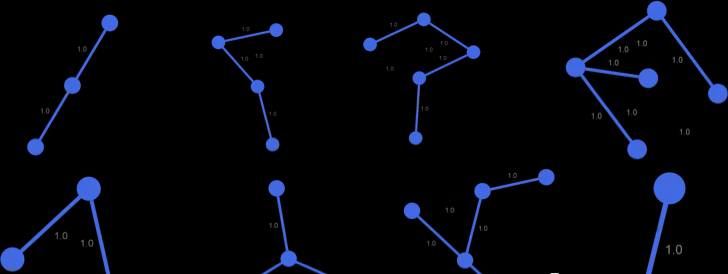
(1)Prim算法 ,普裡姆算法,圖論中的一種算法,基于一種貪心的思想,可在權重連通圖裡搜尋最小生成樹。意即由此算法搜尋到的邊子集所構成的樹中,不但包括了連通圖裡的所有頂點(英語:Vertex (graph theory)),且其所有邊的權值之和亦為最小。該算法于1930年由捷克數學家沃伊捷赫·亞爾尼克(英語:Vojtěch Jarník)發現;并在1957年由美國計算機科學家羅伯特·普裡姆(英語:Robert C. Prim)獨立發現;1959年,艾茲格·迪科斯徹再次發現了該算法。是以,在某些場合,普裡姆算法又被稱為DJP算法、亞爾尼克算法或普裡姆-亞爾尼克算法。Prime算法本質是動态規劃
(2)Kruskal算法,中文名克魯斯卡爾算法,本質是貪心算法,是求連通網的最小生成樹的另一種方法。與普裡姆算法不同,它的時間複雜度為O(eloge)(e為網中的邊數),是以,适合于求邊稀疏的網的最小生成樹。
(3)Sollin(Boruvka)算法,Sollin(Brouvka)算法雖然是最小生成樹最古老的一個算法之一,其實是前面介紹兩種算法的綜合,每次疊代同時擴充多顆子樹,直到得到最小生成樹T。
2、連通結構(Connected Components)
無向圖G的極大連通子圖稱為G的連通分量( Connected Component)。任何連通圖的連通分量隻有一個,即是其自身,非連通的無向圖有多個連通分量。這種結構稱作連通結構。
3、雙聯通結構(Biconnected Components)
任意兩點之間都有多于一條的路徑,則稱為雙連通圖,也叫雙連通分量,雙連通分量的術語是biconnected components,簡稱為BCC,這種結構為雙聯通結構。任何一對頂點之間至少存在有兩條路徑, 在删去某個頂點及與該頂點相關聯的邊時, 也不破壞圖的連通性。對于無向圖的一個子圖是雙連通的,則稱為雙連通子圖。極大的雙連通子圖稱為雙連通分量。一個無向圖可以有多個雙連通分量,一個點也算是雙連通分量。
4、強聯通結構(Strongly Connected Components)
有向圖的極大強連通子圖稱為的強連通分量,強連通圖隻有一個強連通分量,即是其自身。非強連通的有向圖有多個強連通分量。如果任意兩點之間都能到達,則稱為強連通圖。如果對于有向圖的一個子圖是強連通的,則稱為強連通子圖,這種結構稱為強聯通結構。
5、可達性(Reachability)
在圖論中,可達性是指在圖中從一個頂點到另一個頂點的容易程度。在無向圖中,可以通過識别圖的連接配接分量來确定所有頂點對之間的可達性。我們的産品解決方案,通過定義一個實體為原點,通過原點連結計算出圖中有向可達路徑範圍和無向可達路徑範圍,無向可達範圍一般大于有向可達。
常用算法為:Floyd-Warshall,Thorup,Kameda這三種算法。
(1)Floyd-Warshall算法
Floyd-Warshall算法(Floyd-Warshall algorithm)是解決任意兩點間的最短路徑的一種算法,可以正确處理有向圖或負權的最短路徑問題,同時也被用于計算有向圖的傳遞閉包。Floyd-Warshall算法的時間複雜度為O(N),空間複雜度為O(N*N)。
(2)Thorup 算法
對于平面有向圖,一種更快的方法是如Mikkel Thorup在2004年所提出的算法。計算複雜度為 ,其中為增長速度非常緩慢的inverse-Ackermann函數。該算法還可以提供近似最短路徑距離以及路由資訊。
(3)Kameda算法
如果圖形是平面的,非循環的,并且還表現出以下附加屬性,則可以使用由1975年的T.Kameda 提出的更快的預處理方法:所有0-indegree和所有0-outdegree頂點出現 (通常假設為外面),并且可以将該面的邊界分割為兩個部分,使得所有0個不等的頂點出現在一個部分上,并且所有的0度外的頂點出現在另一個部分上 (即兩種類型的頂點不交替)。
6、K核算法(K-Core)
k-Core算法是一種經典圖算法,用于尋找一個圖中符合指定核心度的頂點的集合,即要求每個頂點至少與該子圖中的其他k個頂點相關聯。k-Core算法用于尋找一個圖中符合指定核心度的頂點的集合,求每個頂點至少與該子圖中的其他k個頂點相關聯。這個我們提供1-5Core的圖計算,在圖譜中可以分别找出1-5Core的團結果發現,并可以用于子圖分類。适用于圖推演、生物學、社交網絡、金融風控等場景。
7、全路徑(All Paths)
全路徑,就是網絡圖中的路徑集合。分有向和無向,有向路徑通過源到目标方向不可逆,無向路徑通過源點和目标之間産生的圖關系。在同一圖形中,無向路徑遠多于有向。源點,是設定的初始點,目标是設定的需要通過源點要到達的點。有幾種基本情況,一是源點和目标點同一設定,即自循環,有向情況下,自循環就是1個節點。二是無向情況下,自循環和有向情況一樣,但二個節點以上則會多種混合循環體。産品可以通過設定源點和目标,進行分析源點和目标之間産生的有向無向關系。
8、鍊結構(ALL Chains)
鍊結構,包含循環或路徑,結構從圖形結構樹的基本循環集派生而來。通過優先搜尋圖形結構,把圖中鍊分解成一組循環或路徑,從原點出發有向或無向遠離根原點後又回到原點則為基本環。如果沒有回到原點則為一條路徑而不是一個環。每個循環或路徑稱為鍊。這種結構稱為鍊結構。
9、Single Source
Single Source,稱為單源,意為隻有一個源為基礎。首先是不允許有負環,單源實體到所有實體的最短路徑構成一棵最短路徑樹。通過單源路徑算法可以通過選中實體定義源,找出以這個實體源為中心或起始點的圖結果。
10、環結構(Cycles)
環結構,即網絡的循環結構,通過有向或無向路徑最後,形成回到起點閉環。可以了解為形成一個“圈”。網絡的基礎循環是循環的最小集合,使得網絡中的任何循環都可以寫成基礎中的循環總和。循環基數很有用,如單循環(自循環)、雙向循環(雙實體雙向關系)、三角循環(三個實體循環路徑)、四方循環(四個實體循環路徑)、五邊形以此類推。
11、度中心性(Degree Centrality)
(1)概念
這一概念起源于社會網絡研究。最初對社會網絡感興趣的是英國著名的人類學家布朗,他在對社會結構的關注中,以相對來說非技術的形式提出了“社會網絡”的思想。從20世紀30年代到70年代,越來越多的社會人類學家和社會學家開始建構布朗的“社會結構”和“社會網絡”概念,一些關鍵概念也應運而生,諸如“密度”、“中心度”、“三方關系”等概念如雨後春筍,紛紛湧現。其中,美國加州大學艾爾溫分校社會學系和數理行為科學研究所的研究教授林頓 C·弗裡曼于1979年在美國社會網絡雜志上發表《社會網絡中心度的概念說明》一文中正式提出了度中心性的概念。
(2)圖論
在圖論與網絡分析中,中心性是判定網絡中節點重要性的名額,是節點重要性的量化。這些中心性度量名額最初應用在社會網絡中,随後被推廣到其它類型網絡的分析中。在社會網絡中,一項基本任務是需要鑒定一群人中哪些人比其他人更具有影響力,幫助研究人員分析和了解扮演者在網絡中擔當的角色。為完成這種分析,這些人以及人與人之間的聯系被模型化成網絡圖,網絡圖中的節點代表人,節點之間的連邊表示人與人之間的聯系。基于建立起來的網絡結構圖,使用一系列中心性度量方法就可以計算出哪個個體比其他個體更重要。
(3)應用
度中心性,可以分為度中心度、度中心性及出度中心性。在一個有向圖中,我們可以有出度和入度的中心性二種衡量方式。在網絡中,一個節點的度越大,就意味着這個節點的度中心性就越高,就說明在網絡中這個節點越重要。主要應用與社會網絡分析、網絡使用者行為分析、信用網絡分析、圖論研究、複雜網絡研究,腦功能網絡分析、欺詐網絡分析等場景。
12、重心(Weight Centrality)
重心,即權重中心性。每個實體節點為頂點,而實體節點之間的關系邊。實體節點之間的互相作用是形成邊權重。每個頂點的關聯邊數越多邊權重占每個獨立圖中權重就越大。
13、圖中心(Graph Centrality)
圖中心,圖中最強中心性的一個或多個實體節點,一個圖中心,實體節點權重最大且唯一,多個圖中心,在有向圖中,二個以上實體節點在圖中權重值相同且權重值相同。圖中中心性用實體大小、顔色深淺進行區分,最高權重實體節點實體越大顔色最深,低權重或中心性低的實體節點則相反。
14、中介中心性(Node Edge Betweeness Centrality)
中介中心性,又叫中間中心性,中間性,居間中心性等等。主要計算實體節點在圖中的中間性。以經過某個節點的最短路徑數目來刻畫節點的重要性名額。對于權重圖,邊權重必須大于零。零邊權重可以在節點對之間産生無限數量的等長路徑。對于有向圖和無向圖,源圖(實體節點或實體節點關系集合)和目标之間的路徑總數的計數方式不同。有向路徑很容易計算。如果實體節點子集和目标子集相同,則我們要對無向路徑進行計算。
15、近親中心性(Closeness Centrality)
近親中心性,又稱接近度中心性,通過計算圖網絡中每個實體節點的接近程度。通過各實體節點的接近度在圖中可良好比對呈現,接近度的中心性被歸一化,每個實體節點的在本圖網絡中的中心分布。計算出每個實體節點所在位置連結部分的中心度。如果圖形中的未完全連結的子網絡,則計算按該子網絡大小單獨縮放的每個已連接配接實體節點或實體子網絡的接近度中心性。
16、特征向量中心性(Eigenvector Centrality)
一個節點的重要性即取決于其鄰居節點的數量(即該節點的度),也取決與每個鄰居節點的重要性。與之相連的鄰居節點越重要,則該節點就越重要。
17、Page Rank
PageRank,Google的網頁排序算法,又稱網頁排名、谷歌左側排名,是一種由搜尋引擎根據網頁之間互相的超連結計算的技術,而作為網頁排名的要素之一,谷歌的兩位創始人,拉裡·佩奇 (Larry Page) 和爾蓋·布林 (Sergey Brin) 對網頁排序問題進行研究。後來以拉裡·佩奇(Larry Page)之姓來命名。Google用它來展現網頁的相關性和重要性,在搜尋引擎優化操作中是經常被用來評估網頁優化的成效因素之一。當初主要是為了用來評估構成網絡中的每一個節點的重要性。
18、鍊子結構(Chains)
鍊子結構,即鍊圖中的獨立子鍊結構,需要三個或以上實體節點,二個或以上邊的條件形成。實體節點通過邊形成有向或無向的鍊結構且無環路結構。有向鍊中方向流向一緻。
19、環子結構(Cycles)
環子結構,即圖中的獨立子環結構,需要三個或以上實體節點,二個或以上邊的條件形成。實體節點通過邊形成有向或無向的環形子結構,且整個子結構的環中的環外連結有唯一實體節點連結,且連結唯一。
20、星型子結構(Stars)
星型子結構,是星型結構中包含至少一個子結構。星型結構以實體節點為中心,并用單獨的線路使這個中心實體節點與其他各節點相連,相鄰節點之間的連結都要通過中心節點,相當于單層結構。星型子結構包含最小獨立星型和網絡圖中的星型子結構,最小獨立星型即無向圖三個實體節點形成的鍊,有向圖三個實體節點形成方向向外的鍊,子結構,在圖中的一個頂點為中心的邊點連結形成星型結構,有向圖方向有連結,但不包含這個連結,關聯實體連結直接關聯二條以上向外方向的邊點結構的圖結構,無向圖符合基礎結構。且子結構上不包含其他邊點。
21、樹狀子結構(Trees)
樹狀子結構,是圖中的樹形結構,樹形結構是一層次的嵌套結構。一個樹形結構的外層和内層有相似的結構, 是以這種結構多可以遞歸的表示。樹形結構是一層次的嵌套結構。一個樹形結構的外層和内層有相似的結構, 是以這種結構多可以遞歸的表示。樹狀子結構和星型子結構類似,但樹狀子結構是多層的,星型子結構相當于單層結構,在圖中像樹杈一樣可以不斷向外擴散。