引言
相信大家都聽說過程式的本質就是算法加資料結構的說法,是以如果我們想程式跑的速度既快又非常節省資源。那麼就需要好好設計程式的執行算法以及資料結構。這就涉及到一個問題,我們在寫代碼的時候怎麼去評判一段代碼到底是不是跑得快又省資源的呢?這個時候我們就需要借助于時間複雜度以及空間複雜度分析來進行分析了。
碼代碼為什麼要進行複雜度分析?
有的同學會說,代碼能夠跑出結果實作功能不就行了嘛,為什麼還要進行複雜度分析呢?實際上代碼能實作指定的功能,是對程式的最低的要求。無論是我們平常的算法刷題或者實際項目中,都需要對于具體的代碼的執行性能有一定的要求,希望代碼能夠實作既能跑的快,又節省硬體資源,實作最優處理。
實際上我們可以通過一些工具、資料以及環境來進行程式的複雜度分析,包括耗時以及資源占用情況。但是這種評價方法依賴于準備的測試資料以及測試環境,不同規模的測試資料以及不同配置的測試環境,得到的測試結果具有不确定性。是以我們需要一種大緻的估算方法,在代碼寫出來之後可以粗略的估算代碼的複雜度,這樣有助于我們及時的調整代碼結構或者資料存儲結構。這個粗略的程式複雜度估算方法就是我們今天所要介紹的時間複雜度分析法以及空間複雜度分析法。
Big O複雜度表示法
在介紹時間複雜度以及空間複雜度之前,我們先來看下Big O複雜度表示法。還記得第一次基礎到Big O表示法是在網易公開課上的MIT算法導論課程上,感興趣的同學可以去看下。
假設有這樣的定義
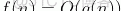
,存在常數c、以及
,使得
。舉個栗子,
,這其中實際上就是一種漸進的趨向,是以忽略了常數項。
上面闡述了對于Big O的數學定義,接下來我們就看下在代碼方面是符合進行使用的。假設有如下的代碼:
1 public static int calculator(int n) {
2 int sum = 0;
3 for (int i = 1; i <= n; ++i) {
4 for (int j = 1; j <= n; ++j) {
5 sum = sum + j;
6 }
7 }
8 return sum;
9 } 這段代碼很簡單,主要實作的了數字累加,這裡我們假設每行代碼執行的時間都時一個固定值為一個execution_time。那麼上面的代碼我們可以看出,第2行以及第8行代碼分别執行了一個execution_time,而第3行代碼由于在循環體中,是以執行了n個execution_time。另外第4行代碼以及第5行代碼分别執行了
次,是以這段代碼總的執行時間就是
個execution_time。
可以看得出來代碼的執行時間和實際的代碼的執行次數是成正比的。結合上文中的對于Big O的公式,可以得出代碼的時間複雜度表達式即為:
,其中n就表示為資料的規模,而T即為代碼的執行時間,而O就表示一種漸進的關系。相信大家都學過微積分,其中的很重要的思想就是無限趨近後用主要公式項,代替次要公式項。是以此處的常數項、低階項在n無窮大的時候都可以忽略掉。是以這段代碼的時間複雜度我們可以認為為
。
時間複雜度分析
從上文的分析中,我們學會了如何使用Big O表示法來分析代碼的的時間複雜度。上文中的例子隻是常見的一種,接下來我們再看看其他幾種常見的代碼結構如何進行是時間複雜度分析以及一些複雜度分析技巧。
1、O(1)
首先确認下O(1)表達的意思是并不是說代碼的執行時間複雜度為1,而是說代碼執行的時間複雜度是常數項。如下的代碼,按照上文分析的,每次執行代碼就是就是1個execution_time,那麼三行代碼就是3個execution_time,對應的時間複雜度是O(1),并不是O(3)。
1 int a = 1;
2 int b = 2;
3 int result = a * b; 是以代碼的時間複雜度并不與資料規模n正相關,即便是有1W行代碼,它的時間複雜度也還是O(1)。
2、O(n)
在如下的代碼中,随着n的增大,對應的3、4行代碼的執行次數也随着逐漸增大。借助于Big O表示法,我們可以分析出該段代碼的時間複雜度為
,其中第2、6行代碼執行實際為常數項,随着資料規模的增大,對最終結果的影響逐漸減小。是以我們在分析代碼時間複雜度的時候,重點關注影響因子最大的代碼塊,此處循環體就是影響因子最大的代碼塊。
1 public static int calculator(int n) {
2 int sum = 0;
3 for (int i = 1; i <= n; ++i) {
4 sum = sum + i;
5 }
6 return sum;
7 } 3、O(n²)
如上文Big O表示法中的分析可知,以下代碼的總的執行時間為(2n²+n+2)個execution_time,但是最後得出的時間複雜度為O(n²)。是以在此處我們也要說明下分析技巧,實際上還是使用的微積分的思想,當n趨近無窮大的時候,參數項、低階項n以及常數項2在n²面前都是弟弟,是以n²是這段代碼最耗時的部分,也就是說我們根據代碼分析時間複雜度的時候應該抓大放小,重點關注那些循環次數多的代碼塊,然後運用趨近無窮大的方法,确定最終的時間複雜度。
public static int calculator(int n) {
int sum = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
sum = sum + j;
}
}
return sum;
} 4、O(logn)
這類時間複雜度還是比較常見的,我們還是先來看下代碼:
1 public static int calculator(int n) {
2 i=1;
3 while (i <= n) {
4 i = i * 2;
5 }
6 return i;
7 } 我們可以很明顯的看出來,第4行代碼執行的次數最多,是以我們得先搞清楚這裡的代碼到底執行了多少次,我們才能确定這段代碼的時間複雜度。實際上它是個等比數列,我們都知道如果想擷取執行次數x,我們隻需要進行取對處理就可以。
是以此處的x=log2n,那麼該段代碼的時間複雜度就為O(log2n),在之前的大O表示法中,我們知道常數項是可以忽略掉的,是以代碼的複雜度實際就是O(logn)。
空間複雜度分析
在前文中,我們分析了代碼如何通過Big O表示法來确定時間複雜度。接下來我們再看看空間複雜度是怎樣的分析的,實際上空間複雜度分析主要考慮的是代碼實作所需要的空間規模與資料規模之間的趨勢關系。看下如下的代碼:
1 public static void save(int n) {
2 Set<Integer> ds = new HashSet<>(n);
3 for (int i = 0; i < n; i++) {
4 ds.add(i)
5 }
6 } 上述代碼中,在代碼的第二行申請了大小為n的set集合,其他代碼并沒有再申請新的存儲空間,是以這段代碼的空間複雜度就是O(n)。相對于時間複雜度來說,空間複雜度相對來說沒有太多的分類,分析的規則實際和時間複雜度優點類似,隻不過空間複雜度關注有沒有新的存儲空間申請。同樣的,空間複雜度分析也遵循抓大放小的原則,關注趨近無窮大的時候,真正起作用的因子。
總結
本文主要對于為什麼要對程式進行複雜度分析以及如何對程式進行時間複雜度分析和空間複雜度分析,這也是我們在寫出代碼後如何評價代碼是否執行高效的評價基礎。實際上我們常見的複雜度也就是O(1)、O(logn)、O(n)、O(nlogn)、O(n²),他們的複雜度依次從小到大。