對于一個序列建立的笛卡爾樹滿足:
- 它是個二叉樹。
- 若以下标為關鍵字,笛卡爾樹滿足二叉搜尋樹性質(若以每個點一下都包含一段連續的區間)。
- 若以權值為關鍵字,它是一個小根堆。
- 若權值互不相同,那麼這個序列的笛卡爾樹唯一(當然,若權值相同,就會有很多棵樹,于是就有笛卡爾樹計數啦)。
它具有這麼多優秀的性質,當然可以幹很多事情啦。
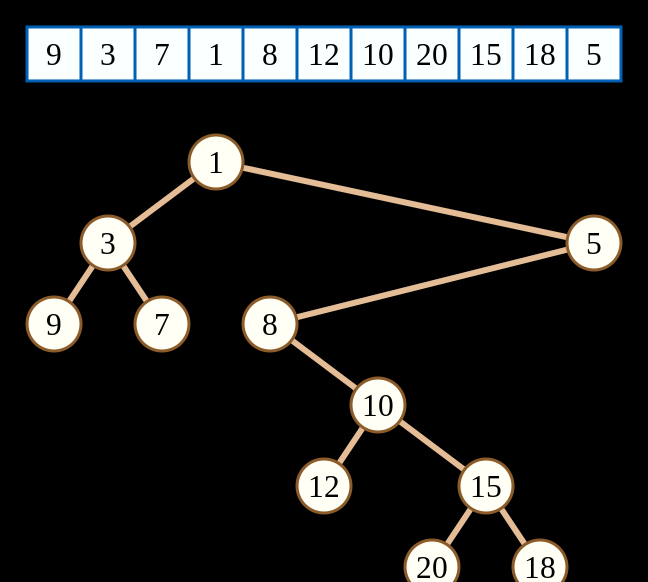
(以上圖檔來自維基百科)
建立
維護一個棧維護從隊列第一個元素到現在的遞增子序列(存的當然是下标),接下來分類讨論:
- 若新增元素大于等于棧頂,那麼直接進棧并與接到此時棧頂右兒子。
- 否則一直彈棧直到小于棧頂,将最後彈出的元素連到目前元素的左兒子,之後進站并連邊棧頂。
sta[rt=tp=1]=1;
for(int i=2;i<=n;i++)
{
if(a[i]>=a[sta[tp]]) ch[sta[tp]][1]=i,sta[++tp]=i;
else
{
while(a[i]<a[sta[tp]]) tp--;
if(!tp) rt=i;
ch[i][0]=sta[tp+1];
ch[sta[tp]][1]=i;
sta[++tp]=i;
}
}
笛卡爾樹計數
笛卡爾樹滿足根節點的的權值小于等于兒子節點的權值。
那麼對于給定的一個數列,這個序列中所有的最小值一定都直接連接配接在根節點上。
設有 \(m\) 個最小值,則這些節點可以組成的二叉樹個數……
就是卡特蘭數的第 \(m\) 項啦!
如上圖,将最小值提取出後,可以将原序列分成若幹段,分别求解最小值即可。
$\texttt{code}$
#define Maxn 1000005
#define Maxpown 21
#define mod 1000000007
typedef long long ll;
inline int rd()
{
int x=0;
char ch,t=0;
while(!isdigit(ch = getchar())) t|=ch=='-';
while(isdigit(ch)) x=x*10+(ch^48),ch=getchar();
return x=t?-x:x;
}
int n;
int st[Maxn][Maxpown],pos[Maxn][Maxpown];
int pow2[Maxpown],lg[Maxn];
ll Cart[Maxn],inv[Maxn<<1],mi[Maxn<<1],invmi[Maxn<<1];
inline ll C(int x,int y) { return mi[x]*invmi[x-y]%mod*invmi[y]%mod; }
inline ll ksm(ll x,ll y)
{
ll ret=1;
while(y)
{
if(y&1) ret=ret*x%mod;
x=x*x%mod,y>>=1;
}
return ret;
}
inline int query_pos(int l,int r)
{
int p=lg[r-l+1]-1;
if(st[l][p]<=st[r-pow2[p]+1][p]) return pos[l][p];
return pos[r-pow2[p]+1][p];
}
inline int query_min(int l,int r)
{
int p=lg[r-l+1]-1;
return min(st[l][p],st[r-pow2[p]+1][p]);
}
ll Find(int l,int r)
{
if(l>r) return 1;
ll ret=1;
int Last=l,fir,cnt=0,Least=query_min(l,r),Now;
while(Last<=r)
{
Now=query_min(Last,r);
if(Now>Least) { ret=ret*Find(Last,r); break; }
fir=query_pos(Last,r);
ret=ret*Find(Last,fir-1)%mod;
Last=fir+1,cnt++;
}
ret=ret*Cart[cnt]%mod;
return ret;
}
int main()
{
n=rd(),pow2[0]=1;
for(int i=1;i<=n;i++) st[i][0]=rd(),pos[i][0]=i;
inv[0]=mi[0]=invmi[0]=inv[1]=mi[1]=invmi[1]=1;
for(ll i=2;i<=n+n;i++)
{
mi[i]=mi[i-1]*i%mod;
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
invmi[i]=invmi[i-1]*inv[i]%mod;
}
for(int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
for(ll i=1;i<=n;i++) Cart[i]=C(i+i,i)*ksm(i+1,mod-2)%mod;
for(int i=1;i<=20;i++) pow2[i]=pow2[i-1]*2;
for(int i=1;i<=20;i++)
for(int j=1;j<=n-pow2[i]+1;j++)
{
if(st[j][i-1]<=st[j+pow2[i-1]][i-1])
pos[j][i]=pos[j][i-1];
else pos[j][i]=pos[j+pow2[i-1]][i-1];
st[j][i]=min(st[j][i-1],st[j+pow2[i-1]][i-1]);
}
printf("%lld\n",Find(1,n));
return 0;
}
直方圖最大子矩形
$\texttt{code}$
#define Maxn 100005
int n,tp,rt;
ll ans;
int a[Maxn],siz[Maxn],sta[Maxn];
int ch[Maxn][2];
inline void build()
{
sta[rt=tp=1]=1,ans=0;
for(int i=2;i<=n;i++)
{
if(a[i]>=a[sta[tp]]) ch[sta[tp]][1]=i,sta[++tp]=i;
else
{
while(a[i]<a[sta[tp]]) tp--;
if(!tp) rt=i;
ch[i][0]=sta[tp+1];
ch[sta[tp]][1]=i;
sta[++tp]=i;
}
}
}
void dfs(int x)
{
siz[x]=1;
for(int i=0;i<2;i++) if(ch[x][i])
dfs(ch[x][i]),siz[x]+=siz[ch[x][i]];
ans=maxll(ans,1ll*a[x]*siz[x]);
}
int main()
{
while((n=rd())!=0)
{
for(int i=1;i<=n;i++) a[i]=rd(),ch[i][0]=ch[i][1]=0;
build(),dfs(rt);
printf("%lld\n",ans);
}
return 0;
}