堆的定義
- 一個完全二叉樹中,任意父結點總是大于或等于(小于或等于)任何一個子節點,則為大頂堆(小頂堆)。
堆的數組存儲方式
完全二叉樹适合采用順序存儲的方式,是以一個數組可以看成一個完全二叉樹。
- 節點編号:樹根起,自上層到下層,每層從左至右,給所有結點順序編号,能得到一個反映整個二叉樹結構的線性序列。
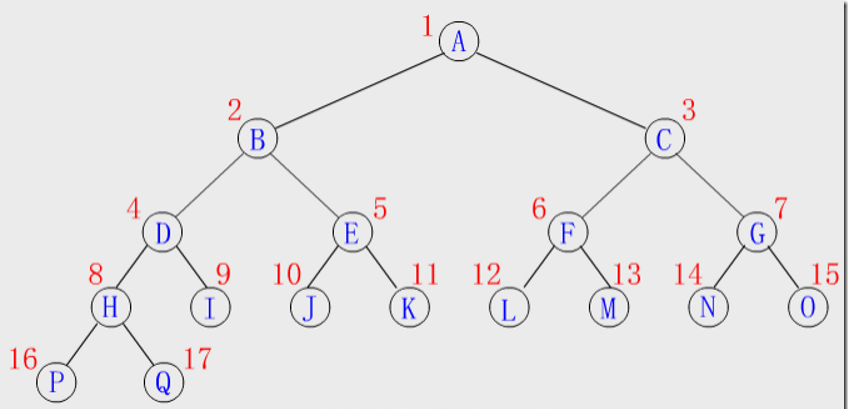
- 編号特點:
從一個結點的編号就可推得其雙親,左、右孩子,兄弟等結點的編号。假設編号為i的結點是ki(1≤i≤n),則有:
①若i>1,則ki的雙親編号為i/2;若i=1,則Ki是根結點,無雙親。
②若2i≤n,則Ki的左孩子的編号是2i;否則,Ki無左孩子,即Ki必定是葉子。是以完全二叉樹中編号i>n/2的結點必定是葉結點。
③若2i+1≤n,則Ki的右孩子的編号是2i+1;否則,Ki無右孩子。
注:ki(0≤i≤n)滿足數組下标時,則可能的左右孩子分别為2i+1、2i+2。
堆排序的思想(以大頂堆為例)
利用堆頂記錄的是最大關鍵字這一特性,每一輪取堆頂元素放入有序區,就類似選擇排序每一輪選擇一個最大值放入有序區,可以把堆排序看成是選擇排序的改進。
- 将初始待排序關鍵字序列(R0,R1,R2....Rn)建構成大頂堆,此堆為初始的無序區;
- 将堆頂元素R[0]與最後一個元素R[n]交換,此時得到新的無序區(R0,R1,R2,......Rn-1)和新的有序區(Rn);
- 由于交換後新的堆頂R[0]可能違反堆的性質,是以需要對目前無序區(R0,R1,R2,......Rn-1)調整為新堆。
不斷重複此2、3步驟直到有序區的元素個數為n-1,則整個排序過程完成。
篩選算法
//最難了解的地方
- 目标:一個所有子樹都為堆的完全二叉樹。意思就是這個二叉樹隻差跟節點不滿足堆的結構。//很重要,很重要,很重要
如下圖:
- 方法:首先将root和它的左右子樹的根結點進行比較,把最大的元素交換到root節點;然後順着被破壞的路徑一路調整下去,直至葉子結點,就得到新的堆。
- 運用:1.在上文提到的堆排序思想,2-3步驟中将無序區調整為堆的時候用到。
2.初始化堆
初始化堆
從最後一個非葉子節點i(i=n/2,n為節點個數)開始,将以i為根節點的二叉樹通過篩選調整為堆。以第一張圖為例,編号順序為8、7、6...1。
從最後一個非葉子節就保證了篩選算法的正确性,因為篩選算法的目标是一個所有子樹都為堆的完全二叉樹。
java實作堆排序
package sort;
import java.util.Arrays;
import util.MathUtil;
/**
* 通過大頂堆實作堆排序,升序排序
*
*/
public class HeapSort {
public static void main(String[] args) {
int[] arr={9,6,12,32,23,11,2,100,85};
sort(arr);
System.out.println(Arrays.toString(arr));
}
//這裡将i定義為完全二叉樹的根
//将完全二叉樹調整為大頂堆,前提是二叉樹的根的子樹已經為大頂堆。
public static void adjustHeap(int[]a ,int i,int size){
int lChild=2*i+1; //左孩子
int rChild=2*i+2; //又孩子
int max=i; //臨時變量
if(i<size/2){ //如果i是葉子節點就結束
if(lChild<size&&a[max]<a[lChild])
max=lChild;
if(rChild<size&&a[max]<a[rChild])
max=rChild;
if(max!=i){
MathUtil.swap(a, max, i);//交換後破環了子樹的堆結構
adjustHeap(a, max, size);//遞歸,調節子樹為堆
}
}
}
//建立堆,堆是從下往上建立的,因為adjustHeap函數是建立在子樹已經為大頂堆。
public static void buildHeap(int[]a,int size){
for(int i=size/2;i>=0;i--){//從最後一個非葉子節點,才能構成adjustHeap操作的目标二叉樹
adjustHeap(a, i, size);
}
}
//将數組分為兩部分,一部分為有序區,在數組末尾,另一部分為無序區。堆屬于無序區
public static void sort(int[] arr){
int size=arr.length;
buildHeap(arr, size);
for(int i=size-1;i>0;i--){//i為無序區的長度,經過如下兩步,長度遞減
//堆頂即下标為0的元素
MathUtil.swap(arr, i, 0);//1.每次将堆頂元素和無序區最後一個元素交換,即将無序區最大的元素放入有序區
adjustHeap(arr, 0, i); //2.将無順區調整為大頂堆,即選擇出最大的元素。
}
}
}