Deep Learning and Shallow Learning

由于 Deep Learning 現在如火如荼的勢頭，在各種領域逐漸占據 state-of-the-art 的地位，上個學期在一門課的 project 中見識過了 deep learning 的效果，最近在做一個東西的時候模型上遇到一點瓶頸于是終于決定也來了解一下這個魔幻的領域。

據說 Deep Learning 的 break through 大概可以從 Hinton 在 2006 年提出的用于訓練 Deep Belief Network (DBN) 的算法開始，打破了持續了數十年的多層神經網絡效果很差的尴尬局面，其之後各種其他的算法和模型也相繼被提出來并在各個應用領域中大展神威。而近來 Google 聘請 Hinton、紐約時報的封面報道等公衆媒體的宣傳，更是使得 deep learning 變得大紅大紫。記得之前在老闆的某個 draft 中看到過這樣一段話：

I do not expect that this paper will ever be published in the usual journals. “Success” for a paper published in this way would consist, I believe, of making an impact – measured in terms of citations for instance – and perhaps of being eventually “reviewed” in sites such as Wired or Slashdot or Facebook or even in a News and Views-type article in traditional journals like Science or Nature.

在學術界也是，比如在各個應用領域裡，Automatic Speech Recognition (ASR) 中不僅 deep learning 超越了傳統的 state-of-the-art 算法，而且超越程度之大使得 ASR 領域本身迎來了一次新的 break through​​(Hinton et al., 2012)​​；Collaborative Filtering 裡，Deep Learning 在 Netflix 最後獲獎算法中​​占據重要地位​​；Computer Vision (CV) 裡除了在各種大型 benchmark 資料庫上得到超越 state-of-the-art 結果（例如​​(Krizhevsky, Sutskever, & Hinton, 2012)​​）之外，據說 Google 也在它的圖像搜尋中開始使用 Deep Learning；NLP 領域我不是很了解，不過從這個 ​​Deep Learning for NLP (without Magic)​​ 的 Tutorial 來看，Deep Learning 在 NLP 裡也取得了相當的成功。甚至連純機器學習理論的會 COLT 也​​開始湊這趟熱鬧​​了。​​deeplearning.net​​ 上有一個 reading list，裡面列舉了一些各個領域關于 deep learning 的代表性文章。從 2013 年開始，deep learning 甚至有了自己專門的會：​​International Conference on Learning Representations (ICLR)​​。

從會議的名字也可以看出，deep learning 其實很重要的一點就是得到好的 representation，各種實驗表明，通過 deep learning 的出來的網絡，即使把最上層的分類/回歸模型丢掉，直接把網絡當做一個 feature extractor，把抽出來的特征丢到普通的 SVM 之類的分類器裡，也經常會得到性能提高。雖然從資訊論的角度來說，由于 ​​Data Processing Inequality​​ 導緻 feature extraction 并不會在“資訊量”上帶來什麼改善，但是從 practical 的角度來說，一個好的 representation 無疑是非常重要的。關于這一點，我最近聽說了一個非常形象的例子：有人在抱怨乘法比加法難算好多，比如 9480208 和 302842 的和，隻要各位對齊，一位一位地加并處理好進位就好了，即使連我這樣的渣口算能力估計都沒問題；但是如果是乘法的話……但是其實這裡的難易程度是由于我們常用的數字的十進制表達偏向于加法計算的緣故。如果我們換一種表達：每一個數字可以等價地表達為它的素數因子的集合，例如

那麼兩個數相乘就再簡單不過了：

反過來在這種 representation 下做加法就很困難了。基于同樣的原因，representation 的問題在機器學習以及相關領域中一直是一個非常重要的研究課題。因為不同的問題、不同的資料和不同的模型，合适的 representation 可能會很不一樣，而找到正确的 representation 之後往往就可以事半功倍。

圖 1

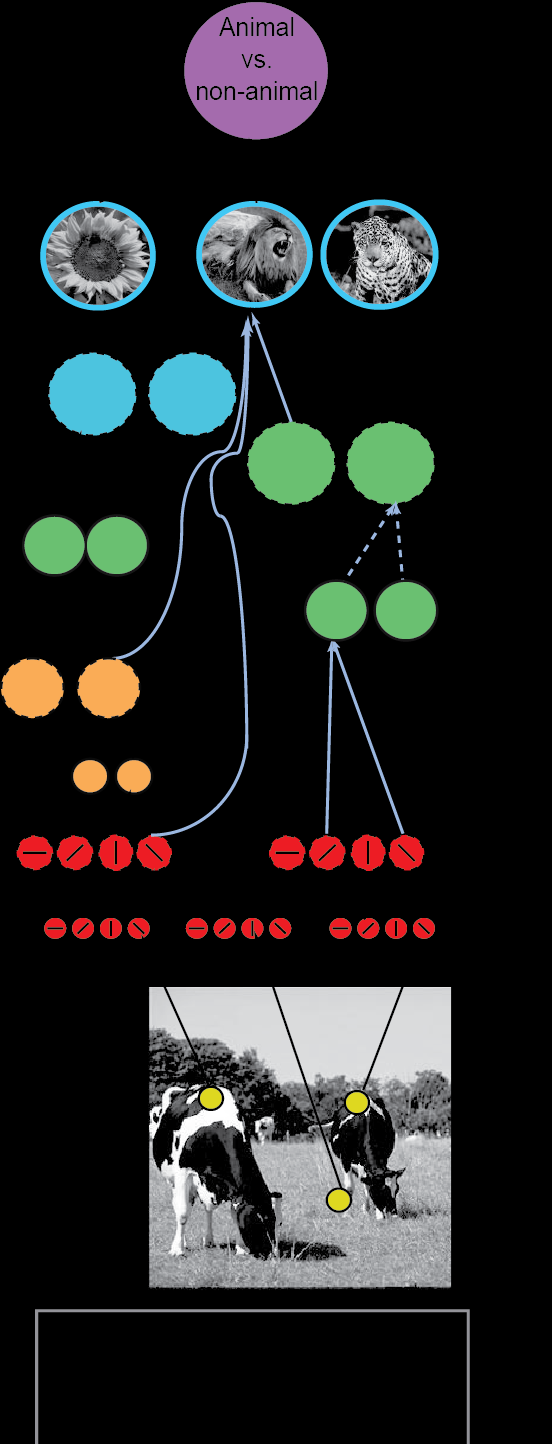
HMAX。Convolutional feedforward object recognition models inspired by the primate ventral visual pathway.

在特定的問題中，一般采集到資料之後會進行一些特征提取的處理，例如 Vision 裡的 SIFT + Bag of Words，或者 Speech 裡的 MFCC 之類的特征，這些特征提取的算法往往都是人們根據該問題資料的特征人工設計出來的，并且一直以來設計更好的 feature 實際上在各個領域裡也是非常重要的研究問題。而現在 deep learning 的結果展示比較喜歡做的一件事情就是從“原始資料”（比如 Vision 裡的像素 bitmap）出發自動學習 representation，并給出比之前精心設計的人工 feature 的效果還要好。不過我覺得這也并不代表說 deep learning 就在這裡是萬能的，因為一方面能夠有效地結合已知的領域内的 domain knowledge 實際上是非常重要的一個特性，另一方面，deep network 也并不是像一個 black box 一樣直接把 raw data 丢過去它就能 magically 給出像樣的特征來。deep model 訓練困難似乎算是得到公認的了；并且比如像 convolutional neural network (CNN) 這樣的模型其網絡結構本身就是根據 underlying data 本身所要求的 invariance 特性而人工設計的；再比如像在 speech 裡目前效果最好的做法似乎也還是在基于 speech data 的各種經典處理工序之後得到的 Mel Frequency Filter Bank 資料上而不是最原始的聲音波形上做 deep learning。

除了手工特征提取之外，deep learning 之前也有許多其他所謂“shallow”的 data-driven 的特征提取的算法。最經典的 PCA 降維可以從去除噪音等等各個方面來進行解釋。像生物的 microarray 之類的資料上，每個樣本點的次元非常高，同時由于采集樣本的成本高昂，導緻樣本的數量有非常低，是以各種各樣的降維或者特征選擇的方法湧現出來，以限制模型的複雜度，避免在小樣本資料上出現嚴重的過拟合問題。

世界的另一頭，是資料如白菜一樣便宜的“big data”時代，樣本的充裕（和計算機性能的提升）使得訓練更加複雜的模型成為可能，是以反過來又“升維”以獲得更豐富的資料表達，這裡 Kernel Method 是一個經典的工具。核方法的基本思路是通過一個正定核  誘導出來的線性映射  将資料映射到一個 Reproducing Kernel Hilbert Space (RKHS) 中，然後使用 RKHS 中的線性模型來處理資料。

這裡的  就相當于是一個非線性的特征抽取的過程。一方面，通過核函數可以有效地在原始的資料空間次元的複雜度下面對映射過後的特征空間中的點進行（内積）計算；另一方面，諸如像高斯核之類的核函數對應的特征空間實際上是無限維空間，可以說有相當大的自由度。此外，核方法還是 non-parametric 的，也就是說，并不需要假設 target hypothesis  是某種形式的函數，而是可以在整個 RKHS  中尋找最接近  的函數，然後通過 Representer Theorem 可以把這些優化函數轉換為有限維空間上的優化問題，最終的近似 target  也變成了由核函數在訓練資料上所“Interpolate”成的函數：

是以說從某種意義上來說，核方法似乎并不是在使用整個 ，而隻是在用一個由訓練資料映射後的  張成的子空間在做近似。由于 Representer Theorem 實際上是保證在整個  中優化和在這個子空間中優化的最優解是一樣的，是以這裡的局限性其實并不是來自于 Kernel Method，而是來自于使用有限的訓練資料通過 Empirical Risk Minimization 去近似 Risk Minimization 的時候造成的問題。另外，核方法在 learning theory 方面也有非常多的研究和結論。雖然到目前為止 Machine Learning Theory 裡的 Theoretical Bounds 很少有可以用來實際直接指導具體問題中的諸如參數選擇之類的事情，但是理論上的研究工作仍然是不能忽視的。

核方法的工作原理有一個比較粗糙的直覺解釋，考慮最常用的高斯核 ，其中  是核的參數。對于一個特定的點  來說，取決于實作給定的  的大小，在一定半徑範圍之外的資料點 ， 的值基本上就可以小到可以忽略不計了。是以  的線性組合其實隻是在  點的周圍一個 local neighborhood 裡求和。

圖 2

核方法通過 local neighbors 進行插值計算。

也就是說，可以近似地看成是在每一個 local neighborhood 裡進行局部的線性回歸，同時又全局地限制重疊的那些 local neighborhood 所對應的線性回歸的重疊的系數必須要相等，可能還有一些全局的 regularization 之類的。如果一個函數比較光滑，或者我們的資料點足夠密集，而核函數的  又選得比較好使得 local neighborhood 大小比較合适的話，函數通常在每個點的局部領域裡都能很好地通過線性函數來進行近似。

不過，看似優良的性質同時也受到了質疑 ​​(Bengio, Delalleau, & Roux, 2005)​​，因為如果在訓練資料 cover 比較少的區域的話，似乎這樣的內插補點的準确性就有待商榷了，而且這樣的方法看起來更像是在做“memorizing”，而不是“learning”。Yoshua Bengio 把這種稱作是 local representation，這類基于 local smoothness 假設的模型嚴重地（通常指數增長地）依賴于資料的次元（或者資料流形的本征次元），進而造成次元災難。在 ​​(Bengio, Delalleau, & Roux, 2005)​​ 一文中他還進一步指出這類方法同樣不适合學習在局部有很多變化的函數（例如像高頻的 sin 函數之類的）。實際應用中的那些問題對應的函數究竟是局部平滑的還是高頻變化的呢？高頻變化的函數如果是毫無規律的，那當然這個問題本身從資訊論的角度來說就是困難的，但是如果局部變化但是全局卻展現出規律性的話，即使局部算法無法處理，從全局出發考慮的算法也許還是可以處理的。最簡單的例子就是單純的高頻 sin 函數本身。理想情況下，如果我們有這個函數的全局模式的先驗知識的話，那麼隻要在合适的 representation 下，問題通常是可以轉化為“簡單”的形式，但是這樣的全局模式是否可以讓算法自動地通過資料學習出來呢？

而對為什麼 deep learning 會有更好的效果的一個嘗試的解釋就是 deep learning 得到的是所謂的“distributed representation” ​​(Bengio, 2009)​​, ​​(Bengio, Courville, & Vincent, 2013)​​。

核方法還有另外一個問題就是在實際使用中基本上也沒有太多的選擇，比如 ​​LIBSVM​​ 的幫助資訊裡可供選擇的核函數為：

1. -t kernel_type : set type of kernel function (default 2)
2. 0 -- linear: u'*v
3. 1 -- polynomial: (gamma*u'*v + coef0)^degree
4. 2 -- radial basis function: exp(-gamma*|u-v|^2)
5. 3 -- sigmoid: tanh(gamma*u'*v + coef0)

雖然在一些特殊的領域可能會有諸如文本核之類的 domain specific 的核函數，但是要構造一個核函數也并不是一件 trivial 的事情，因為你必須得保證它是正定的。由于這方面的限制，也有一些工作研究如何将類似于 kernel 的那一套 framework 推廣到普通的不需要正定性質的 similarity function 上 ​​(Balcan, Blum, & Srebro, 2008)​​。

另一個問題是在計算複雜性方面的：核方法的計算中牽涉到的核矩陣是  大小的，這裡  表示訓練資料點的個數，在大量資料的應用中，核矩陣不論從計算上還是存儲上都變得無比困難，雖然也有很多通過采樣子集的方法去對核矩陣進行近似的研究 ​​(Williams & Seeger, 2000)​​，但是很多時候還是不得不 fall back 到 linear kernel 上，使用另一套 formulation，可以允許計算複雜度随着資料的次元增長而不是随着資料點的個數而增長。但是這樣一來 kernel 所帶來的非線性特征映射的功能就沒有了，因為所謂 linear kernel 實際上就是等價于不使用任何 kernel 嘛。

抛開計算性能方面的考慮，就拿普通的核函數來說的話，和 deep learning 中 representation learning 還有一個重要的差別就是像高斯核之類的核函數，其對應的表達都是事先設定好的，而不是通過資料得出來的。當然，data-driven 的 kernel 方面的研究也是有不少的，比如之前有人指出 Isomap、LE 和 LLE 之類的經典的流形學習算法其實是等價于構造一個特殊的 data driven 的 kernel 然後做 kernel PCA ​​(Ham, Lee, Mika, & Scholkopf, 2004)​​，更 explicit 的 data-driven 的 Kernel 是直接将 Kernel Matrix 當做一個變量（正定矩陣）通過 Semi-Definite Programming (SDP) 來進行優化 ​​(Lanckriet, Cristianini, Bartlett, Ghaoui, & Jordan, 2004)​​，不過 SDP 雖然是凸優化，但是基本上資料規模稍微大一點就慢到不行了。

除此之外，還有一支相關的工作是 Multiple Kernel Learning (MKL)，将多個 kernel 組合起來，因為 kernel 組合時候的系數是根據 training data 優化而得的，是以這實際上也是 data-driven 的 representation learning 的一種特殊情況，并且，由于在 kernel 的基礎上在做一層組合，是以看起來已經比普通的 shallow architecture 要多一層了。Kernel 組合的系數有點類似于多層神經網絡中的 hidden layer。一般把以前最常用的隻有一層（或者沒有）hidden layer 的神經網絡（或者其他）模型叫做 shallow 的，而超過一層以上的 hidden layer 的稱為 deep 模型。

圖 3

The classical Apache “It works” page.Image from the Internet.

得到優良的 representation 是至關重要的問題，而僅僅基于 Kernel 的那種 local representation 又在 AI 相關的複雜問題前面碰到了各種瓶頸。但是為什麼一定要 deep 呢？理由有各種各樣的，但是我覺得最重要的一個理由，開源的 Web Server Apache 在若幹年來就一直在悄悄強調了：每次剛​​裝好 Apache 打開首頁面時顯示的那句​​：

It Works!

正如同一開始提到的那樣，雖然 deep model 據說很多 tricky 各種難以訓練，但是人們還是在各個應用領域裡成功地用 deep learning 的方法擊敗甚至是完敗了以前的各種 state-of-the-art。從實際應用的角度來說這已經足夠有說服力了，但是求知欲旺盛的人類當然還想知道究竟為什麼會 work。對這方面進行诠釋和探索的工作也挺多，下面列舉個别的。

圖 4

Vanship from 《Last Exile》。

其中一個解釋是從生物或者神經科學角度：因為就目前對于人類的智能系統，特别是視覺系統的研究方面表面，人腦對于這方面的資訊處理機制就是一個逐層抽象的 hierarichical architecture ​​(Serre et al., 2007)​​。雖然聽起來很有說服力，但是其實也并沒有說明為什麼多層結構更好，而隻是說人類這樣我們就跟着學了，是以這聽起來多少有點讓人想提高警惕不要被蒙混過關，Yann LeCun 在某個 tutorial 中舉過一個比較形象的例子：人類制造飛機并不是簡單地跟着動物學了在手上貼兩個翅膀就能飛的，而是在了解了為什麼那樣的結構能飛的本質原因，也就是背後的空氣動力學之類的理論之後，才真正掌握了天空飛行的“技能”。

另一方面是關于剛才讨論過的 Kernel 之類的方法無法很好地處理的所謂 Highly Variable Functions​​(Bengio, Delalleau, & Roux, 2005)​​，而 deep architecture 則可以比較有效地表達這樣的映射。更 general 地，雖然我們剛才提到隻有一層 hidden layer 的神經網絡就已經具有一定的 universal 性質，但是卻不一定是 efficient 的：存在某些函數可以簡潔地通過  層邏輯門網絡計算出來，但是如果限制為  層的話，就需要指數級别的邏輯門才行 ​​(Bengio, 2009)​​。當然還有很多問題沒有回答，比如說這些邏輯門構成的 bool 電路和機器學習問題中所遇到的函數之間的聯系是怎麼樣的 ​​(Orponen, 1994)​​？機器學習中所碰到的問題是否是這樣的 highly variable 的、必須要用 deep architecture 才能有效表達的？這樣的函數空間糾結是不是 learnable 的？在優化和求解方面有哪些困難 ​​(Glorot & Bengio, 2010)​​？是否/如何能保證學習的 generalization performance？等等等等。

實際上人們從上個世紀就各種嘗試訓練像人腦一樣的多層複雜神經網絡，但是通常在神經網絡的層數變大以後都無法訓練出理想的模型，特别是在證明隻需要一個 hidden layer 就能保證神經網絡能夠表達任意的 bool 函數 ​​(Mendelson, 2009)​​，更是變得不太有動力了。是以除了 Convolutional Network 這類結構經過專門設計的神經網絡之外，general 的 deep architecture，直到 2006 年 Hinton 他們引入 greedy layer wise pre-training ​​(Hinton, Osindero, & Teh, 2006)​​ 之後人們才第一次體會到了 deep 模型的威力。在基于 Restricted Boltzmann Machine (RBM) ​​(Hinton, Osindero, & Teh, 2006)​​ 的 pre-training 之後，又冒出了基于各種 Auto Encoder (AE) 變種 ​​(Vincent, Larochelle, Lajoie, Bengio, & Manzagol, 2010)​​, ​​(Rifai, Vincent, Muller, Glorot, & Bengio, 2011)​​ 以及甚至是 supervised 的 layer-wise pre-training ​​(Bengio, Lamblin, Popovici, & Larochelle, 2006)​​。

是以肯定會有人要問：為什麼 pre-training 會 work？是不是一定要 pre-training 才能 work？等等。一般來說，訓練神經網絡的目标函數是非常不好優化的，比如說，有非常非常多的局部最優值等等。通常認為使用 pre-training 的結果作為 back-propagation 的初始化有助于将 (stochastic) gradient descent 的初始搜尋點放在一個比較好的地方，進而收斂到比較好的（局部最優）解。另外，pre-training 還被認為是起到 regularization 的作用，能夠增強 generalization performance。關于這方面的詳細讨論，可以參考​​(Erhan, Courville, Bengio, & Vincent, 2010)​​。

至于是否一定要做 pre-training，從實驗結果方面，我們已經知道，當訓練資料足夠多的情況下，選擇好合适的（随機）初始值和神經元之間的 non-linearity 的話，不使用 pre-training 而直接進行 supervised training 也是可以得到很好的效果的 ​​(Ciresan, Meier, Gambardella, & Schmidhuber, 2010)​​, ​​(Glorot, Bordes, & Bengio, 2011)​​, ​​(Sutskever, Martens, Dahl, & Hinton, 2013)​​。不過這些結果通常都是在大量資料的情況下，結合各種 trick ​​(Montavon, Orr, & Muller, 2012)​​，再加上高性能的 GPU 裝置和特别優化的并行算法，在訓練了“足夠長”的時間之後得到的結果。是以為什麼在“大資料”時代和“GPU 并行”時代之前沒有能很成功地訓練出 deep neural network 模型似乎也并不難解釋。

而更深入的分析和 justification 方面，則通常從“deep architecture 的訓練為什麼困難”這個問題出發去探讨 ​​(Glorot & Bengio, 2010)​​。一般認為，訓練 deep neural network 的時候，目标函數本身有非常多的 local minima 和 plateaus，一階的 gradient descent 方法很容易陷入局部最優而無法自拔，是以人們自然地會想要去嘗試二階方法。不過由于神經網絡的參數非常多，Hessian 矩陣不僅計算上有困難，即使是用各種近似的方法，光是要存儲整個 Hessian 矩陣都比較麻煩。是以其中一個叫做 Hessian Free (HF) 的二階優化算法 ​​(Martens, 2010)​​ 顯得特别有意思，它利用 R-operator ​​(Pearlmutter, 1994)​​ 直接計算 Hessian 矩陣與一個向量的乘積，而不是先把 Hessian 矩陣整個算出來再用普通矩陣運算去乘以該向量。實驗結果表明使用 HF 二階優化，可以在不使用任何 pre-training 的情況下取得非常好的效果。

這裡中途插一句：有一個叫做 ​​Theano​​ 的 Python 庫，提供了 deep learning 優化相關的各種 building block，比如提供了符号運算自動推算 gradient 的功能，是以就不用自己去手算 gradient 寫 back-propagation 了，并且也內建了用于二階優化的 R-operator。最終計算用代碼會自動編譯為本地代碼以實作快速執行，并且在 GPU 裝置存在的情況下還可以無縫地編譯為 GPU 并行代碼來加速計算（雖然目前好像還隻支援 CUDA 的樣子）。有一個 ​​Deep Learning Tutorial​​ 就是使用 Theano 來介紹和實作了幾個主流的 deep learning 算法。

回到剛才的問題，HF 優化取得的成功，可以說是打開了一扇門：直接從 general 的優化算法入手，也會是一個非常值得探索的方向。不過 deep architecture 的訓練除了 local minima 和 plateaus 之外，還有一個問題就是網絡的最高兩層還非常容易 overfit，是以光看目标函數的優化有時候也并不能太說明問題：由于基本上都被最上面兩層 overfitting 去了，流回下面的層的資訊很少很少，是以下面層的 weights 幾乎沒有得到什麼 training，還停留在原始的 random initialization 階段，結果這樣的訓練結果幾乎完全沒有 generalization 能力。進來關于 rectifier non-linearity ​​(Glorot, Bordes, & Bengio, 2011)​​, ​​(Krizhevsky, Sutskever, & Hinton, 2012)​​ 相關的研究中的一個叫做 maxout ​​(Goodfellow, Warde-Farley, Mirza, Courville, & Bengio, 2013)​​ 被發現能夠使得底層的權重得到更多的 training。另外，諸如 dropout ​​(Hinton, Srivastava, Krizhevsky, Sutskever, & Salakhutdinov, 2012)​​, ​​(Wang & Manning, 2013)​​ 一類的添加 noise 也在實踐中被用作強大的 regularizer 來避免 overfitting。

雖然提到 neural network 首先想到的肯定是 overfitting，大家的着眼點也差不多都是試圖解決 overfitting 的問題，但是最近的一些實驗 ​​(Dauphin & Bengio, 2013)​​ 表明，在資料和神經網絡的規模達到一定程度之後，似乎由于優化問題的困難，導緻 under fitting 的問題也出現了。還有其他各方面的一些困難，可以參考 Yoshua Bengio 在最近的一篇文章 ​​(Bengio, 2013)​​ 中總結了一下目前在 deep learning 中碰到的各種問題和挑戰，以及可能的解決思路等等。

最後提一句關于應用方面，我倒是并沒有專門去做全面的 survey，但是目前滿天飛的 Deep Learning 相關的應用似乎大都集中在 AI 相關的經典問題（例如 Objection Recognition、Speech Recognition、NLP 之類的）方面，或者更 general 一點，很多工作集中在 classification 方面。是以說讓我覺得挺感興趣的一點是不知道這類 deep 模型是否是對于 AI 相關的問題有一些特殊的結構優勢（類比人類智能系統的層級抽象機制），或者說這類模型是否在其他非傳統 AI 領域也能取得遠超其他普通的 shallow 模型的效果呢？另外就是層級抽象或者是像 convolutional network 那樣逐層提高 invariablility 的機制對于 classification 問題來說似乎是比較自然的，但是對于 regression 呢？似乎比較少看到有用 deep neural network 去解決具體的 multi-output regression 的問題的例子的樣子。

圖 5

Neural Networks: Tricks of the Trade (2nd Edition).

至于具體的 deep learning 的模型以及相關的 training 的算法的細節之類的，原本想有時間的話也詳細整理一下，但是好像暑假即将結束，我自己也挖了好多坑都還沒有填，是以一時半會似乎不太能寫更詳細的東西了。Deep Learning 将會如何發展？究竟是否是 AI 的聖杯？就拭目以待了。​

​:)​

​

References

• Balcan, M.-F., Blum, A., & Srebro, N. (2008). A theory of learning with similarity functions. Machine Learning, 72(1-2), 89–112.
• Bengio, Y. (2009). Learning Deep Architectures for AI. Foundations and Trends in Machine Learning, 2(1), 1–127.
• Bengio, Y. (2013). Deep Learning of Representations: Looking Forward. In SLSP (pp. 1–37).
• Bengio, Y., Courville, A. C., & Vincent, P. (2013). Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell., 35(8), 1798–1828.
• Bengio, Y., Delalleau, O., & Roux, N. L. (2005). The Curse of Highly Variable Functions for Local Kernel Machines. In NIPS.
• Bengio, Y., Lamblin, P., Popovici, D., & Larochelle, H. (2006). Greedy Layer-Wise Training of Deep Networks. In NIPS (pp. 153–160).
• Ciresan, D. C., Meier, U., Gambardella, L. M., & Schmidhuber, J. (2010). Deep, Big, Simple Neural Nets for Handwritten Digit Recognition. Neural Computation, 22(12), 3207–3220.
• Dauphin, Y., & Bengio, Y. (2013). Big Neural Networks Waste Capacity. CoRR, abs/1301.3583.
• Erhan, D., Courville, A. C., Bengio, Y., & Vincent, P. (2010). Why Does Unsupervised Pre-training Help Deep Learning? AISTATS, 9, 201–208.
• Glorot, X., & Bengio, Y. (2010). Understanding the difficulty of training deep feedforward neural networks. AISTATS, 9, 249–256.
• Glorot, X., Bordes, A., & Bengio, Y. (2011). Deep Sparse Rectifier Neural Networks. AISTATS, 15, 315–323.
• Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A. C., & Bengio, Y. (2013). Maxout Networks. In ICML.
• Ham, J., Lee, D. D., Mika, S., & Scholkopf, B. (2004). A kernel view of the dimensionality reduction of manifolds. In ICML.
• Hinton, G. E., Osindero, S., & Teh, Y. W. (2006). A Fast Learning Algorithm for Deep Belief Nets.Neural Computation, 18(7), 1527–1554.
• Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. (2012). Improving neural networks by preventing co-adaptation of feature detectors. CoRR, abs/1207.0580.
• Hinton, G., Deng, L., Yu, D., Dahl, G. E., Mohamed, A., Jaitly, N., … Kingsbury, B. (2012). Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. IEEE Signal Processing Magazine, 29(6), 82–97.
• Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). ImageNet Classification with Deep Convolutional Neural Networks. In NIPS (pp. 1106–1114).
• Lanckriet, G. R. G., Cristianini, N., Bartlett, P. L., Ghaoui, L. E., & Jordan, M. I. (2004). Learning the Kernel Matrix with Semidefinite Programming. JMLR, 5, 27–72.
• Martens, J. (2010). Deep learning via Hessian-free optimization. In ICML (pp. 735–742).
• Mendelson, E. (2009). Introduction to Mathematical Logic (5th ed.). Chapman and Hall/CRC.
• Montavon, G., Orr, G., & Muller, K.-R. (2012). Neural Networks: Tricks of the Trade (2nd ed.). Springer.
• Orponen, P. (1994). Computational Complexity Of Neural Networks: A Survey. Nordic Journal of Computing.
• Pearlmutter, B. A. (1994). Fast Exact Multiplication by the Hessian. Neural Computation, 6(1), 147–160.
• Rifai, S., Vincent, P., Muller, X., Glorot, X., & Bengio, Y. (2011). Contractive Auto-Encoders: Explicit Invariance During Feature Extraction. In ICML (pp. 833–840).
• Serre, T., Kreiman, G., Kouh, M., Cadieu, C., Knoblich, U., & Poggio, T. (2007). A quantitative theory of immediate visual recognition. Progress in Brain Research, 165, 33–56.
• Sutskever, I., Martens, J., Dahl, G., & Hinton, G. (2013). On the importance of initialization and momentum in deep learning. In ICML.
• Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y., & Manzagol, P.-A. (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. JMLR, 11, 3371–3408.
• Wang, S., & Manning, C. (2013). Fast Dropout Training. In ICML.
• Williams, C. K. I., & Seeger, M. (2000). Using the Nystrom Method to Speed Up Kernel Machines. InNIPS (pp. 682–688).