題目連結:http://acm.csu.edu.cn/csuoj/problemset/problem?pid=1804
Bobo 有一個 n 個點,m 條邊的有向無環圖(即對于任意點 v,不存在從點 v 開始、點 v 結束的路徑)。
為了友善,點用 1,2,…,n 編号。 設 count(x,y) 表示點 x 到點 y 不同的路徑數量(規定 count(x,x)=0),Bobo 想知道
除以 (10 9+7) 的餘數。
其中,a i,b j 是給定的數列。
Input
輸入包含不超過 15 組資料。
每組資料的第一行包含兩個整數 n,m (1≤n,m≤10 5).
接下來 n 行的第 i 行包含兩個整數 a i,b i (0≤a i,b i≤10 9).
最後 m 行的第 i 行包含兩個整數 u i,v i,代表一條從點 u i 到 v i 的邊 (1≤u i,vi≤n)。
Output對于每組資料,輸出一個整數表示要求的值。Sample Input
3 3
1 1
1 1
1 1
1 2
1 3
2 3
2 2
1 0
0 2
1 2
1 2
2 1
500000000 0
0 500000000
1 2 Sample Output
4
4
250000014 題解:
首先,假如我們計算$\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {count\left( {i,j} \right) \times a_i \times b_j } \right)} } $
這個的時候,固定一個點i,枚舉j進行計算的話,就有:
$a_i \times \left[ {\sum\limits_{j = 1}^n {\left( {count\left( {i,j} \right) \times b_j } \right)} } \right]$
我們不妨設$dp\left[ i \right] = \sum\limits_{j = 1}^n {\left( {count\left( {i,j} \right) \times b_j } \right)} $
那麼,最後的${\rm{ans}} = \sum\limits_{i = 1}^n {\left\{ {a_i \times \left[ {\sum\limits_{j = 1}^n {\left( {count\left( {i,j} \right) \times b_j } \right)} } \right]} \right\}} $
問題來了,狀态轉移方程是什麼?
假設對于點i,它有K個子節點,就有:
$dp\left[ i \right] = \sum\limits_{k = 1}^K {\left( {b_k + dp\left[ k \right]} \right)} $
(根據題意無環圖,則存在 Edge(i→k) 就一定不存在一條路徑從k點到i點,是以計算dp[k]時就一定不會涉及到dp[i])
另外,本題如果不是有向無環圖而是一棵樹的話,很顯然,直接從樹根往下dfs計算每個節點i的dp[i]即可,
但是現在有向無環圖,可能出現如下情況:
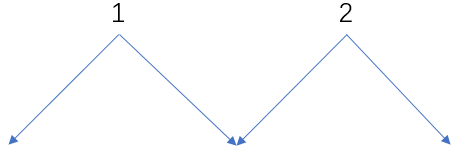
這樣一來,如果主函數裡單單dfs(1)或者單單dfs(2)都不能把整個圖上所有節點的dp[i]都計算到,
是以要把所有in-degree[i]==0的節點i都dfs(i).
AC代碼:
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
typedef long long LL;
const LL MOD=1e9+7;
const int maxn=1e5+10;
int n,m;
int indegree[maxn];
LL a[maxn],b[maxn];
LL dp[maxn];
struct Edge{
int u,v;
Edge(int u,int v){this->u=u,this->v=v;}
};
vector<Edge> E;
vector<int> G[maxn];
void init(int l,int r)
{
E.clear();
for(int i=l;i<=r;i++) G[i].clear();
}
void addedge(int u,int v)
{
E.push_back(Edge(u,v));
G[u].push_back(E.size()-1);
}
LL dfs(int u)
{
if(dp[u]!=-1) return dp[u];
dp[u]=0;
for(int i=0,_size=G[u].size();i<_size;i++)
{
Edge &e=E[G[u][i]]; int v=e.v;
dp[u]=(dp[u]+b[v]+dfs(v))%MOD;
}
return dp[u];
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF)
{
for(int i=1;i<=n;i++) scanf("%d%d",&a[i],&b[i]);
init(1,n); //鄰接表初始化
memset(indegree,0,sizeof(indegree));
for(int i=1,u,v;i<=m;i++)
{
scanf("%d%d",&u,&v);
addedge(u,v);
indegree[v]++;
}
memset(dp,-1,sizeof(dp));
for(int i=1;i<=n;i++)
{
if(indegree[i]==0) dfs(i);
}
LL ans=0;
for(int i=1;i<=n;i++) ans = ( ans + (dp[i]*a[i]) % MOD ) % MOD;
printf("%lld\n",ans);
}
}