一、深層神經網絡
深層神經網絡的符号與淺層的不同,記錄如下:
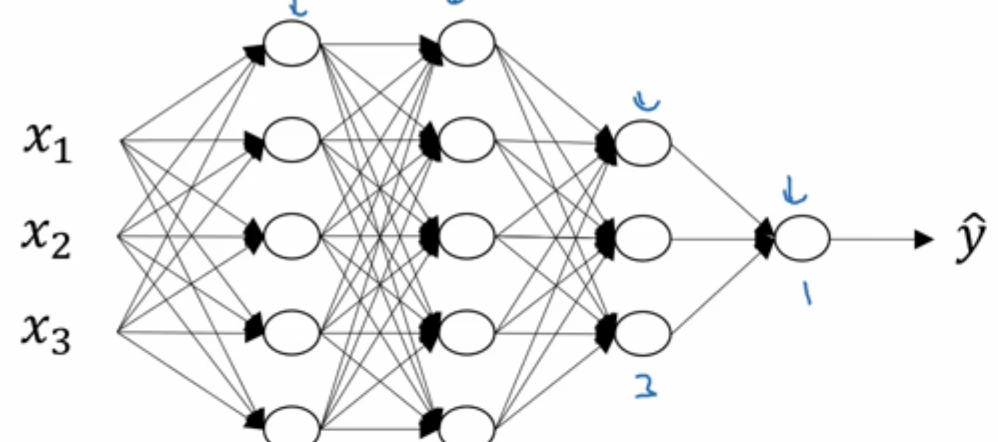
- 用\(L\)表示層數,該神經網絡\(L=4\)
- \(n^{[l]}\)表示第\(l\)層的神經元的數量,例如\(n^{[1]}=n^{[2]}=5,n^{[3]}=3,n^{[4]}=1\)
- \(a^{[l]}\)表示第\(l\)層中的激活函數,\(a^{[l]}=g^{[l]}(z^{[l]})\)
二、前向和反向傳播
1. 第\(l\)層的前向傳播
輸入為 \(a^{[l-1]}\)
輸出為 \(a^{[l]}\), cache(\(z^{[l]}\))
矢量化表示:
\[Z^{[l]}=W^{[l]}·A^{[l-1]}+b^{[l]}
\]
\[A^{[l]}=g^{[l]}(Z^{[l]})
2. 第\(l\)層的反向傳播
輸入為 \(da^{[l]}\)
輸出為 \(da^{[l-1]},dW^{[l]},db^{[l]}\)
計算細節:
\[dz^{[l]}=da^{[l]}*g^{[l]'}(z^{[l]})
\[dw^{[l]}=dz^{[l]}*a^{[l-1]}
\[db^{[l]}=dz^{[l]}
\[da^{[l-1]}=w^{[l]^T}·dz^{[l]}
\[dz^{[l]}=w^{[l+1]^T}dz^{[l+1]}*g^{[l]'}(z^{[l]})
\[dZ^{[l]}=dA^{[l]}*g^{[l]'}(z^{[l]})
\[dw^{[l]}=\frac{1}{m}dz^{[l]}·A^{[l-1]^T}
\[db^{[l]}=\frac{1}{m}np.sum(dz^{[l]},axis=1,keepdim=True)
\[dA^{[l-1]}=w^{[l]^T}·dz^{[l]}
3. 總結
前向傳播示例
反向傳播
更清晰的表示:
三、深層網絡中的前向傳播
四、核對矩陣的維數
這節的内容主要是告訴我們如何知道自己在設計神經網絡模型的時候各個參數的次元是否正确的方法。其實我自己在寫代碼的時候都得這樣做才能有信心繼續往下敲鍵盤,2333。

還是以這個神經網絡為例,各層神經網絡節點數為\(n^{[0]}=3,n^{[1]}=n^{[2]}=5,n^{[3]}=3,n^{[4]}=1\)。
先确定\(W^{[1]}\)的次元:
已知\(Z^{[1]}=W^{[1]}·X+b^{[1]}\),很容易知道\(Z^{[1]}∈R^{5×1},X∈R^{3×1}\),\(b^{[1]}\)其實不用計算就知道其次元與\(Z\)是相同的,即\(b^{[1]}∈R^{5×1}\)。根據矩陣内積計算公式可以确定\(W^{[1]}∈R^{5×3}\)。
其他層同理,不再贅述。
五、為什麼使用深層表示
為什麼要使用深層表示?
下面就從直覺上來了解深層神經網絡。
如上圖所示是一個人臉識别的過程,具體的實作步驟如下:
- 1.通過深層神經網絡首先會選取一些邊緣資訊,例如臉形,眼框,總之是一些邊框之類的資訊(我自己的了解是之是以先找出邊緣資訊是為了将要觀察的事物與周圍環境分割開來),這也就是第一層的作用。
- 2.找到邊緣資訊後,開始放大,将資訊聚合在一起。例如找到眼睛輪廓資訊後,通過往上一層彙聚進而得到眼睛的資訊;同理通過彙聚臉的輪廓資訊得到臉頰資訊等等
- 3.在第二步的基礎上将各個局部資訊(眼睛、眉毛……)彙聚成一張人臉,最終達到人臉識别的效果。
六、搭建深層神經網絡塊
上圖表示單個神經元的前向和反向傳播算法過程。
-
前向
輸入\(a^{[l-1]}\),經過計算\(g^{[l]}(w^{[l]}·a^{[l-1]}+b^{[l]})\)得到\(a^{[l]}\)
-
反向
計算\(da^{[l]}\),然後反向作為輸入,經過一系列微分運算得到\(dw^{[l]},db^{[l]}\)(用來更新權重和偏差),以及上一層的\(da^{[l-1]}\)。
推廣到整個深層神經網絡就如下圖所示:
祭上神圖:
七、參數 vs 超參數
-
參數
常見的參數即為\(W^{[1]},b^{[1]},W^{[2]},b^{[2]}……\)
- 超參數
- learning_rate: \(α\)
- iterations(疊代次數)
- hidden layer (隐藏層數量\(L\))
- hidden units (隐藏層神經元數量\(n^{[l]}\))
- 激活函數的選擇
- minibatch size
- 幾種正則化的方法
- momentum(動力、動量)後面會提到
八、這和大腦有什麼關系
主要就是說神經網絡和人的大腦運作機理貌似很相似,blabla。。。
微信公衆号:AutoML機器學習 MARSGGBO ♥原創
如有意合作或學術讨論歡迎私戳聯系~
2017-9-2