跟博弈的必敗必勝一樣的分析,後手存在必敗則先手必勝,先手全為必勝則先手必敗。
DFS時對後手的傳回值做上述兩種判斷就行。
LC 913. 貓和老鼠
方法一:必勝态分析+DFS
思路:每次走一步,鼠走的時候,如果之後存在鼠必勝(即貓必敗),則目前鼠必勝(相當于沿着必勝的方式一直走);如果之後都是貓必勝,則目前鼠必敗;如果不是這兩種情況,說明是平局。
DFS遞歸的出口:(鼠,貓,步數),關鍵:走2n步沒結果說明是平局
class Solution {
public:
int dp[55][55][105];
// (鼠,貓,步數)
int dfs(vector<vector<int>>& graph,int i, int j, int k) {
// cout << i << " " << j << " " << k << endl;
int& ret = dp[i][j][k];
if(ret != -1) return ret;
if(i == j) return ret = 2;
if(i == 0) return ret = 1;
if(k > 2*graph.size()) return ret = 0;
bool all_one = true, all_two = true;
if(k%2 == 0) { // 鼠走
for(int u : graph[i]) {
int tmp = dfs(graph, u, j, k+1);
if(tmp == 1) return ret=1;
if(tmp == 0) all_two = false;
}
if(all_two) return ret = 2;
return ret = 0;
} else { // 貓走
for(int v : graph[j]) {
if(v == 0) continue;
int tmp = dfs(graph, i, v, k+1);
if(tmp == 2) return ret=2;
if(tmp == 0) all_one = false;
}
if(all_one) return ret = 1;
return ret = 0;
}
}
int catMouseGame(vector<vector<int>>& graph) {
int n = graph.size();
memset(dp, -1, sizeof(dp));
return dfs(graph, 1, 2, 0);
}
};
方法二:極大極小博弈+DFS
最單純的極大極小算法
局面估價函數:我們給每個局面(state)規定一個估價函數值 f,評價它對于己方的有利程度。勝利的局面的估價函數值為 +oo,而失敗的局面的估價函數值為–oo。
- Max 局面:假設這個局面輪到己方走,有多種決策可以選擇,其中每種決策都導緻一種子局面(sub-state)。由于決策權在我們手中,當然是選擇估價函數值 f 最大的子局面,是以該局面的估價函數值等于子局面 f 值的最大值,把這樣的局面稱為 max 局面。
- Min 局面:假設這個局面輪到對方走,它也有多種決策可以選擇,其中每種決策都導緻一種子局面(sub-state)。但由于決策權在對方手中,在最壞的情況下,對方當然是選擇估價函數值 f 最小的子局面,是以該局面的估價函數值等于子局面 f 值的最小值,把這樣的局面稱為 max 局面。
- 終結局面:勝負已分(假設沒有和局)
大概是這樣的博弈樹,一層取最小,一層取最大。
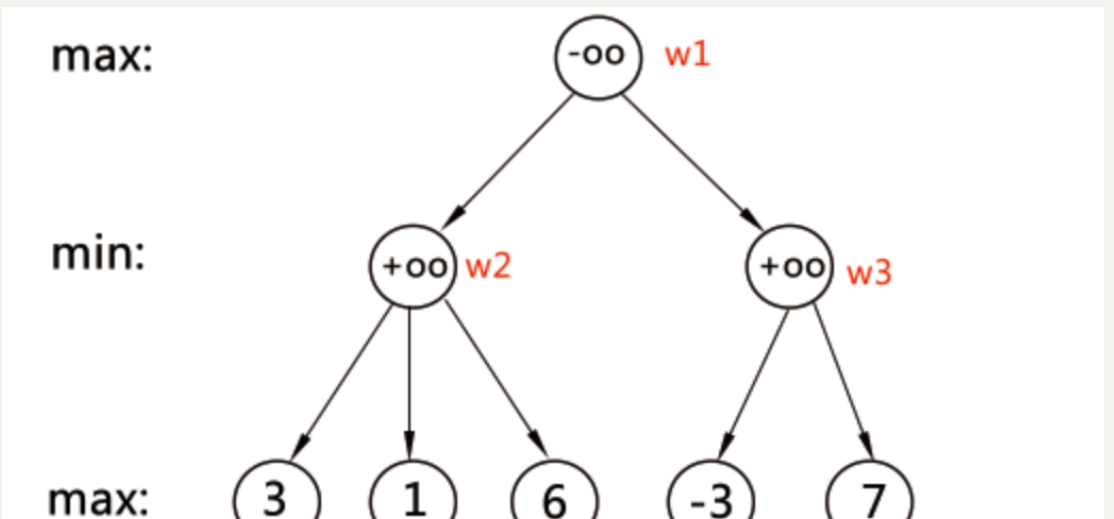
我們假設老鼠赢為 11 分,貓赢為 33 分,和局為 22 分,題目就可以轉化為最大最小博弈。對于老鼠來說,得分要盡可能小,而對于貓來說,得分要盡可能高。【參考題解喜帖-極大極小搜尋】
class Solution {
public:
int dp[55][55][105];
// (鼠,貓,步數)
// 鼠1 貓3 平局2
int dfs(vector<vector<int>>& graph,int i, int j, int k) {
// cout << i << " " << j << " " << k << endl;
int& ret = dp[i][j][k];
if(ret != -1) return ret;
if(i == j) return ret = 3;
if(i == 0) return ret = 1;
if(k > 2*graph.size()) return ret = 2;
if(k%2 == 0) { // 鼠走
ret = INT_MAX;
for(int u : graph[i]) {
ret = min(ret, dfs(graph, u, j, k+1));
if(ret == 1) return ret; // 必勝,可以不管後面的了,優化
}
return ret;
} else { // 貓走
ret = -INT_MAX;
for(int v : graph[j]) {
if(v == 0) continue;
ret = max(ret, dfs(graph, i, v, k+1));
if(ret == 3) return 3; // 優化
}
return ret;
}
}
int catMouseGame(vector<vector<int>>& graph) {
int n = graph.size();
memset(dp, -1, sizeof(dp));
int res = dfs(graph, 1, 2, 0);
if(res == 1) return 1;
else if(res == 2) return 0;
return 2;
}
};
1406. 石子遊戲 III
方法一:極大極小+DFS
方法:同樣也可以看成一個極大極小博弈問題,将後手的轉成負數,先手越大越好,後手越小越好。【參考 題解Netcan-極小化極大算法】
dfs的含義是對turn=0傳回最大值,對turn=1傳回最小值
class Solution {
public:
int dp[50005][2];
const int INF = 0x3f3f3f3f;
// 拿到了第i堆,輪到了turn
int dfs(vector<int>& stoneValue, int i, int turn) {
int n = stoneValue.size();
if(i >= n) return 0;
int& ret = dp[i][turn];
if(ret != INF) return ret;
int cur = 0;
if(turn == 0) { // turn=0, Alice拿
ret = -INF;
for(int k = 0;k < 3 && i+k< n;k++) {
cur += stoneValue[i+k];
ret = max(ret, cur + dfs(stoneValue, i+k+1, !turn));
}
} else {
ret = INF;
for(int k = 0;k < 3 && i+k< n;k++) {
cur -= stoneValue[i+k];
ret = min(ret, cur + dfs(stoneValue, i+k+1, !turn));
}
}
return ret;
}
string stoneGameIII(vector<int>& stoneValue) {
memset(dp, INF, sizeof(dp)); // -0x3f3f3f3f不能這樣填充
int res = dfs(stoneValue, 0, 0);
cout << "res: " << res << endl;
if(res > 0) return "Alice";
if(res < 0) return "Bob";
return "Tie";
}
};
方法二:極大極小簡化版
由于turn每次都是反轉過來,上面的代碼進一步簡化(記憶化不能丢,不讓會逾時)
目前值減去後手的-每種情況最大值,這裡DFS的含義就是(i, turn)的最大值
class Solution {
public:
int dp[50005][2];
const int INF = 0x3f3f3f3f;
// 拿到了第i堆,輪到了turn
int dfs(vector<int>& stoneValue, int i, int turn) {
int n = stoneValue.size();
if(i >= n) return 0;
int& ret = dp[i][turn];
if(ret != INF) return ret;
int cur = 0;
ret = -INF;
for(int k = 0;k < 3 && i+k< n;k++) {
cur += stoneValue[i+k];
ret = max(ret, cur - dfs(stoneValue, i+k+1, !turn));
}
return ret;
}
string stoneGameIII(vector<int>& stoneValue) {
memset(dp, INF, sizeof(dp)); // -0x3f3f3f3f不能這樣填充
int res = dfs(stoneValue, 0, 0);
cout << "res: " << res << endl;
if(res > 0) return "Alice";
if(res < 0) return "Bob";
return "Tie";
}
};
方法三:線性遞推,改成DP
很容易發現,上面的狀态可以倒推得到,而且是線性遞推(不像貓捉老鼠是圖結構),是以可以改成dp。
class Solution {
public:
string stoneGameIII(vector<int>& stoneValue) {
int n = stoneValue.size();
vector<vector<int>>dp(n+1, vector<int>(2, INT_MIN));
dp[n][0] = dp[n][1] = 0;
for(int i = n-1;i>=0;i--) {
for(int turn = 0;turn < 2;turn++) {
int sum = 0;
for(int k = 0;k < 3 && i+k < n;k++) {
sum += stoneValue[i+k];
dp[i][turn] = max(dp[i][turn], sum - dp[i+k+1][!turn]);
}
}
}
int res = dp[0][0];
// cout << "res: " << res << endl;
if(res > 0) return "Alice";
if(res < 0) return "Bob";
return "Tie";
}
};
LC 1510. 石子遊戲 IV
方法:博弈最簡單的例題了,線性的,沒有平局。這裡采用必勝必敗分析,也可以用極大極小(必勝必敗算是其特例),也可以遞推。
class Solution {
public:
int dp[100005];
int dfs(int n) {
// cout << "n: " << n << endl;
if(n == 0) return 0;
int& ret = dp[n];
if(ret != -1) return ret;
int gen = sqrt(n);
for(int i = 1;i <= gen;i++) {
if(dfs(n-i*i) == 0) return ret=1; // 後手存在必敗,則先手必勝
}
return ret=0; // 由于沒有平局,一定為必敗
}
bool winnerSquareGame(int n) {
memset(dp, -1, sizeof(dp));
return dfs(n);
}
};
個性簽名:時間會解決一切