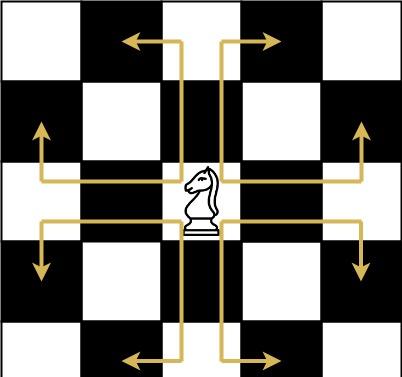
The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
n
n
we can dial.
You are allowed to place the knight on any numeric cell initially and then you should perform
n - 1
n
. All jumps should be valid knight jumps.
As the answer may be very large, return the answer modulo
109 + 7
.
Example 1:
Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
Example 2:
Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]
Example 3:
Input: n = 3
Output: 46
Example 4:
Input: n = 4
Output: 104
Example 5:
Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod.
Constraints:
-
1 <= n <= 5000
這道題說是有一種騎士撥号器,在一個電話撥号盤上跳躍,其跳躍方式是跟國際象棋中的一樣,不會國際象棋的童鞋可以将其當作中國象棋中的馬,馬走日象飛田。這個騎士可以放在 10 個數字鍵上的任意一個,但其跳到的下一個位置卻要符合其在國際象棋中的規則,也就是走日。現在給了一個整數N,說是該騎士可以跳N次,問能撥出多個不同的号碼,并且提示了結果要對一個超大數字取餘。看到這裡,對于各位刷題老司機來說,肯定能反應過來要用動态規劃 Dynamic Programming 了吧,因為數字可能巨大無比,強行暴力遞歸破解可能會爆棧。這裡使用一個二維數組 dp,其中 dp[i][j] 表示騎士第i次跳到數字j時組成的不同号碼的個數,那麼最終所求的就是将 dp[N-1][j] 累加起來,j的範圍是0到9。接下來看狀态轉移方程怎麼寫,當騎士在第i次跳到數字j時,考慮其第 i-1 次是在哪個位置,可能有多種情況,先來分析撥号鍵盤的結構,找出從每個數字能到達的下一個位置,可得如下關系:
0 -> 4, 6
1 -> 6, 8
2 -> 7, 9
3 -> 4, 8
4 -> 3, 9, 0
5 ->
6 -> 1, 7, 0
7 -> 2, 6
8 -> 1, 3
9 -> 4, 2
可以發現,除了數字5之外,每個數字都可以跳到其他位置,其中4和6可以跳到三個不同位置,其他都隻能取兩個位置。反過來想,可以去的位置,就表示也可能從該位置回來,是以根據目前的位置j,就可以在數組中找到上一次騎士所在的位置,并将其的 dp 值累加上即可,這就是狀态轉移的方法,由于第一步是把騎士放到任意一個數字上,就要初始化 dp[0][j] 為1,然後進行狀态轉移就行了,記得每次累加之後要對超大數取餘,最後将 dp[N-1][j] 累加起來的時候,也要對超大數取餘,參見代碼如下:
解法一:
class Solution {
public:
int knightDialer(int N) {
int res = 0, M = 1e9 + 7;
vector<vector<int>> dp(N, vector<int>(10));
vector<vector<int>> path{{4, 6}, {6, 8}, {7, 9}, {4, 8}, {3, 9, 0}, {}, {1, 7, 0}, {2, 6}, {1, 9}, {4, 2}};
for (int i = 0; i < 10; ++i) dp[0][i] = 1;
for (int i = 1; i < N; ++i) {
for (int j = 0; j <= 9; ++j) {
for (int idx : path[j]) {
dp[i][j] = (dp[i][j] + dp[i - 1][idx]) % M;
}
}
}
for (int i = 0; i < 10; ++i) res = (res + dp.back()[i]) % M;
return res;
}
};
我們也可以用遞歸+記憶數組的方式來寫,整體思路和疊代的方法并沒有什麼差別,之前類似的題目也不少,就不多解釋了,可以對照上面的講解和代碼來了解,參見代碼如下:
解法二:
class Solution {
public:
int knightDialer(int N) {
int res = 0, M = 1e9 + 7;
vector<vector<int>> memo(N + 1, vector<int>(10));
vector<vector<int>> path{{4, 6}, {6, 8}, {7, 9}, {4, 8}, {3, 9, 0}, {}, {1, 7, 0}, {2, 6}, {1, 9}, {4, 2}};
for (int i = 0; i < 10; ++i) {
res = (res + helper(N - 1, i, path, memo)) % M;
}
return res;
}
int helper(int n, int cur, vector<vector<int>>& path, vector<vector<int>>& memo) {
if (n == 0) return 1;
if (memo[n][cur] != 0) return memo[n][cur];
int res = 0, M = 1e9 + 7;
for (int idx : path[cur]) {
res = (res + helper(n - 1, idx, path, memo)) % M;
}
return memo[n][cur] = res;
}
};
Github 同步位址:
https://github.com/grandyang/leetcode/issues/935
類似題目:
Letter Combinations of a Phone Number
參考資料:
https://leetcode.com/problems/knight-dialer/
https://leetcode.com/problems/knight-dialer/discuss/189265/Concise-Java-DP-Solution
https://leetcode.com/problems/knight-dialer/discuss/189271/Java-Top-Down-Memo-DP-O(N)
https://leetcode.com/problems/knight-dialer/discuss/190787/How-to-solve-this-problem-explained-for-noobs!!!
LeetCode All in One 題目講解彙總(持續更新中...)
喜歡請點贊,疼愛請打賞❤️~.~| 微信打賞 | Venmo 打賞 |