在前面專題中講的BST、AVL、RBT都是典型的二叉查找樹結構,其查找的時間複雜度與樹高相關,都是在記憶體中進行的。那麼降低樹高自然對查找效率是有所幫助的。
另外還有一個比較實際的問題:就是大量資料存儲中,實作查詢這樣一個實際背景下,平衡二叉樹由于樹深度過大而造成磁盤IO讀寫過于頻繁,進而導緻效率低下。那麼如何減少樹的深度(當然不能減少查詢資料量),一個基本的想法就是:
1. 每個節點存儲多個元素(但元素數量不能無限多,否則查找就退化成了節點内部的線性查找了)。
2. 摒棄二叉樹結構,采用多叉樹(由于節點内元素數量不能無限多,自然子樹的數量也就不會無限多了)。
多路查找樹(muitl-way search tree) 每個節點的孩子可以樹可以多餘兩個; 每個節點可以存儲多個元素;
1、2-3樹
每個節點都具有2個孩子(稱之為2節點)或者3個孩子(稱之為3節點)。
一個2節點包含一個元素和兩個孩子(或沒有孩子)。
一個3節點包含兩個元素和三個孩子(或沒有孩子)。
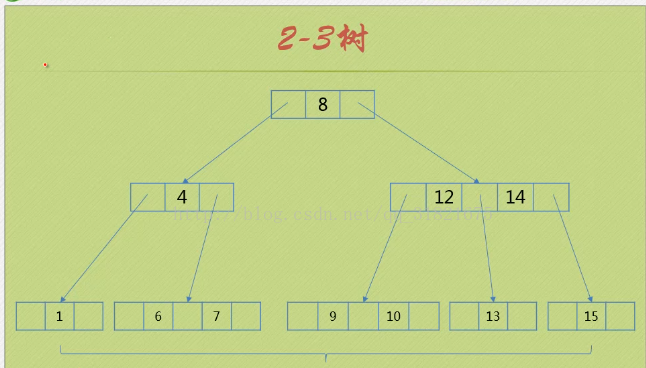
1.1. 2-3樹的插入實作
1.對于空樹 插入一個節點直接插入就好。
2.插入節點到一個2節點的葉子上。 比如插入3
3.将一個節點插入到原來上3節點的葉子上
3.1要在3節點上插入,此時3節點的上面是2節點 則将 上面的2節點變成3節點 比如插入5
3.2 要在3節點上插入,此時3節點上面是3 節點 則将上面首次出現為2節點的節點變成3節點。比如插入11
以前我們普通二叉樹 插入時都是在葉子節點後添加,這樣會導緻二叉樹的高度不斷增加。查找困難。
此時 我們用2-3樹時重複分利用特性。 往上尋找有用空間 進行有效的利用
3.3 要在3節點插入資料時 ,該3節點往上周遊都是3節點,這時要擴充高度了。
1.2 2-3樹的删除實作。
1.要删除的數位于3節點位址上。 3節點 ->2節點就好 比如删除6
2.要删除的數位于2葉子節點上。
1.此葉子節點上一級是2節點,但是他有一個3節點的有孩子。
2.此葉子節點上一級是2節點,但是他有一個2節點的有孩子。
3.此葉子節點雙親是一個3節點。
4.删除的是一個滿二叉樹葉子節點
5. 要删除的元素位于非葉子節點的分支上。
當是2節點時 則按照中序周遊 找此節點前面或者後面的數頂底下。
當是3 節點的時候 将3節點的左孩子提升上去