資料結構（六）—— 散列查找（2）：散列函數的構造方法

• 2. 散列函數的構造方法
• • 2.1 數字關鍵詞的散列函數構造
  • 2.2 字元關鍵詞的散列函數構造

  一個 “好”的散列函數一般應考慮下列兩個因素：

    1. 計算簡單，以便提高轉換速度；

    2. 關鍵詞對應的位址空間分布均勻，以盡量減少沖突。

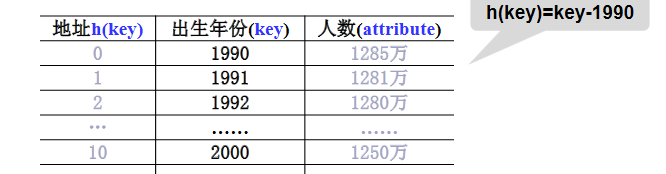
   1．直接定址法： 取關鍵詞的某個線性函數值為散列位址，即 h ( k e y ) = a × k e y + b h(key) = a \times key + b h(key)=a×key+b (a、b為常數)。

   2．除留餘數法：散列函數為：h(key) = key mod p

            例： h(key) = key % 17

   這裡：p =Tablesize = 17，一般p取素數。

   3．數字分析法 ：分析數字關鍵字在各位上的變化情況，取比較随機的位作為散列位址。

             比如： 取11位手機号碼key的後4位作為位址：

                 散列函數為： h(key) = atoi(key+7) (char *key)

                 如果關鍵詞key是18位的身份證号碼：

h 1 ( k e y ) = ( k e y [ 6 ] − ′ 0 ′ ) × 1 0 4 + ( k e y [ 10 ] − ′ 0 ′ ) × 1 0 3 +                                                                         ( k e y [ 14 ] − ′ 0 ′ ) × 1 0 2 + ( k e y [ 17 ] − ′ 0 ′ ) × 10 + ( k e y [ 17 ] − ′ 0 ′ ) h ( k e y ) = h 1 ( k e y ) × 10 + 10             ( 當 k e y [ 18 ] = ′ x ′ 時 )                                                                                 或     = h 1 ( k e y ) × 10 + k e y [ 18 ] − ′ 0 ′             ( 當 k e y [ 18 ] 為 ′ 0 ′   ′ 9 ′ 時 )                                       \begin{matrix}h_{1}(key)=(key[6]-'0') \times 10^{4}+(key[10]-'0') \times 10^{3}+\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\\ (key[14]-'0') \times 10^{2}+(key[17]-'0') \times 10+(key[17]-'0') \\ \\h(key)=h_{1}(key)\times 10+10 \ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}(當key[18]='x'時)\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\\ 或\ _ {}\ _ {}=h_{1}(key)\times 10+key[18]-'0' \ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {} (當key[18]為'0'~'9'時)\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {}\ _ {} \end{matrix} h1​(key)=(key[6]−′0′)×104+(key[10]−′0′)×103+ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​(key[14]−′0′)×102+(key[17]−′0′)×10+(key[17]−′0′)h(key)=h1​(key)×10+10 ​ ​ ​ ​ ​ ​(當key[18]=′x′時) ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​或 ​ ​=h1​(key)×10+key[18]−′0′ ​ ​ ​ ​ ​ ​(當key[18]為′0′ ′9′時) ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​​   4．折疊法 ：把關鍵詞分割成位數相同的幾個部分，然後疊加。

         如： 56793542

   5．平方取中法

      如： 56793542

   1．一個簡單的散列函數 —— ASCII碼加和法

      對字元型關鍵詞key定義散列函數如下：

      h ( k e y ) = ( ∑ k e y [ i ] ) h(key)=(\sum key [i]) h(key)=(∑key[i]) mod TableSize

      沖突嚴重：a3、b2、c1；eat、 tea；

   2．簡單的改進 —— 前3個字元移位法

      h ( k e y ) = ( k e y [ 0 ] × 2 7 2 + k e y [ 1 ] × 27 + k e y [ 2 ] ) h(key)=(key[0]\times27^{2} + key[1]×27 + key[2]) h(key)=(key[0]×272+key[1]×27+key[2]) mod TableSize

      仍然沖突：string、 street、strong、structure等等；

      空間浪費： 3000 / 2 6 3 = 30 % 3000/26^{3} = 30\% 3000/263=30%

Index Hash (const char *Key, int TableSize )
{
    unsigned int h = 0;  /*散列函數值，初始化為0*/
    while ( *Key != '\0')  /*位移映射*/
        h = ( h << 5 ) + *Key++;
    return h % TableSize;
}