淺談P/NP問題

　　克雷數學研究所(Clay Mathematics Institute，CMI)是在1998年由商人蘭頓·克雷(Landon T. Clay)和哈佛大學數學家亞瑟·傑夫(Arthur Jaffe)創立，蘭頓·克雷資助的一家非牟利私營機構，總部在麻薩諸塞州劍橋市，機構的目的在于促進和傳播數學知識。克雷數學研究所給予有潛質的數學家各種獎項和資助，該研究所在2000年5月24日公布的七個千禧年難題，它們是：

　　（1）霍奇猜想

　　（2）龐加萊猜想

　　（3）黎曼假設

　　（4）楊-米爾斯規範場存在性和品質間隔假設

　　（5）NS方程解的存在性與光滑性

　　（6）貝赫和斯維讷通-戴爾猜想

　　（7）P=NP?

　　這七個問題被研究所認為是“重要的經典問題，經許多年仍未解決”。解答任何一題的第一個人将獲頒予一百萬美元獎金，是以這七個問題共值七百萬美元。

　　近20年過去了，在這7個問題中，隻有龐加萊猜想得到了解決。對于普通的程式員來說，前6個難題或許過于遙遠，但是你一定聽說過NP問題的大名。

水浒英雄卡的故事

　　在我讀高中的時候，小浣熊幹脆面中的水浒英雄卡曾經風靡一時。當時1998年央視版的《水浒傳》剛開播不久，再加上課本上《魯提轄拳打鎮關西》和《林教頭風雪山神廟》的助攻，同學們收集英雄卡的熱情空前高漲。

　　卡片雖然精美，但是每袋幹脆面隻有一張英雄卡，想要收集齊全頗為不易。一個快速收集的辦法就是多買幹脆面。當時的高中生并沒有多少零花錢，最富裕的同學也不過每天買兩袋。在收集時也發現了另一個問題，如果在同一家店買，那麼得到重複英雄卡的幾率會大大增加，有個運氣極差的同學連吃了兩星期幹脆面，居然得到了十幾張豹子頭林沖。

　　住校的同學紛紛求助于我這種走讀生，于是我每天多了一個任務，在上學路上的每一所食雜店購買小浣熊幹脆面。

　　英雄卡的人物漸漸豐富起來，大家還互相交換，隻是到了畢業，仍然沒有人把全套英雄卡收集齊全。

　　回顧水浒英雄卡的故事，無論是加大購買量還是擴大購買範圍，都很難達成“收集全套卡片”的最終目标，整個過程費時費力又費錢，還需要很大的運氣成分。如果沒有網購平台，我甚至都不知道是否真有人能夠集全。

　　水浒英雄卡的故事就是一個P/NP問題，它的焦點在于，集全英雄卡的過程是否能夠變得輕而易舉？

這些奇怪的名字

　　計算機可以幫助我們解決很多問題，但是仍有一部分問題可能永遠無法通過簡單的計算得到答案，試着解答它們是計算機科學家和數學們的重要挑戰。人們給這類問題了一個奇怪的名字——P/NP問題。

P和NP

　　我們讨論的“有效”算法幾乎都是多項式時間算法，P/NP中的P就是指多項式時間（Polynomial）。一個複雜問題如果能在多項式時間内解決，它就被稱為P問題，這意味着計算機很容易求解。

　　NP問題就是除了P問題之外的問題嗎？如果是就好了。世界總是很複雜，有時候我們并不用能證明一個問題能在多項式時間内解決，同時也沒法證明它不能在多項式時間内解決，也就是說這個問題是懸案，在當下看起來沒法有效解決，但是誰也說不準在未來是否能很容易解決。對于這類問題，簡單地歸為非P類問題就不和合适了，就像我們無法把建立月球基地和建立銀河星系聯盟歸為非P類問題。

　　NP問題不是非P類問題，NP不是“Not P”的意思，NP指非确定性多項式時間（nondeterministic polynomial）。NP問題強調的不是“是否能在多項式時間内找到解”，而是“是否能夠在多項式時間内驗證解”，如果一個問題的解可以在多項式的時間内被驗證，那麼這個問題就是NP問題。

　　我們在 密碼疑雲 (3)——詳解RSA的加密與解密 中曾提到了RSA加密機制的原理：“将兩個大素數相乘很容易，但是想要對它們的乘積進行素因子分解卻極其困難”。假如有人告訴你3999991可以分解成兩個素數的乘積，也許你不知道可以分解成哪兩個素數，但是如果告訴你這兩個素數是1997和2003，那麼你很容易計算出1997×2003=3999991。

　　大整數的素因子分解就是典型的NP問題，有沒有多項時間的分解算法并不重要，重要的是如果有人給了你兩個素數，你很容易驗證這兩個素數的乘積是否是那個大整數。這符合一般的認知：在大多數時候，驗證一個解比得到一個解更容易。

　　既然能在多項式時間内解決一個問題，必然也能在多項式時間内驗證這個問題的解，這意味着所有的P問題都是NP問題，P∈NP。

P=NP？

　　大約在公元前4200年，古代埃及人按尼羅河水的漲落和農作物生長的規律，把一年分為泛濫季、耕種季、收獲季3個季節，每季分為4個月，每月30天，歲末增加5天節日，共計365天。

　　5000多年前，中國就有《陰陽曆》，每年366天。魏晉南北朝（公元220年～公元518年）時期，祖沖之制定《大明曆》，首次将歲差計算入内，每年365.2428天，與現在的精确測量值僅相差52秒。

　　古代瑪雅人已經知道了一些天體的精确運作周期，他們測得太陽年的長度是365.2420天，比現代的測量值365.2422隻至少了0.0002天，相當于17.28秒。

　　經過漫長的歲月，不同的文明在不同的時期分别獨立發現了地球公轉的規律，進而制定了曆法，這至少從哲學上證明“曆法”這一概念是真實存在的。類似地，在不同時期的人們對很多不同領域問題的研究中，也都不約而同地提出了相同的問題——是否所有的NP問題都是P問題？也就是說，是否所有能夠在多項式時間内驗證的問題都可以在多項式時間内解決？這個問題被簡稱為“P=NP？”

　　所謂的“P/NP問題”，其實就一句話：證明或推翻P=NP。隻要證明一個任意規模下的NP問題都可以在多項式時間内求解，就可以說對于該問題P=NP，即該問題是一個P問題。

NPC問題

　　我經常聽到程式員們在讨論問題時說：“××是NP問題，隻能用蠻力法。” 程式員們的說法并不完全準确，NP問題可沒有強調非得用蠻力法，隻強調了在有解的情況下可以輕松地驗證解，他們真正指的應該是NPC問題。

　　NPC問題也稱NP完全問題，是NP-Complete的縮寫。NPC問題滿足兩點，首先，NPC問題肯定也是NP問題；其次，所有NP問題都能夠在多項式時間内規規約到NPC問題。為什麼要将NP問題規約到NPC問題呢？這是因為人們發現某些NP問題的複雜性與整個類的複雜性相關聯，如果這些問題中的任何一個存在多項式時間的算法，那麼所有該類問題都是多項式時間可解的。這也符合常理，NPC問題是NP問題規約來的，是以NPC問題的難度一定大于NP問題，隻要能在多項式時間内解決NPC問題，那麼NP問題也能在多項式時間内解決，此時NP問題也就變成了P問題，P=NP。

　　在《西遊記》的第二回中，孫悟空學成本領回到花果山後，得知很多猴子猴孫被混世魔王擄走，連水簾洞中的石盆、石碗也被搶了去。大怒的孫悟空在混世魔王的老巢将其“照頂門一下，砍為兩段。領衆殺進洞中，将那大小妖精，盡皆剿滅。”在解救了衆猴後，對衆道：

　　“汝等跟我回去。”衆猴道：“大王，我們來時，隻聽得耳邊風聲，虛飄飄到于此地，更不識路徑，今怎得回鄉？”悟空道：“這是他弄的個術法兒，有何難也！我如今一竅通，百竅通，我也會弄。你們都合了眼，休怕！”

　　花果山的小猴們顯然沒法在多項式時間内“弄的個術法兒”，但是能很容易驗證“弄的個術法兒”的結果，就是“隻聽得耳邊風聲，虛飄飄到于此地”，是以可以把混世魔王的法術看作NP問題。至于孫悟空，在學藝時從沒把猴子或類似的動物攝到空中，隻修習了筋鬥雲和七十二變，但由于七十二變是高端的NPC法術，是以“一竅通，百竅通”，不僅能順利地把衆猴帶回花果山，還在後續的大鬧天宮和西天取經路上施展過諸如三頭六臂、身外身、隐身法、定身術、元神出竅、法天象地、擔山趕月等其他NP法術。

　　NPC問題是在P問題與NP問題上的一個重大進展，問題是，想要在NPC問題上找到一個多項式時間内的算法出奇地困難，難倒人們甚至不相信存在這樣的算法，就像孫悟空的“一竅通，百竅通”一樣，反正我沒見過誰能做到。

　　另一個具有代表性的NPC問題是銷售員旅行問題(traveling salesman problem)。一個推銷員要從北京出發，經過上海、南京、杭州、南昌、廣州等n個城市，最後傳回北京。每兩個城市之間都有直達的飛機、高鐵等交通工具。銷售員的交通費用預算是Q，他在每個城市僅駐留一次，是否存在這樣一個行程，銷售員既能周遊所有城市，又能讓總費用小于Q？

　　有人說這還不簡單？從北向南走就好了。現實生活中也許我也會這麼安排，但是加上預算費用後就不是那麼回事了。雖然上海到南京很近，但也許正好有一趟上海到廣州的特價航班，這時候又該怎麼選擇呢？如果用蠻力法周遊，3個城市間會産生2！種路線，10個城市會産生9！=362880種路線，20個城市會産生19！≈1.21×1017種路線，在這麼多種路線中挑選，簡直太可怕了。

　　銷售員旅行問題可以規約為圖論中一個著名的問題，已給一個n個點的完全圖（圖中每兩個頂點之間都存在權值已知的邊），求每個頂點正好周遊一次，且總權值小于某個值的封閉回路。這是一個NPC問題，迄今為止仍未一個找到一個能夠應對大型問題的有效算法。正是由于NPC問題的存在，才使人們普遍相信P≠NP。

NP-hard

　　NP-hard問題也稱NP難題，從名字就知道，它是NP家族中最難的。NPC問題屬于NP-hard問題，是以NP-hard問題肯定沒有能在多項式時間内找到解算法，至少目前沒有。NP-hard問題之是以hard，是因為對于一些NP-hard問題來說，即使給出解，也難以在多項式時間内驗證，是以NP-hard問題未必是NP問題。

　　“難以在多項式時間内找到解”容易了解，“即使給出解，也難以在多項式時間内驗證”又是怎麼回事呢？我們把銷售員旅行的問題稍作修改，求使銷售員能周遊所有城市，每個城市僅駐留一次，且總費用最小的行程。首先可以确定至少目前為止還不存在有效的算法，現在給了你一個解并告訴你這就是最終解，你如何确定它的正确性呢？辦法大概還是周遊，把這個解與所有其它行程比對，進而确定它是否是最優的，驗證解的複雜度仍然是n!。

　　NP、NPC、NP-hard的關系：

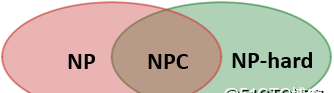
如何面對NP問題

　　從廣義來說，在承認P≠NP的前提下，NP問題也指難以在多項式時間内求解的問題（本章所指的NP問題都廣義的NP問題）。在實際工作中，我們經常會遇到很難解決的問題，如果這些問題是NP問題，又該怎麼辦呢？

琪琳的甜品創新程式

　　琪琳是“甜品之家”的程式員，她為公司編寫了一個甜品創新的程式，這個程式能夠微調各種配料，找到最具口感的甜品。公司使用這個程式開發了一系列爆款的産品，大賺了一筆。經理最近突發奇想，打算制作一款“風味獨特”的小甜餅，這款小甜餅不僅能夠滿足所有人的味蕾，甚者能讓一個獨眼蛤蟆開心地笑起來。但是這次，被寄予厚望的程式失靈了，這可難壞了琪琳，連續加班一個月都沒有絲毫進展。另一公室的劉闖得知了情況，拍拍琪琳的肩膀說：“這很明顯是個NP問題，科學家都不相信有辦法解決。别浪費腦細胞了，咱們一起去打乒乓球吧！” 琪琳恍然大悟，真的去打乒乓球了。沒過多久，經理就以“工作不負責任”為由，扣掉了她的項目獎金。

7個應對辦法

　　對于NP完全問題，雖然我們确信無法找到一個快速的解決方案，但生活仍要繼續，問題還是要解決，此時不妨試試下面的7個辦法。

　　1. 縮小問題規模

　　NP完全問題之是以困難，最重要的原因之一就是搜尋規模過于龐大，是以适當地縮小問題規模就成了需要首先思考的問題。

　　在建構機器學習模型時，經常面對過于複雜的資料特征，這就需要用到資料降維技術。 資料降維，是解決資料“維數災難”的有效手段，即通過某種數學變換将原始高維屬性空間轉變為一個低維的“子空間”，進而極大地縮小的原始問題的規模。

　　實際上“降維”并不僅僅存在于機器學習和科幻小說中，它就在我們身邊。《三國演義》為我們鋪開了近100年的曆史畫卷，這裡既有軍閥割據的混戰，又有政治和軍事的争鬥，更有叱詫風雲的英雄人物。神奇的是，這些多元度的故事通過“文字”這一工具實作了有效的降維，進而有效縮小了問題的規模，最終呈現在平面媒體上。

　　除了降維外，設定限制條件也是縮小問題規模的有效手段。

　　在《三體2·黑暗森林》中，作為“面壁者”邏輯向大史提出了一個NP問題——找一個二十歲左右的夢中女孩兒：

羅輯啜了一口酒，坐到史強身邊：“大史啊，我求你幫個忙。在你以前的工作中，是不是常常在全國甚至全世界範圍找某個人？”“是。我對此很在行，找人嗎？”“當然。那好，幫我找一個人，一個二十歲左右的女孩兒，這是計劃的一部分。國籍、姓名、住址？都沒有，她甚至連在這個世界上存在的可能性都很小。”大史看着羅輯，停了幾秒鐘說：“夢見的？”羅輯點點頭：“包括白日夢。”

　　這個“二十歲左右的女孩兒”是邏輯夢中的完美女友，人海茫茫，能否找到隻能看緣分，甚至是否存在都說不準，估計絕大多數人都會拒絕或敷衍這個找人的請求。但是閱人無數的大史警官并沒有回絕，而是嘗試讓客戶捋清需求，問清這個女孩的具體長相、愛好和其他屬性：

　　“她是一個，嗯，東方女孩，就設定為中國人吧。”羅輯說着，拿出紙和筆畫了起來，“她的臉型，是這個樣子；鼻子，這樣兒，嘴，這樣兒，唉，我不會畫，眼睛……見鬼，我怎麼可能畫出她的眼睛？你們是不是有那種東西，一種軟體吧，可以調出一張面孔來，按照目擊者描述調整眼睛鼻子什麼的，最後精确畫出目擊者見過的那人？”

　　“有啊，我帶的筆記本裡就有。”

　　“那你去拿來，我們現在就畫！”

　　大史在沙發上舒展一下身體，讓自己坐得舒服些，“沒必要，你也不用畫了，繼續說吧，長相放一邊，先說她是個什麼樣的人。”

　　羅輯體内的什麼東西好像被點燃了，他站起來，在壁爐前躁動不安地來回走着，“她……怎麼說呢？她來到這個世界上，就像垃圾堆裡長出了一朵百合花，那麼……那麼的純潔嬌嫩，周圍的一切都不可能污染她，但都是對她的傷害，是的，周圍的一切都能傷害到她！你見到她的第一反應就是去保護她……啊不，呵護她，讓她免受這粗陋野蠻的現實的傷害，你願意為此付出一切代價！她……她是那麼……唉，你看我怎麼笨嘴笨舌的，什麼都沒說清。”

　　“都這樣。”大史笑着點點頭，他那初看有些粗傻的笑現在在羅輯的眼中充滿智慧，也讓他感到很舒服，“不過你說得夠清楚了。”

　　“好吧，那我接着說，她……可，可我怎麼說呢？怎樣描述都說不出我心中的那個她。”羅輯顯得急躁起來，仿佛要把自己的心撕開讓大史看似的。

　　邏輯提供了一大堆無助解決問題的資訊，僅僅是在需求外圍打轉，這種場景是否似曾相識？于是大史開始引導邏輯：

　　大史揮揮手讓羅輯平靜下來，“算了，就說你和她在一起的事兒吧，越詳細越好。”

　　羅輯吃驚地瞪大了雙眼，“和她……在一起？你怎麼知道？”

　　大史又呵呵地笑了起來，同時四下看了看，“這種地方，不會沒有好些的雪茄吧？”

　　“有有！”羅輯趕忙從壁爐上方拿下一個精緻的木盒，從中取出一根粗大的“大衛杜夫”，用一個更精緻的斷頭台外形的雪茄剪切開頭部，遞給大史，然後用點雪茄專用的松木條給他點着。

　　大史抽了一口，惬意地點點頭，“說吧。”

　　羅輯一反剛才的語言障礙，滔滔不絕起來。他講述了她在圖書館中的第一次活現，講述他與她在宿舍裡那想象中的壁爐前的相逢，講她在他課堂上的現身，描述那天晚上壁爐的火光透過那瓶像晚霞的眼睛的葡萄酒在她臉龐上映出的美麗。他幸福地回憶他們的那次旅行，詳細地描述每一個最微小的細節：那雪後的田野、藍天下的小鎮和村莊、像曬太陽的老人的山，還有山上的黃昏和篝火……

　　在收集到一些資訊後，大史開始縮小問題規模，将複雜的描述拆解成一個個定類屬性：

　　大史聽完，撚滅了煙頭說：“嗯，基本上夠了。關于這個女孩兒，我提一些推測，你看對不對。”

　　“好的好的！”

　　“她的教育程度，應該是大學以上博士以下。”

　　羅輯點頭，“是的是的，她有知識，但那些知識還沒有達到學問的程度去僵化她，隻是令她對世界和生活更敏感。”

　　“她應該出生在一個進階知識分子家庭，過的不是富豪的生活，但比一般人家要富裕得多，她從小到大享受着充分的父愛母愛，但與社會，特别是基層社會接觸很少。”

　　“對對，極對！她從沒對我說過家裡的情況，事實上從未說過任何關于她自己的情況，但我想應該是那樣的！”

　　“下面的推測就是猜測了，錯了你告訴我――她喜歡穿那種，怎麼說呢，素雅的衣服，在她這種年齡的女孩子來說，顯得稍微素了些。”羅輯呆呆地連連點頭，“但總有很潔白的部分，比如襯衣呀領子呀什麼的，與其餘深色的部分形成挺鮮明的對比。”

　　“大史啊，你……”羅輯用近乎崇敬的目光看着大史說。

　　史強揮手制止他說下去，“最後一點：她個子不高，一米六左右吧，身材很……怎麼形容來着，纖細，一陣風就能刮跑的那種，是以這個兒也不顯得低……當然還能想出很多，應該都差不離吧。”

　　羅輯像要給史強跪下似的，“大史，我五體投地！你，福爾摩斯再世啊！”

　　大史站起來，“那我去電腦上畫了。”

　　大史成功地将一個NP問題加上了若幹限制條件，最後找到了這個女孩兒，名字叫莊顔，隻是比幻想中的“她”多了淡淡的憂傷。

　　2. 繞過問題

　　在碰到難題時，除了積極面對外，我們也應當思考一下，問題是否真的有解決的必要？是否可以繞過問題直指目标？

　　在第一次世界大戰後，法國為了防止德軍入侵而在其東北邊境地區構築起了一道有鋼筋混凝土建造而成的防線，防線内部擁有各式大炮、壕溝、堡壘、廚房、發電站、醫院、工廠等，通道四通八達，較大的工事中還有有軌電車通道，這就是著名的馬其諾防線。馬其諾防線從1928年起開始建造，1940年才基本建成，造價50億法郎。這道“完全防禦”軍事思想的防線被譽為“不可攻破的防線”。結果大家都知道了，德國人沒有對着馬其諾防線死磕，而是繞過防線，率領28個師穿入阿登山區進攻比利時、荷蘭和盧森堡，還沒等法國人來得及反應，德國軍隊就兵臨巴黎城下，法國投降。

　　德國人的目标是占領法國，馬奇諾防線是達到目标途中的一個難題，這個難題被輕易地繞開了。很多時候，“搬家”或許比“移山”更有效。

　　3. 轉換問題

　　另一種值得一試的辦法是把待解決的難題轉換成另一個能夠解決的問題。

　　密碼疑雲 (3)——詳解RSA的加密與解密 中，Mallory并沒有嘗試破解“芒砀山系統”，而是通過一系列社會工程學的知識騙取了密碼，進而輕易進入“号稱能夠安全運作100年”的系統。

　　最小二乘法（2）——多項式函數能夠拟合非線性問題原理 中，我們介紹了泰勒展開，它将一個難以處理的積分轉換成了無數個易于處理的簡單積分，使用極限的思想求解，達到化質為量的目的。

　　網絡流(3)——找到最小st-剪切 中，我們将多源點的押糧問題轉換成了标準的最大流問題，用已掌握的知識求解。

　　4. 退而求其次

　　如果在通向目标的途中一定要解決某個NP困難問題，那麼 搜尋的政策（2）——貪心政策、A*搜尋詳解(1)——通往基地的最短路線 介紹的一些有啟發性質的算法或許會提供一些參考；退而求其次(2)——遺傳算法 的遺傳算法還告訴我們，在必要的時候應當放棄尋找最優解，轉而尋找可以接受的較好解。如果考不上清華、北大，其他“985”也不是不可接受。

　　5. 依賴計算機的高速運算

　　對于八皇後問題，1854年在柏林的象棋雜志上不同的作者發表了40種不同的解。今天，我們可以通過近乎蠻力的搜尋找到全部的92種解。

　　1946年誕生的ENIAC，每秒隻能進行300次各種運算或5000次加法。

　　2019年，美國的“頂點”，取代“神威太湖之光” 成為“世界第一計算機”，其預算速度為20億億次/每秒。

　　75年間，計算機的速度已經得到了極大的提升，雖然NP問題仍然是NP問題，但是技術的進步給了我們一戰的勇氣，讓我們可以使用蠻力法處理一些中等規模的問題。

　　處理器運算速度的提升帶給了我們更多的可能性。Square公司于1997年在PS上發行的角色扮演類遊戲《最終幻想7》，盡管劇情優秀，但畫質着實“感人”，但是在當年，那種充滿方塊感的畫面仍然是PS平台上不可逾越的經典。2019年6月10日，Square Enix公司在美國洛杉矶舉辦了《最終幻想7》音樂會，宣布遊戲《最終幻想7：重制版》将于2020年3月3日登陸PS4平台，并公布了遊戲的宣傳片。在宣傳片中，遊戲畫面十分華麗，人物幾可亂真。

　　計算機性能的提升可以幫我們解決相當一部分問題，這樣看來，蠻力法也不是那麼一無是處。

　　6. 嘗試NC搜尋

　　随着多核技術和分布式計算的發展，我們似乎更有勇氣碰觸一些過去的禁地。我們把那些能夠通過并行計算快速找到答案的搜尋稱為NC搜尋。然而遺憾的是，NP問題的規模也在擴大，我們今天面對的問題也比過去複雜得多，是以NC也不是萬能藥。

　　盡管在未來，NP是否能用NC仍然不得而知，但是NC搜尋可以幫我們快速解決一些小規模的NP問題，或者在可接受的時間解決一些中等規模的NP問題。

　　7. 打乒乓球去吧

　　當上述方案都無效時，大概可以打乒乓球去了。

　　其實P/NP問題并不僅僅是一道數學難題，它更像是一種指導思想，一種根據問題的困難程度将問題分類的工具。當面對一個NP完全問題時，我們知道沒有一個能夠在所有情況下都解決該問題的算法，我們要做的并不死磕硬打，而是找到某些替代方法，做出某些“退而求其次”或“不得已而為之”的選擇。

如果P=NP

　　美國科幻作家艾薩克·阿西莫夫的小說《永恒的終結》講訴了一個關于時空的神奇故事：27世紀，人類在掌握時間旅行技術後，創造了“時空壺”，并成立了一個叫做“永恒時空”的組織，在每個時代的背後，默默地守護着人類社會的發展。這一系列功勞都歸功于24世紀的一個名叫馬蘭松的偉大科學家，正是他發明了時間力場，進而創造了“時空壺”。盡管馬蘭松的後人們一直在使用“時空壺”，但并不明白它的運作原理，因為作為“時間力場”理論基礎的“列斐伏爾方程”在24世紀還沒有出現！随着劇情的推進，最終揭示了完整的“因果鍊”——來自27世紀的庫珀為24世紀帶去了“列斐伏爾方程”，并從此留在24世紀，最終改名為馬蘭松。

　　歐幾裡得在著作《幾何原本》時不曾想到會有内角和不等于180°的三角形。1830年前後，俄國數學家羅巴切夫斯基發表了關于非歐幾何的理論，即後來的羅氏幾何。在這種幾何裡，羅巴切夫斯基平行公理替代了歐幾裡得平行公理，即存在直線a及不在a上的一點A，過A點至少有兩條直線與a共面且不相交。由此可演繹出一系列全無沖突的結論，并且可以得出三角形的内角和小于180°。正是羅氏幾何啟發了愛因斯坦，成為發現廣義相對論的基礎。

　　對于NP問題來說，強調的是“不确定”是否在能做多項式時間内解決。随着科技的發展，過去“不确定”的問題在未來未必不可觸及。既然P/NP問題的解決可能有賴于大幅度提升的理論和技術，那麼我們不妨把希望寄托于未來，暢想一下P=NP的世界。

　　如果P=NP，基于NP完全問題的密碼大廈将會瞬間傾塌，安全體系将會被重構；如果P=NP，電子遊戲将不再局限于策劃師設計好的劇本，而是像《安德的遊戲》中的心理測試遊戲一樣，根據安德的選擇做出自行演化；如果P=NP，DNA密碼将被破解，生命之謎将被解開，人類将得到新一輪的進化；如果P=NP，機器人将被賦予更進階的智能，《銀河帝國》将不再是幻想……到了那時，人類文明應當通向何方呢？

　　作者：我是8位的

　　出處：http://www.cnblogs.com/bigmonkey