一. QQ圖
分位數圖示法(Quantile Quantile Plot,簡稱 Q-Q 圖)
統計學裡Q-Q圖(Q代表分位數)是一個機率圖,用圖形的方式比較兩個機率分布,把他們的兩個分位數放在一起比較。首先選好分位數間隔。圖上的點(x,y)反映出其中一個第二個分布(y坐标)的分位數和與之對應的第一分布(x坐标)的相同分位數。是以,這條線是一條以分位數間隔為參數的曲線。如果兩個分布相似,則該Q-Q圖趨近于落在y=x線上。如果兩分布線性相關,則點在Q-Q圖上趨近于落在一條直線上,但不一定在y=x線上。Q-Q圖可以用來可在分布的位置-尺度範疇上可視化的評估參數。
從定義中可以看出Q-Q圖主要用于檢驗資料分布的相似性,如果要利用Q-Q圖來對資料進行正态分布的檢驗,則可以令x軸為正态分布的分位數,y軸為樣本分位數,如果這兩者構成的點分布在一條直線上,就證明樣本資料與正态分布存線上性相關性,即服從正态分布。
二. PP圖
P-P圖是根據變量的累積機率對應于所指定的理論分布累積機率繪制的散點圖,用于直覺地檢測樣本資料是否符合某一機率分布。如果被檢驗的資料符合所指定的分布,則代表樣本資料的點應當基本在代表理論分布的對角線上。
由于P-P圖和Q-Q圖的用途完全相同,隻是檢驗方法存在差異。要利用QQ圖鑒别樣本資料是否近似于正态分布,隻需看QQ圖上的點是否近似地在一條直線附近,而且該直線的斜率為标準差,截距為均值.
用QQ圖還可獲得樣本偏度和峰度的粗略資訊.
scipy 畫Q-Q圖
fig = plt.figure()
res = stats.probplot(train['SalePrice'], plot=plt)
plt.show() 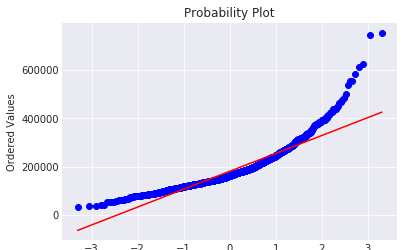
scipy.stats 用法
# -*- coding: utf-8 -*-
from scipy import stats
from numpy import random
# Distributions
# 常用分布可參考本文檔結尾處
# 分布可以使用的方法見下列清單
data=random.normal(size=1000)
stats.norm.rvs(loc=0,scale=1,size=10,random_state=None) # 生成随機數
stats.norm.pdf(-1.96,loc=0,scale=1) # 密度分布函數,畫密度分布圖時使用
stats.norm.cdf(-1.96,loc=0,scale=1) # 累計分布函數,-1.96對應2.5%
stats.norm.sf(-1.96,loc=0,scale=1) # 殘存函數(=1-cdf),-1.96對應97.5%
stats.norm.ppf(0.025,loc=0,scale=1) # 累計分布函數反過來
stats.norm.isf(0.975,loc=0,scale=1) # 殘存函數反過來
stats.norm.interval(0.95,loc=0,scale=1) # 置信度為95%的置信區間
stats.norm.moment(n=2,loc=0,scale=1) # n階非中心距,n=2時是方差
stats.norm.median(loc=0,scale=1) # Median of the distribution.
stats.norm.mean(loc=0,scale=1) # Mean of the distribution.
stats.norm.var(loc=0,scale=1) # Variance of the distribution.
stats.norm.std(loc=0,scale=1) # Standard deviation of the distribution.
stats.norm.fit(data) # fit 估計潛在分布的參數
# Statistical functions
stats.describe([1,2,3]) # 傳回多個統計量
stats.gmean([1,2,4]) # 幾何平均數 n-th root of (x1 * x2 * ... * xn)
stats.hmean([2,2,2]) # 調和平均數 n / (1/x1 + 1/x2 + ... + 1/xn)
stats.trim_mean([1,2,3,5],0.25) # 砍頭去尾均值,按比例砍
stats.sem(data) # Calculates the standard error of the mean
stats.mode([1,1,2]) # 衆數
stats.skew(data) # 偏度
stats.kurtosis(data) # 峰度
stats.moment(data,moment=3) # n階中心矩,3階就是偏度,4階就是峰度
stats.skewtest(data) # 檢驗偏度是否符合正态分布的偏度
stats.kurtosistest(data) # 檢驗峰度是否符合正态分布的峰度
stats.normaltest(data) # 檢驗是否符合正态分布
stats.variation([1,2,3]) # 變異系數(=std/mean*100%)
stats.find_repeats([1,1,2,2,3]) # 重複值查找
stats.itemfreq([1,1,2,2,3]) # 頻次統計
stats.percentileofscore([1,2,3,4,5],2) # 傳回數值的分位數
stats.scoreatpercentile([1,2,3,4,5],80,interpolation_method="lower") # 傳回分位數對應的數值
stats.bayes_mvs(data) # 傳回均值/方差/标準差的貝葉斯置信區間
stats.iqr([1,2,3,4,5],rng=(25,75)) # 計算 IQR
stats.zscore(data) # 計算 zscore
stats.f_oneway(data,data+data,data+data+data) # 單因素方差分析,參數是(樣本組1,樣本組2,樣本組3)
stats.pearsonr(data,data+data) # 皮爾森相關系數
stats.spearmanr(data,data+data) # 斯皮爾曼秩相關系數
stats.kendalltau(data,data+data) # 肯德爾相關系數
stats.pointbiserialr([1,1,1,0,0,0],[1,2,3,4,5,6]) # 點二系列相關,第一個變量需要是二分類變量
stats.linregress(data,data+data) # 線性最小二乘回歸
stats.ttest_1samp(data,popmean=0) # 單樣本 t-檢驗: 檢驗總體平均數的值
stats.ttest_ind(data,data+data) # 雙樣本 t-檢驗: 檢驗不同總體的差異
stats.ttest_rel(data,data+data) # 配對樣本 t-檢驗
stats.ttest_ind_from_stats(mean1=0,std1=1,nobs1=100,mean2=10,std2=1,nobs2=150,equal_var=True) # 根據統計量做 t-檢驗
stats.wilcoxon(data,data+data) # 一種非參數的配對樣本檢驗。t-檢驗假定高斯誤差。可以使用威爾科克森符号秩檢驗, 放松了這個假設
stats.kstest(data,'norm') # Kolmogorov–Smirnov檢驗: 檢驗單一樣本是否服從某一預先假設的特定分布
stats.ks_2samp(data,data+data) # 檢測兩樣本分布是否相同
stats.ranksums(data,data+data) # Wilcoxon rank-sum statistic 檢測兩樣本分布是否相同
stats.chisquare(data,data) # 卡方檢驗,第一個參數是樣本分布,第二個參數是期望分布
# Circular statistical functions
# 适用于環形資料,如時間(60分鐘一圈),角度(360度一圈)
# 例如 0度 與 360度 的均值應該是 0度
stats.circmean([0,360],high=0,low=360) # 均值
stats.circvar([0,360],high=0,low=360) # 方差
stats.circstd([0,360],high=0,low=360) # 标準差
# Contingency table functions
# 列聯表
stats.chi2_contingency([[10,10,20],[20,20,20]],lambda_="log-likelihood") # 卡方檢驗,n*m的列聯表,每個格子樣本數要大于5,lambda_預設皮爾森
stats.fisher_exact([[8,2],[1,5]],alternative="two-sided") # 費舍爾精确檢驗,2*2的列聯表,alternative:two-sided,less,greater
stats.contingency.expected_freq([[10,10,20],[20,20,20]]) # 傳回列聯表的期望頻次(各變量獨立時的預期頻次)
import numpy as np; stats.contingency.margins(np.array([[10,10,20],[20,20,20]]))# 傳回列聯表的行列和
# Plot-tests
# 圖檢驗:probplot與Q-Q圖的差異:P-P圖是用分布的累計比,而Q-Q圖用的是分布的分位數來做檢驗
import matplotlib.pyplot as plt
data=random.normal(loc=0,scale=1,size=500)
stats.probplot(data,dist=stats.norm,sparams=(0,1),plot=plt) # P-P圖(probability plot),參數sparams傳的是均值與标準差
stats.boxcox_normplot(abs(data),-3,3,plot=plt) # 不知幹啥用,Compute parameters for a Box-Cox normality plot
stats.ppcc_plot(data,-3,3,dist=stats.norm,plot=plt) # 不知幹啥用,Calculate and optionally plot probability plot correlation coefficient.
stats.ppcc_max(data,dist=stats.norm) # 不知幹啥用,傳回 PPCC 取最大時對應的位置
# Univariate and multivariate kernel density estimation
# 核密度估計用于估計未知的密度函數,屬於非參數檢驗方法之一
stats.gaussian_kde([data,data+random.normal(size=500)]) # 不知幹啥用,Representation of a kernel-density estimate using Gaussian kernels.
""" ---------------------------------------------------------------------------------------------------------
所有分布都是 rv_continuous(連續型分布) 與 rv_discrete(離散型分布) 的執行個體
rv_continuous([momtype, a, b, xtol, ...]) A generic continuous random variable class meant for subclassing.
rv_discrete([a, b, name, badvalue, ...]) A generic discrete random variable class meant for subclassing.
rv_histogram(histogram, *args, **kwargs) Generates a distribution given by a histogram.
Continuous distributions 連續型分布
alpha An alpha continuous random variable.
beta A beta continuous random variable.
chi2 A chi-squared continuous random variable.
f An F continuous random variable.
gamma A gamma continuous random variable.
lognorm A lognormal continuous random variable.
ncx2 A non-central chi-squared continuous random variable.
ncf A non-central F distribution continuous random variable.
nct A non-central Student’s T continuous random variable.
norm A normal continuous random variable.
pareto A Pareto continuous random variable.
t A Student’s T continuous random variable.
uniform A uniform continuous random variable.
wald A Wald continuous random variable.
……
Multivariate distributions 多元分布
multivariate_normal A multivariate normal random variable.
matrix_normal A matrix normal random variable.
multinomial A multinomial random variable.
random_correlation A random correlation matrix.
……
Discrete distributions 離散型分布
binom A binomial discrete random variable.
hypergeom A hypergeometric discrete random variable.
nbinom A negative binomial discrete random variable.
poisson A Poisson discrete random variable.
randint A uniform discrete random variable. 參考:
Q-Q圖簡介
學習-Python-資料分析&資料挖掘-4 SciPy.stats
如果這篇文章幫助到了你,你可以請作者喝一杯咖啡