樹狀數組:
一共需要三個函數:
①lowbit(int x)
②add(int x,int p)
③query(int x)
1.動态求連續區間和
給定 n 個數組成的一個數列,規定有兩種操作,一是修改某個元素,二是求子數列 [a,b]的連續和。
輸入格式
第一行包含兩個整數 n 和 m,分别表示數的個數和操作次數。
第二行包含 n 個整數,表示完整數列。
接下來 m 行,每行包含三個整數 k,a,b (k=0,表示求子數列[a,b]的和;k=1,表示第 a 個數加 b)。
數列從 1 開始計數。
輸出格式
輸出若幹行數字,表示 k=0時,對應的子數列 [a,b]的連續和。
資料範圍
1≤n≤100000
1≤m≤100000
1≤a≤b≤n
輸入樣例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
輸出樣例:
11
30
35
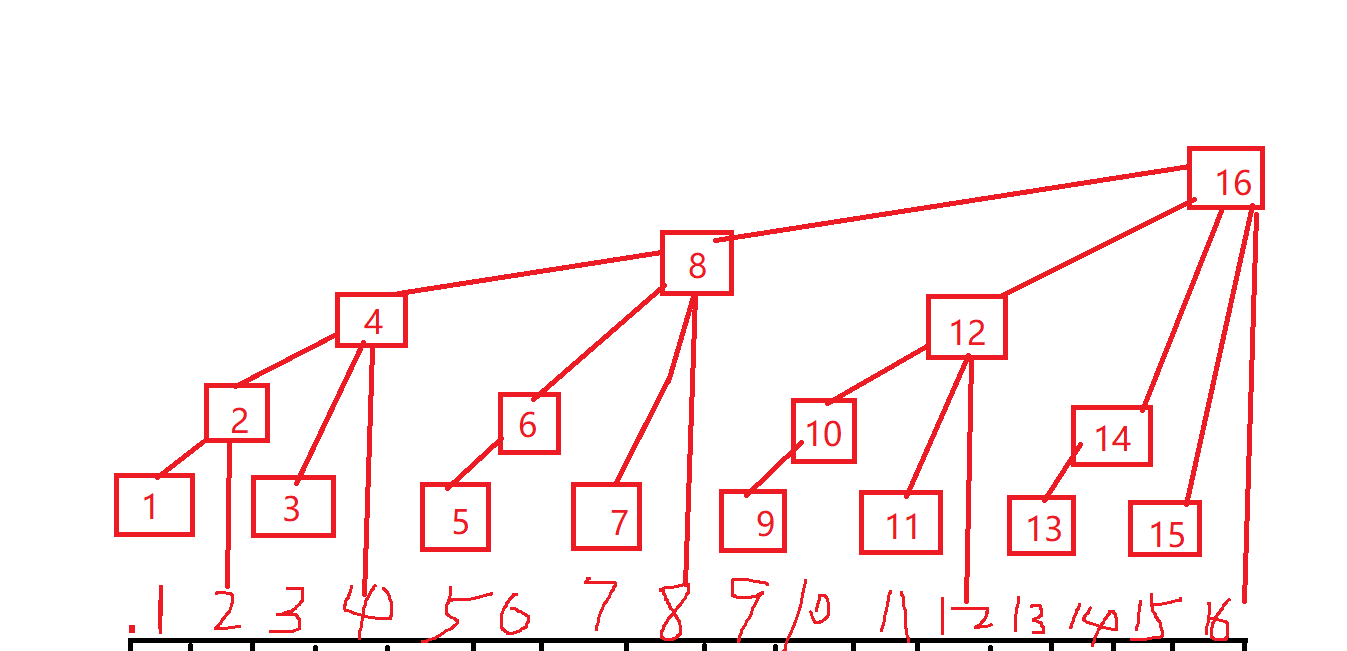
解題思路:一道入門級題目,利用樹狀數組來進行求解
代碼:
#include<iostream>
#include<algorithm>
using namespace std;
const int N=100010;
int n,m;
int a[N],tr[N];
int lowbit(int x)
{
return x&-x;
}
void add(int x,int p)
{
for(int i=x;i<=n;i+=lowbit(i))
tr[i]+=p;
}
int query(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i))
ans+=tr[i];
return ans;
}
int main()
{
int i,j,x,y,k;
cin>>n>>m;
for(i=1;i<=n;i++)
cin>>a[i];
for(i=1;i<=n;i++)
add(i,a[i]);
for(i=1;i<=m;i++)
{
cin>>k>>x>>y;
if(k==1)
{
add(x,y);
}
else
{
cout<<query(y)-query(x-1)<<endl;
}
}
return 0;
} 2.數星星
天空中有一些星星,這些星星都在不同的位置,每個星星有個坐标。
如果一個星星的左下方(包含正左和正下)有 kk 顆星星,就說這顆星星是 kk 級的。
例如,上圖中星星 5 是 3級的(1,2,4 在它左下),星星 2,4 是 1 級的。
例圖中有 1 個 0 級,2 個 1 級,1 個 2 級,1 個3 級的星星。
給定星星的位置,輸出各級星星的數目。
換句話說,給定 N 個點,定義每個點的等級是在該點左下方(含正左、正下)的點的數目,試統計每個等級有多少個點。
第一行一個整數 N,表示星星的數目;
接下來 N 行給出每顆星星的坐标,坐标用兩個整數 x,y 表示;
不會有星星重疊。星星按 y 坐标增序給出,y 坐标相同的按 x 坐标增序給出。
N 行,每行一個整數,分别是 0 級,1 級,2 級,……,N−1 級的星星的數目。
1≤N≤15000,
0≤x,y≤32000
5
1 1
5 1
7 1
3 3
5 5
1
2
1
1
0
解題思路:這道題隻需要根據x坐标來建立樹狀數組,求由于樹狀數組下标從1開始,故在讀入時x坐标要加1,先統計在該星星前有多少個星星,在進行add操作,加上這顆星星
類似于求小于x的橫坐标個數的字首和。
代碼:
#include<iostream>
#include<cstdio>
using namespace std;
const int N=32010;
int tr[N],level[N];
int lowbit(int x)
{
return x&-x;
}
void add(int x,int t)
{
for(int i=x;i<N;i+=lowbit(i))
tr[i]+=t;
}
int query(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i))
ans+=tr[i];
return ans;
}
int main()
{
int i,j,n,x,y;
cin>>n;
for(i=0;i<n;i++)
{
scanf("%d%d",&x,&y);
x++;
level[query(x)]++;
add(x,1);
}
for(i=0;i<n;i++)
printf("%d\n",level[i]);
return 0;
} 線段樹操作
①pushup:用位元組點資訊更新目前節點資訊
②build:在一段區間上初始化線段樹
③modify:修改
④query:查詢
線段樹模拟:
1.動态求連續區間和
線段樹做法:
#include<iostream>
using namespace std;
const int N=100010;
int n,m;
int w[N];
struct node
{
int l,r;
int sum;
}tr[N*4];
void pushup(int u)
{
tr[u].sum=tr[u*2].sum+tr[u*2+1].sum;
}
void build(int u,int l,int r)
{
if(l==r)
tr[u]={l,r,w[r]};
else
{
tr[u]={l,r};
int mid=l+r>>1;
build(u*2,l,mid),build(u*2+1,mid+1,r);
pushup(u);
}
}
int query(int u,int l,int r)
{
if(tr[u].l>=l&&tr[u].r<=r)
return tr[u].sum;
int mid=tr[u].l+tr[u].r>>1;
int sum=0;
if(l<=mid)
sum=query(u*2,l,r);
if(r>mid)
sum+=query(u*2+1,l,r);
return sum;
}
void modify(int u,int x,int v)
{
if(tr[u].l==tr[u].r)
tr[u].sum+=v;
else
{
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid)
modify(u<<1,x,v);
else
modify(u<<1|1,x,v);
pushup(u);
}
}
int main()
{
int i,j,k,x,y;
cin>>n>>m;
for(i=1;i<=n;i++)
cin>>w[i];
build(1,1,n);
while(m--)
{
cin>>k>>x>>y;
if(k==0)
cout<<query(1,x,y)<<endl;
else
modify(1,x,y);
}
return 0;
} 2.數列區間最大值
輸入一串數字,給你 M 個詢問,每次詢問就給你兩個數字 X,Y,要求你說出 X 到 Y 這段區間内的最大數。
第一行兩個整數 N,M 表示數字的個數和要詢問的次數;
接下來一行為 N 個數;
接下來 M 行,每行都有兩個整數 X,Y。
輸出共 M 行,每行輸出一個數。
1≤N≤105,
1≤M≤106
1≤X≤Y≤N
數列中的數字均不超過231−1
10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8
5
8 解題思路:根據線段樹來處理,此時結構體裡應該添加的一個數是maxn,來記錄目前的最大值,在建樹時更新目前樹根的最大值,
在算區間最大值時,先判斷左右是否在區間内,若不在判斷該點的mid與左右區間是否有交集,然後取最大的。
代碼:
#include<iostream>
#include<cstdio>
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int w[N];
struct node
{
int l,r;
int maxn;
}tr[N*4];
void build(int u,int l,int r)
{
if(l==r)
tr[u]={l,r,w[r]};
else
{
tr[u]={l,r};
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
tr[u].maxn=max(tr[u*2].maxn,tr[u*2+1].maxn);
}
}
int query(int u,int l,int r)
{
if(tr[u].l>=l&&tr[u].r<=r)
return tr[u].maxn;
int mid=tr[u].l+tr[u].r>>1;
int ans=INT_MIN;
if(l<=mid)
ans=query(u<<1,l,r);
if(r>mid)
ans=max(ans,query(u<<1|1,l,r));
return ans;
}
int main()
{
int n,m,i;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
scanf("%d",&w[i]);
build(1,1,n);
int l,r;
while(m--)
{
scanf("%d%d",&l,&r);
printf("%d\n",query(1,l,r));
}
return 0;
}