文章目錄
- 前言
- 題目
- 題解
- 正文
-
- NO1:整除比較法(初始思路)
- NO2:KMP解決(核心,重點掌握)
- NO3:超級整除法(參考大佬)
- NO4、超簡潔解法(看看就好)
- 參考文章
前言
哈喽,我是長路,目前剛剛大三,方向是後端也偶爾搗鼓下前端,現在的主語言是Java。之前一大段時間都是在學習web開發的一些技術,就很久沒有進行類似于資料結構、算法之類的學習與刷題,打算這段時間拾起來好好學一學、搞一搞。
這段時間也是機緣巧合看到草帽路飛的部落格,加了自學群,正巧看到部落客組織在群裡組織了leetcode刷題打卡活動,我也就參與進來,為期一個月,打算堅持每天都花一些時間做一些題目,并通過部落格的方式來進行記錄。
目前跟着一個Github倉庫刷題(leetcode):代碼随想錄leetcode刷題,目前為連結清單專題。
題目來源leetcode
leetcode位址:459. 重複的子字元串,難度:簡單。
題目描述(摘自leetcode):
給定一個非空的字元串,判斷它是否可以由它的一個子串重複多次構成。給定的字元串隻含有小寫英文字母,并且長度不超過10000。
示例 1:
輸入: "abab"
輸出: True
解釋: 可由子字元串 "ab" 重複兩次構成。
示例 2:
輸入: "aba"
輸出: False
示例 3:
輸入: "abcabcabcabc"
輸出: True
解釋: 可由子字元串 "abc" 重複四次構成。 (或者子字元串 "abcabc" 重複兩次構成。)
本地調試代碼:
class Solution {
public boolean repeatedSubstringPattern(String s) {
...
}
public static void main(String[] args) {
System.out.println(new Solution().repeatedSubstringPattern("aba"));
}
}
題解
思路: 先自己想思路,有了思路直接code就行,目前送出沒有看題解。
核心點:一個子串重複多次構成、隻含有小寫英文字母、長度不超過10000
思路:
1、确定每次重複的個數,這是我們能夠确定的。例如"abababab",長度為8。那麼每次重複個數情況有1、2、4。(for循環模一下即可判定)
2、直到重複個數之後就好辦了,重新開個for循環從指定位置開始指定長度比較就ok,一旦一組比較下來都相同直接傳回true,否則進行其他重複個數情況二次比較!
代碼:
public boolean repeatedSubstringPattern(String s) {
String subStr = "";
for (int i = 1; i < s.length(); i++) {
//每i個數能夠成對出現
if(s.length() % i == 0){
subStr = s.substring(0,i);
int j = i;
for (; j < s.length(); j+=i) {
if(!Objects.equals(subStr,s.substring(j,j+i))){
break;
}
}
if(j == s.length()){
return true;
}
}
}
return false;
}
同樣與這個思路一緻,将直接取兩個子串方式改為取兩個指針來從左到右進行比較,看下是否有時間上的優化:
- 注釋的内容表示被替換了
public boolean repeatedSubstringPattern(String s) {
// String subStr = "";
for (int i = 1; i < s.length(); i++) {
if(s.length() % i == 0){
// subStr = s.substring(0,i);
int j = i;
for (; j < s.length(); j+=i) {
//左右指針比較
// if(!Objects.equals(subStr,s.substring(j,j+i))){
// break;
// }
/*******直接取子串=>左右連續對比*******/
int subStrCur = 0;
int jCur = j;
while(subStrCur != i){
if(s.charAt(subStrCur) != s.charAt(jCur)){
break;
}
subStrCur++;
jCur++;
}
if(subStrCur != i){
break;
}
/**************/
}
if(j == s.length()){
return true;
}
}
}
return false;
}
效果感覺不咋地,反而比我們使用subString()取字元串來的效率高,現在去看下其他人題解。
思路:利用KMP算法求得next數組,接着通過next數組最後一個元素的指向的最長重複字首位置來進行判斷是否目前字元串是否為重複的子字元串。
舉例:
例1:s="abababab" next[] = [-1, -1, 0, 1, 2, 3, 4, 5]
next數組最後一個位置為5,指向原字元串中的倒數第三個,使用原字元串長度減去該位置-1,8-5-1=2,2就指的是對應子串的長度,接着使用字元串長度進行%,若是=0,表示其為重複子串。公式為:s.length() % (s.length() - targetPos - 1) == 0
例2:s="ababcddc" next=[-1, -1, 0, 1, -1, -1, -1, -1]
最後位置為-1,直接判定沒有重複字元串。
例3:s="ababcdab" next[] = [-1, -1, 0, 1, -1, -1, 0, 1]
最後位置為1,同理代入,8%(8-1-1)=2,沒有整%,是以直接判斷沒有
代碼:時間複雜度O(n)
public int getNext(String s) {
//KMP求得next數組
int next[] = new int[s.length()];
int j = -1;
next[0] = -1;
for (int i = 1; i < s.length(); i++) {
while (j >= 0 && s.charAt(i) != s.charAt(j + 1)) {
j = next[j];
}
if (s.charAt(i) == s.charAt(j + 1)) {
j++;
}
next[i] = j;
}
return next[s.length() - 1];
}
public boolean repeatedSubstringPattern(String s) {
//使用KMP取到最後一個元素重複元素字首位置
int targetPos = getNext(s);
if (targetPos == -1) {
return false;
}
if (s.length() % (s.length() - targetPos - 1) == 0) {
return true;
}
return false;
}
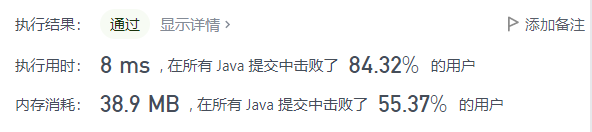
使用KMP最後的執行耗時才擊敗了62%的人,接着就去看了看大佬的代碼,真的是特别特别巧妙!
思路:相對于NO1的整除法,中間有很多沒必要二次比較的情況,并且我是從小數重複串進行一一比對的,這裡使用大數重複串比較,并且省去了一些沒必要重複比較的情況。
假設某個字元串長度為8,按照正常思路順序,先取最長重複串長度為4個4個比較、失敗取2個2個、失敗再取1個1個。
其實後面的兩次就是沒有必要的,我們舉個例子:"abababac"
①abab abac (失敗)
②ab ab ab ac (失敗)
③a b a b a b b a c (失敗)
仔細看第二步,假設它是重複串組成ab ab ab ab,那麼就必然就有abab abab判斷成功,那麼①失敗,下面的②③比較自然沒有必要了。其規律就可以找到凡是某個最大子串比對失敗,那麼其整除的情況(也就是②③)直接可以省略掉。
上面說明了沒必要重複比較的情況,下面再舉一個長度為6的例子:"ababab"
①aba bab (失敗)
②ab ab ab (成功)
對于該種情況,第②步是不用被省略的,因為第一組最大重複數量為3,其并不能整除2,那麼對重複長度為2的自然會進行一一比較,這裡就有一個問題,我們該如何進行比較?上面長度為6的有三組,難道要一個一個進行比?從大佬的代碼中我又看到了解答,所有任意情況隻要比較1次即可,對于②中取出abab abab這兩個,剛開始我也賊蒙蔽,不過之後就感歎其妙的地方了。
重複長度2,第一組[0,6-2-1]=>[0,3] 第二組[2,6-1]=>[2-5],假設三組子字元串都先相同,那麼任意兩組之和也必然相同,借助這個要點,我們即可将多組比較化為2組比出結果。
public boolean repeatedSubstringPattern2(String s) {
int len = s.length();
int parts = 2;//從2開始,之後取子串len/2、len/3,保證子串從最大長度開始進行比較重複
int noRepeatLen = len;
while (noRepeatLen > 1) {
if (noRepeatLen % parts == 0) {
int k = len / parts;//子串長度
//取出兩組進行比較
if (Objects.equals(s.substring(0, len - k), s.substring(k))) {
return true;
}
//去除重複的整除情況,在除數上進行操作
noRepeatLen /= parts;
while (noRepeatLen % parts == 0) {
noRepeatLen /= parts;
}
}
parts++;
}
return false;
}
好家夥,兩行解決?還是很妙的。舉兩個例子就可以看懂了。
思路:
① s="abac" 不重複情況 "ababca"
s+s = "abacabac",去頭去尾"bacaba"
② s="abab"
s+s = "abababab",去頭去尾"bababa" √
③ s="aaaa"
s+s = "aaaaaaaa",去頭去尾"aaaaaa" √
這種方式很巧妙,通過拼接方式去頭去尾看其中是否存在原字元串。若是有重複的必然拼接中有對應重複的!
public boolean repeatedSubstringPattern(String s) {
String str = s + s;
return str.substring(1, str.length() - 1).contains(s);
}