二叉搜尋樹隻有保持平衡時其查找效率才會高。
要保持二叉搜尋樹的平衡不是一件易事。不過還是有一些非常經典的辦法可以做到,其中最好的方法就是将二叉搜尋樹實作為AVL樹。
AVL樹得名于它的發明者 G.M. Adelson-Velsky 和 E.M. Landis,他們在 1962 年的論文 "An algorithm for the organization of information" 中發表了它。AVL樹是一種特殊類型的二叉樹,它的每個結點都儲存一份額外的資訊:結點的平衡因子。
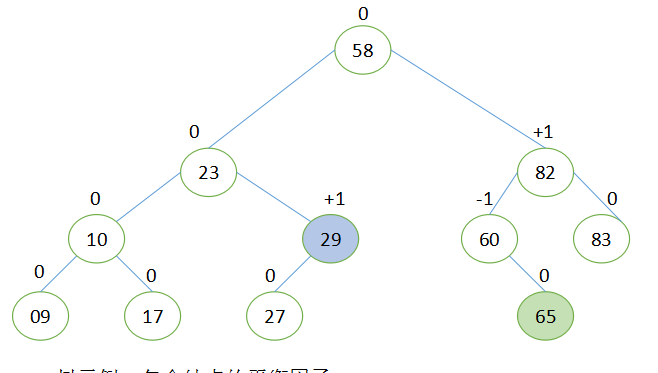
結點的平衡因子 = 左子樹的高度 - 右子樹的高度
插入和删除操作都會導緻AVL樹的自我調整(自我平衡),使得所有結點的平衡因子保持為+1、-1或0。
當子樹的根結點的平衡因子為+1時,它是左傾斜的(left-heavy)。
當子樹的根結點的平衡因子為 -1時,它是右傾斜的(right-heavy)。
一顆子樹的根結點的平衡因子就代表該子樹的平衡性。
保持所有子樹幾乎都處于平衡狀态,AVL樹在總體上就能夠基本保持平衡。
AVL樹的旋轉
旋轉操作用來重新平衡樹的某個部分。通過重新安排結點 ,使結點之間的關系始終保持左子結點小于父結點,父結點小于右子結點。使得該樹仍然是一顆二叉搜尋樹。旋轉過後,旋轉子樹中的所有結點的平衡因子都為+1、-1或0。
AVL樹的旋轉類型有4種, 分别是LL(left-left)旋轉、LR(left-right)旋轉、RR(right-right)旋轉和RL(right-left)旋轉。
為友善了解在何時執行哪一種旋轉,設x代表剛插入AVL樹中的結點,設A為離x最近且平衡因子更改為2的絕對值的祖先。可以歸納為下面4種處理情況:
LL旋轉
如下圖所示,當x位于A的左子樹的左子樹上時,執行LL旋轉。
設left為A的左子樹,要執行LL旋轉,将A的左指針指向left的右子結點,left的右指針指向A,将原來指向A的指針指向left。
旋轉過後,将A和left的平衡因子都改為0。所有其他結點的平衡因子沒有發生變化。
LR旋轉
當x位于A的左子樹的右子樹上時,執行LR旋轉。
設left是A的左子結點,并設A的子孫結點grandchild為left的右子結點。
要執行LR旋轉,将left的右子結點指向grandchild的左子結點,grandchild的左子結點指向left,A的左子結點指向grandchild的右子結點,再将grandchild的右子結點指向A,最後将原來指向A的指針指向grandchild。
執行LR旋轉之後,調整結點的平衡因子取決于旋轉前grandchild結點的原平衡因子值。
如果grandchild結點的原始平衡因子為+1,就将A的平衡因子設為-1,将left的平衡因子設為0。
如果grandchild結點的原始平衡因子為0,就将A和left的平衡因子都設定為0。
如果grandchild結點的原始平衡因子為-1,就将A的平衡因子設定為0,将left的平衡因子設定為+1。
在所有的情況下,grandchild的新平衡因子都是0。所有其他結點的平衡因子都沒有改變。
RR旋轉
當x位于A的左子樹的右子樹上時,執行RR旋轉。
RR旋轉與LL旋轉是對稱的關系。
設A的右子結點為Right。要執行RR旋轉,将A的右指針指向right的左子結點,right的左指針指向A,原來指向A的指針修改為指向right。
完成旋轉以後,将A和left的平衡因子都修改為0。所有其他結點的平衡因子都沒有改變。
RL旋轉
當x位于A的右子樹的左子樹上時,執行RL旋轉。
RL旋轉與LR旋轉是對稱的關系。
設A的右子結點為right,right的左子結點為grandchild。要執行RL旋轉,将right結點的左子結點指向grandchild的右子結點,将grandchild的右子結點指向right,将A的右子結點指向grandchild的左子結點,将grandchild的左子結點指向A,最後将原來指向A的指針指向grandchild。
執行RL旋轉以後,調整結點的平衡因子取決于旋轉前grandchild結點的原平衡因子。這裡也有三種情況需要考慮:
如果grandchild的原始平衡因子值為+1,将A的平衡因子更新為0,right的更新為-1;
如果grandchild的原始平衡因子值為 0,将A和right的平衡因子都更新為0;
如果grandchild的原始平衡因子值為-1,将A的平衡因子更新為+1,right的更新為0;
在所有情況中,都将grandchild的新平衡因子設定為0。所有其他結點的平衡因子不發生改變。
來源:https://www.cnblogs.com/idreamo/p/8308336.html