[經典算法] 堆排序

題目說明：

堆排序(Heapsort)是指利用堆積樹（堆）這種資料結構所設計的一種排序算法，它是選擇排序的一種。排序n 個項目要

Ο

(n log n)次比較。

題目解析：

1、堆

堆實際上是一棵完全二叉樹，在第一個元素的索引為0的情形中滿足特性：

性質一：索引為i的左孩子的索引是 (2*i+1);

性質二：索引為i的左孩子的索引是 (2*i+2);

性質三：索引為i的父結點的索引是 int((i-1)/2);

最大堆：任何父節點的關鍵字不小于其左右孩子節點的關鍵字（Key[i]>=Key[2i+1]&&key>=key[2i+2]）;

最小堆：任何父節點的關鍵字不小于其左右孩子節點的關鍵字（Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]）;

由上述性質可知最大堆的堆頂的關鍵字肯定是所有關鍵字中最大的，最小堆的堆頂的關鍵字是所有關鍵字中最小的。

如下面最大堆和最小堆

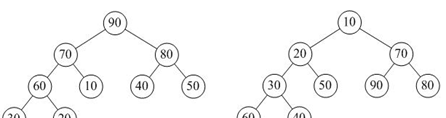
2、堆排序

利用最大堆(最小堆)堆頂記錄的是最大關鍵字(最小關鍵字)這一特性，使得每次從無序中選擇最大記錄(最小記錄)變得簡單。

其基本思想為(最大堆)：

1)将初始待排序關鍵字序列(R1,R2….Rn)建構成大頂堆，此堆為初始的無序區；

2)将堆頂元素R[1]與最後一個元素R[n]交換，此時得到新的無序區(R1,R2,……Rn-1)和新的有序區(Rn),且滿足R[1,2...n-1]<=R[n];

3)由于交換後新的堆頂R[1]可能違反堆的性質，是以需要對目前無序區(R1,R2,……Rn-1)調整為新堆，然後再次将R[1]與無序區最後一個元素交換，得到新的無序區(R1,R2….Rn-2)和新的有序區(Rn-1,Rn)。不斷重複此過程直到有序區的元素個數為n-1，則整個排序過程完成。

操作過程如下：

1)初始化堆：将R[1..n]構造為堆；

2)将目前無序區的堆頂元素R[1]同該區間的最後一個記錄交換，然後将新的無序區調整為新的堆。

是以對于堆排序，最重要的兩個操作就是構造初始堆和調整堆，其實構造初始堆事實上也是調整堆的過程，隻不過構造初始堆是對所有的非葉節點都進行調整。

程式代碼：

#include <gtest/gtest.h>
#include <algorithm>
using namespace std;

#define M_PARENT(i)        (i)/2
#define M_LEFT(i)        2*(i)+1
#define M_RIGHT(i)        2*(i+1)

template<typename T>
void MaxHeapify(T* data, int index, int len)
{
    int l = M_LEFT(index);
    int r = M_RIGHT(index);
    int largest;

    if (l < len && data[l] > data[index])
    {
        largest = l;
    }
    else
    {
        largest = index;
    }

    if (r < len && data[r] > data[largest])
    {
        largest = r;
    }

    if (largest != index)
    {
        T tmp = data[largest];
        data[largest] = data[index];
        data[index] = tmp;

        MaxHeapify(data, largest, len);
    }
}

template<typename T>
void BuildMaxHeap(T* data, int len)
{
    if (!data || len <= 1)
        return;

    for (int i=len/2 + 1; i>=0; --i)
    {
        MaxHeapify(data,i,len);
    }
}

template<typename T>
void HeapSort(T* data, int len)
{
    if (!data || len <= 1)
    {
        return;
    }

    BuildMaxHeap(data, len);

    for (int i=len-1; i>=1; --i)
    {
        T tmp = data[0];
        data[0] = data[i];
        data[i] = tmp;

        MaxHeapify(data,0,--len);
    }
}

// Helper function
template<typename T>
void ShowElem(T& val)
{
    cout << val << " ";
}

template<typename T>
bool Validate(T* data, int len)
{
    for (int i=0; i < len-1; ++i)
    {
        if (data[i] > data[i+1])
        {
            return false;
        }
    }

    return true;
}

TEST(Algo, tHeapSort)
{
    int d1[] = {2,8,7,1,3,5,6,4};
    HeapSort(d1, 8);
    for_each(d1, d1+8, ShowElem<int>);    
    ASSERT_TRUE(Validate(d1,8));    
    cout << endl;

    int d2[] = {2};
    HeapSort(d2, 1);
    for_each(d2, d2+1, ShowElem<int>);
    ASSERT_TRUE(Validate(d2,1));
    cout << endl;

    int d3[] = {2,4,5,6,7,5,2,3,5,7,10,111,2,4,5,6,3,4,5};
    HeapSort(d3, 19);
    for_each(d3, d3+19, ShowElem<int>);
    ASSERT_TRUE(Validate(d3,19));
    cout << endl;
}      

運作結果:

參考引用：

http://www.cricode.com/2001.html

http://www.cnblogs.com/kaituorensheng/archive/2013/02/22/2922970.html

  
             
  看書、學習、寫代碼