-----------我最近在 LeetCode 上做到兩道非常有意思的題目,382 和 398 題,關于水塘抽樣算法(Reservoir Sampling),本質上是一種随機機率算法,解法應該說會者不難,難者不會。
我第一次見到這個算法問題是谷歌的一道算法題:給你一個未知長度的連結清單,請你設計一個算法,隻能周遊一次,随機地傳回連結清單中的一個節點。
這裡說的随機是均勻随機(uniform random),也就是說,如果有
n
1/n
,不可以有統計意義上的偏差。
一般的想法就是,我先周遊一遍連結清單,得到連結清單的總長度
n
[1,n]
之間的随機數為索引,然後找到索引對應的節點,不就是一個随機的節點了嗎?
但題目說了,隻能周遊一次,意味着這種思路不可行。題目還可以再泛化,給一個未知長度的序列,如何在其中随機地選擇
k
個元素?想要解決這個問題,就需要著名的水塘抽樣算法了。
PS:我認真寫了 100 多篇原創,手把手刷 200 道力扣題目,全部釋出在labuladong的算法小抄,持續更新。建議收藏,按照我的文章順序刷題,掌握各種算法套路後投再入題海就如魚得水了。
算法實作
先解決隻抽取一個元素的問題,這個問題的難點在于,随機選擇是「動态」的,比如說你現在你有 5 個元素,你已經随機選取了其中的某個元素
a
作為結果,但是現在再給你一個新元素
b
,你應該留着
a
還是将
b
作為結果呢,以什麼邏輯選擇
a
和
b
呢,怎麼證明你的選擇方法在機率上是公平的呢?
先說結論,當你遇到第
i
個元素時,應該有
1/i
的機率選擇該元素,
1 - 1/i
的機率保持原有的選擇。看代碼容易了解這個思路:
/* 傳回連結清單中一個随機節點的值 */
int getRandom(ListNode head) {
Random r = new Random();
int i = 0, res = 0;
ListNode p = head;
// while 循環周遊連結清單
while (p != null) {
// 生成一個 [0, i) 之間的整數
// 這個整數等于 0 的機率就是 1/i
if (r.nextInt(++i) == 0) {
res = p.val;
}
p = p.next;
}
return res;
} 對于機率算法,代碼往往都是很淺顯的,但是這種問題的關鍵在于證明,你的算法為什麼是對的?為什麼每次以
1/i
的機率更新結果就可以保證結果是平均随機(uniform random)?
證明:假設總共有
n
個元素,我們要的随機性無非就是每個元素被選擇的機率都是
1/n
對吧,那麼對于第
i
個元素,它被選擇的機率就是:
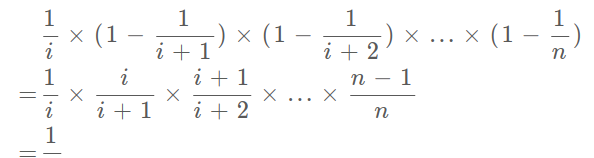
第
i
個元素被選擇的機率是
1/i
,第
i+1
次不被替換的機率是
1 - 1/(i+1)
,以此類推,相乘就是第
i
個元素最終被選中的機率,就是
1/n
。
是以,該算法的邏輯是正确的。
同理,如果要随機選擇
k
個數,隻要在第
i
個元素處以
k/i
的機率選擇該元素,以
1 - k/i
的機率保持原有選擇即可。代碼如下:
/* 傳回連結清單中 k 個随機節點的值 */
int[] getRandom(ListNode head, int k) {
Random r = new Random();
int[] res = new int[k];
ListNode p = head;
// 前 k 個元素先預設選上
for (int j = 0; j < k && p != null; j++) {
res[j] = p.val;
p = p.next;
}
int i = k;
// while 循環周遊連結清單
while (p != null) {
// 生成一個 [0, i) 之間的整數
int j = r.nextInt(++i);
// 這個整數小于 k 的機率就是 k/i
if (j < k) {
res[j] = p.val;
}
p = p.next;
}
return res;
} 對于數學證明,和上面差別不大:
因為雖然每次更新選擇的機率增大了
k
倍,但是選到具體第
i
個元素的機率還是要乘
1/k
,也就回到了上一個推導。
拓展延伸
以上的抽樣算法時間複雜度是 O(n),但不是最優的方法,更優化的算法基于幾何分布(geometric distribution),時間複雜度為 O(k + klog(n/k))。由于涉及的數學知識比較多,這裡就不列出了,有興趣的讀者可以自行搜尋一下。
還有一種思路是基于「Fisher–Yates 洗牌算法」的。随機抽取
k
個元素,等價于對所有元素洗牌,然後選取前
k
個。隻不過,洗牌算法需要對元素的随機通路,是以隻能對數組這類支援随機存儲的資料結構有效。
另外有一種思路也比較有啟發意義:給每一個元素關聯一個随機數,然後把每個元素插入一個容量為
k
的二叉堆(優先級隊列)按照配對的随機數進行排序,最後剩下的
k
個元素也是随機的。
這個方案看起來似乎有點多此一舉,因為插入二叉堆需要 O(logk) 的時間複雜度,是以整個抽樣算法就需要 O(nlogk) 的複雜度,還不如我們最開始的算法。但是,這種思路可以指導我們解決權重随機抽樣算法,權重越高,被随機選中的機率相應增大,這種情況在現實生活中是很常見的,比如你不往遊戲裡充錢,就永遠抽不到皮膚。
最後,我想說随機算法雖然不多,但其實很有技巧的,讀者不妨思考兩個常見且看起來很簡單的問題: