http://www.cnblogs.com/LBSer/p/4020370.html
1 定位背景介紹
一說到定位大家都會想到gps,然而gps定位有首次定位緩慢(具體可以參考之前的博文《LBS定位技術》)、室内不能使用、耗電等缺陷,這些缺陷大大限制了gps的使用。在大多數移動網際網路應用例如google地圖、百度地圖等,往往基于wifi、基站來進行定位。
一般APP在請求定位的時候會上報探測到的wifi信号、基站信号。以wifi為例,手機會探測到周圍各個wifi(mac位址)對應的信号強度(RSSI),即收集到信号向量(<WF1, RSSI1> <WF2, RSSI2> ... <WFN, RSSIN>)。服務端收到用戶端請求後會将信号向量傳給定位引擎,定位引擎會結合這些資訊傳回給服務端定位結果(x, y)、定位精度等資訊,服務端再将此結果傳回給APP。
定位引擎工作基于兩部分:1)大規模的資料收集;2)精細的算法模型。
如圖所示,使用者在請求app尤其是地圖類app的時候,時常會手動開啟GPS定位模式,而這時app會将收集到的基站wifi信号以及gps定位到的坐标發送給服務端,服務端将gps定位坐标(x, y)與信号向量(<WF1, RSSI1> <WF2, RSSI2> ... <WFN, RSSIN>)關聯起來入庫。
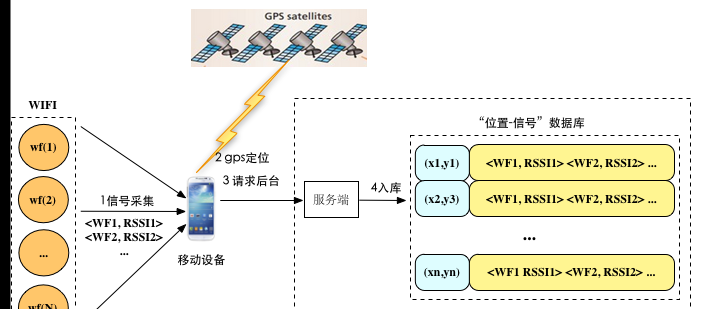
隻要使用者足夠多就能快速積累起大量“位置-信号”資料。如何将這些資料利用起來以實作基于基站wifi的定位将是難題。
通過閱讀文獻,本文設計了一種基于樸素貝葉斯的定位模型。
2 基于樸素貝葉斯的定位模型
我們從機率的角度看待定位問題。
我們目标是計算在已知信号向量m(<WF1, RSSI1> <WF2, RSSI2> ... <WFN, RSSIN>)的情況下,找到一處位置p使得這種情況的可能性最大,目标公式如下:
直接求解該公式非常困難,但我們可以對該公式進行貝葉斯的轉換:
分母P(m)表示信号向量m出現的機率,對于使用者這一次請求來說是常量,是以可以忽略,是以目标公式轉換為:
其中P(p)表示位置p出現的機率,P(m|p)表示在位置p出現信号向量m的機率。簡化起見我們這裡假設位置p出現的機率均等(應該是不均等,比如位置在湖泊中和在市中心大街兩者出現的機率顯然不一樣,以後可以考慮使用此項)。這樣目标公式轉換為:
max(P(m|p))指的是在地理空間上找到一個點p,使得信号向量m出現的機率最大。我們可以窮舉,計算空間上每一個點出現信号向量m的機率,并找出機率最大的點。由于地理空間是二維平面,存在無窮個點,這種計算不可接受,我們可以通過對地理空間進行網格離散化來簡化計算(如下圖所示)。我們将地理空間劃分為M*N大小的網格(可以通過geohash對網格進行編碼,參考之前的博文《geohash》),是以max(P(m|p))就轉換為在地理空間找到一個網格,使得信号向量m出現的機率最大。
如何計算某網格p出現信号向量m的機率呢?
通過對“位置-信号”資料庫的清洗,可以統計每一個網格出現的信号向量的個數,即得到直方圖。
得到了網格p的信号向量直方圖後,我們就可以求P(m|p)的機率(p點所在的格子出現信号向量m的機率)。
然而實際上,對信号向量進行count幾乎不可能,盡管有很多請求百度定位的結果落在網格p内,但這些請求攜帶的信号向量幾乎不一樣,想得到有統計意義的直方圖幾乎不可能。
是以,我們繼續對公式進行簡化,我們假設各個wifi信号之間互相獨立,這個假設也是合理的。于是公式轉換為:
現在問題關鍵是求解P(wfi=RSSIi | p),即在網格p内,mac位址為wfi且信号強度為RSSIi出現的機率。我們可以事先統計一個網格p内每一個wifi信号的直方圖,這樣形成統計意義的直方圖較容易。
上述模型要求我們對地理空間進行網格化,并預先計算出每個網格内各個wifi對應的信号直方圖,并進行存儲。然而在實際應用我們網格數目将會非常多,存儲直方圖的開銷較大,是以要盡可能節省網格裡攜帶的資訊。是以一種思路是用高斯分布曲線模拟直方圖,這樣對于一個網格,隻需要存儲各個wifi對應的高斯分布的幾個參數即可。
當然,每個網格的直方圖曲線并不一定都能用高斯分布曲線來近似,一些文獻指出可能存在各種形态的曲線例如雙峰曲線等,是以也可以采用核密度估計的方法。
通過上述方法我們可以求出信号向量m出現最大可能性的網格,并取網格的中心點坐标傳回即可。當然有些時候很難判别,比如我們求得A和B兩個格子的機率幾乎相等,這個時候僅僅傳回A或者B就不太合适,權重插值是更為合理的選擇。一種比較魯棒的方法是我們找出topk個網格,然後進行插值。
3 問題及解決方法
1)離散網格大小如何确定?
如果網格過小,存儲量巨大,并且很多網格沒有任何信号直方圖;如果過大,精度得不到保證。一種方法網格大小為固定值,根據實驗結果來确定網格大小;更好的方法是自适應網格大小,對于信号較密急的地方(市區)網格設小,對于信号稀疏的地方(郊區)網格設大。
2)當使用者請求的信号向量裡存在一些新的mac位址對應的信号怎麼辦?
如果直接應用下述公式進行計算,那麼得到的機率将會是0,因為我們是機率連乘,隻要一項機率為0,整體結果就為0。為了去掉零機率,一個簡單的方法是采用加一平滑(add-one smoothing)或稱拉普拉斯平滑(Laplace smoothing)。
3)如何提高計算效率?
理論上使用者來一個請求,我們需要周遊計算資料庫每個網格對應的機率,并将最大機率網格對應的中心點傳回。假設我們格子是10*10米大小,那麼将北京全部網格化就有1.6億個格子,周遊計算開銷十分巨大。
一種提高計算效率的方法是首先根據使用者的信号向量求解出大緻空間範圍,然後計算該空間範圍的每一個格子的機率。
4 參考文獻
Practical Metropolitan-Scale Positioning for GSM Phones
CellSense: A Probabilistic RSSI-based GSM Positioning System
An Improved Algorithm to Generate a Wi-Fi Fingerprint Database for Indoor Positioning
Topical Issues: Location Fingerprinting
基于區間數聚類的無線傳感器網絡定位方法
基于一種優化的KNN算法在室内定位中的應用研究
轉載請标明源位址:http://www.cnblogs.com/LBSer