1.某公司要用鐵路運送2種物品,分别從城市s1、s2到d1、d2,每個物品每天要送出0.5機關。給出城市之間每天鐵路的流量限制。假設物品可以任意地分成若幹份,進而可以分别從不同的線路走。求一個開銷最小的運送方案。如圖:(ef之間出了故障。)
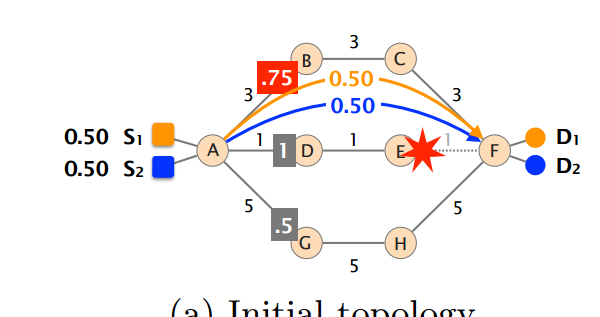
2個流s1--d1(設為流1)和s2--d2(設為流2),均隻有3條路可以走:a-b-c-f(設為路徑1),a-d-e-f(設為路徑2),a-g-h-f(設為路徑3)。設2個流在3條路徑上的流量分别為:x11,x12,x13,x21,x22,x23。
則目标函數:
min (9x11+9x21+10000x12+10000x22+15x13+15x23)
這裡因為df斷了,故令路徑2的開銷為10000,代表正無窮。
限制條件:
x11+x12+x13=0.5
x21+x22+x23=0.5
x11+x21<=0.75
x12+x22<=1
x13+x23<=0.5
解得x11=0.5,x21=x23=0.25,x12=x22=x13=0
LINDO求解如圖:
---------------------------------------------------------------------------------------------------------------------------------------------------------------------
《線性規劃的簡單應用和實作》這篇論文中描述的線性規劃解網絡流的限制條件:
其中4個條件可以分别了解為:
1.每條邊上的流量不能超過該邊的容量
2.除源點和彙點外的其他點,流入每點的流量和從該點流出的流量相等
3.從源點發出的某個流的量,以及流入彙點的某個流的量,等于該流需求發出的量
4.每條邊上的流是非負的
-----------------------------------------------------------------------------------------------------------------------------------------------
2.某公司要用鐵路運送3種物品,分别從城市s1、s2、s3到d1、d2、d3,每個物品每天分别要送出0.75、0.5、0.75機關。給出城市之間每天鐵路的流量限制。假設物品可以任意地分成若幹份,進而可以分别從不同的線路走。求一個開銷最小的運送方案。如圖:
将14條邊上的3種流分别設為x11,x12,……,x114,x21,x22,……,x214,x31,x32,……,x314如圖,依次類推。
則目标函數為:
min (3x12+3x22+3x32+x13+x23+x33+3x14+3x24+3x34+10x16+10x26+10x36+10x17+10x27+10x37+3x19+3x29+3x39+x110+x210+x310+3x111+3x211+3x311)
限制條件為:
x13+x23+x33<=1
x110+x210+x310<=1
x11=0.75
x21=0
x31=0
x18=0
x28=0.5
x38=0
x113=0
x213=0
x313=0.75
x15=0.75
x25=0
x35=0
x112=0
x212=0.5
x312=0
x114=0
x214=0
x314=0.75
x11-x12=0
x21-x22=0
x31-x32=0
x12+x16-x13=0
x22+x26-x23=0
x32+x36-x33=0
x13-x14-x17=0
x23-x24-x27=0
x33-x34-x37=0
x14-x15=0
x24-x25=0
x34-x35=0
x18+x113-x16-x19=0
x28+x213-x26-x29=0
x38+x313-x36-x39=0
x19-x110=0
x29-x210=0
x39-x310=0
x110-x111=0
x210-x211=0
x310-x311=0
x111+x17-x112-x114=0
x211+x27-x212-x214=0
x311+x37-x312-x314=0
----------------------------------------------------------------------------------------------------------------------------
3.需求:流從結點c傳輸到紅色結點,邊上沒有容量限制,求最小開銷的路徑。
如圖:
該圖為無向圖,将它轉化為有向圖,每條邊轉化為兩條反向的邊,如x1轉化為x11和x21,x2轉化為x12和x22……
目标函數:
min 10x11+10x21+15x12+15x22+5x13+5x23+10x14+10x24+30x15+30x25+50x16+50x26+10x17+10x27+100x18+100x28+25x19+25x29
x11+x22-x12-x21=1
x18-x28=1
x11+x23+x29-x21-x13-x19=0
x23+x24-x13-x14=0
x14+x12-x24-x22=0
x19+x25+x27-x29-x15-x17=0
x17+x28+x16-x27-x18-x26=0
得出CAFD的路徑。
----------------------------------------------------------------------------------------------------------------
4.若上圖要求從B傳到紅色結點。
目标函數不變,限制條件變為:
x11+x22-x12-x21=0
x23+x24-x13-x14=1
LINDO解出BAFD的路徑。