目錄
- 馬爾可夫理論
- 馬爾可夫性質
- 馬爾可夫過程(MP)
- 馬爾可夫獎勵過程(MRP)
- 值函數(value function)
- MRP求解
- 馬爾可夫決策過程(MDP)
- 效用函數
- 優化的值函數
- 貝爾曼等式
- 參考
DQN發展曆程(一)
DQN發展曆程(二)
DQN發展曆程(三)
DQN發展曆程(四)
DQN發展曆程(五)
- P[St+1 | St] = P[St+1 | S1,...,St]
- 給定目前狀态 St ,過去的狀态可以不用考慮
- 目前狀态 St 可以代表過去的所有狀态
- 給定目前狀态的條件下,未來的狀态和過去的狀态互相獨立。
- 形式化地描述了強化學習的環境。
- 包括二進制組(S,P)
- 根據給定的轉移機率矩陣P,從目前狀态St轉移到下一狀态St+1,
- 基于模型的(Model-based):事先給出了轉移機率矩陣P
- 和馬爾可夫過程相比,加入了獎勵r,加入了折扣因子gamma,gamma在0~1之間。
- 馬爾可夫獎勵過程是一個四元組⟨S, P, R, γ⟩
- 需要折扣因子的原因是
- 使未來累積獎勵在數學上易于計算
- 由于可能經過某些重複狀态,避免累積獎勵的計算成死循環
- 用于表示未來的不确定性
- gamma越大表示越看中未來的獎勵
- 引入了值函數(value function),給每一個狀态一個值V,以從目前狀态St到評估未來的目标G的累積折扣獎勵的大小
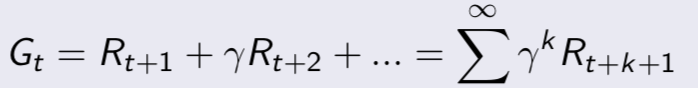
- v = R + γPv (矩陣形式)
- 直接解出上述方程時間複雜度O(n^3), 隻适用于一些小規模問題
- 加入了一個動作因素a,用于每個狀态的決策
- MDP是一個五元組⟨S, A, P, R, γ⟩
- 政策policy是從S到A的一個映射
- 相比于值函數,加入了一個動作因素
- 為了求最佳政策,在值函數求解時,選擇一個最大的v來更新目前狀态對應的v
- 和值函數的求解方法相比,不需要從目前狀态到目标求解,隻需要從目前狀态到下一狀态即可(根據遞推公式)
david siver 課程
https://home.cnblogs.com/u/pinard/