零.Github連結
https://github.com/xxr5566833/sudo
一.PSP表格
| PSP2.1 | Personal Software Process Stages | 預估耗時(分鐘) | 實際耗時(分鐘) |
|---|---|---|---|
| Planning | 計劃 | ||
| · Estimate | · 估計這個任務需要多少時間 | 10 | |
| Development | 開發 | ||
| · Analysis | · 需求分析 (包括學習新技術) | 120 | |
| · Design Spec | · 生成設計文檔 | 60 | |
| · Design Review | · 設計複審 (和同僚稽核設計文檔) | 30 | |
| · Coding Standard | · 代碼規範 (為目前的開發制定合适的規範) | ||
| · Design | · 具體設計 | ||
| · Coding | · 具體編碼 | 600 | |
| · Code Review | · 代碼複審 | 300 | |
| · Test | · 測試(自我測試,修改代碼,送出修改) | 200 | |
| Reporting | 報告 | ||
| · Test Report | · 測試報告 | ||
| · Size Measurement | · 計算工作量 | 10 | |
| · Postmortem & Process Improvement Plan | · 事後總結, 并提出過程改進計劃 | ||
| 合計 | 1540 |
二.解題思路描述
這道題一共有兩個部分,一部分是生成數獨終局,另一部分是解決給定數獨問題,兩者都要把最後的數獨結果輸出到檔案中。
1.數獨生成
數獨生成一開始就想到用遞歸回溯的方法搜尋所有的可行解,具體思路也不細說了,就是對每一個需要填的空搜尋可行解,之後的很長一段時間我都是在優化這個算法,但是速度還是一直很慢,是以後來又和同學讨論出了另外一個方法,就是使用數獨模闆和行列交換的方法産生數獨,速度提高了很多很多。下面分别描述這兩部分。
(1)遞歸方法生成數獨終局
這裡我沒有選用普通的從(0,0)開始一直搜尋到(8,8)。我的搜尋的過程是:按照确定好的填入數字的順序,對每個3*3的小九宮格的确定這個數字在這個小九宮格中的位置。這樣做相比于原來的一個空一個空的搜尋,我覺得好處是:通過自己确定填入小九宮格的順序和要填入的數字的順序,可以保證每次填入的位置所在的3*3的小九宮格一定沒有包含目前這個數字,這樣在判斷是否可以填入時,隻需要判斷目前行的列的情況就可以了。
但是遞歸算法速度還是很慢,即使我一直在優化,最後生成一百萬個數獨的時間還是很長。于是我通過和其他人讨論,也參考了大家在群裡的讨論,同時也參考了《程式設計之美》,确定了另一種數獨的生成算法。
(2)通過模闆和行列交換生成數獨終局
這個方法可以分為兩個部分:
①通過第一行數字和模闆,産生一個原始的數獨矩陣;
②通過對這個數獨矩陣的行和列進行局部交換,産生符合數獨要求的不同數獨矩陣。
下面就分這兩部分叙述。
産生原始數獨矩陣:
| a | b | c | d | e | f | g | h | i |
這是一個模闆,其中的a~i分别表示一個數字。如果我能确定好第一行,那麼通過這個模闆映射關系,我們就可以由第一行生成2~9行。具體的映射關系可以這樣描述:假如第一行是(9,8,7,6,5,4,3,2,1),那麼數字9就對應了上面模闆的字母a,然後我們通過這個模闆可以确定字母a在第二行的第7個格子裡(從1開始算起),是以我們就能确定第二行的數字9的位置是在第6個格子。之後的每個數字同理,确定了第二行的數字後,繼而可以确認第三行,第四行...最後就可以得到原始的數獨矩陣。
可以看出原始矩陣的生成是通過第一行的排列情況和模闆确定的,其中模闆是确定不變的,而我們可以通過改變第一行的排列情況來産生不同的原始矩陣。具體的第一行的情況總數就是8個數字的全排列數量(第一個數字是确定的,是以隻需要排列其他的數字)。
這樣可以生成8!=40320種不同的原始數獨矩陣,還不夠題目中的最大數量要求。我們還需要通過行列變換來産生不同的數獨矩陣。
行列變換:
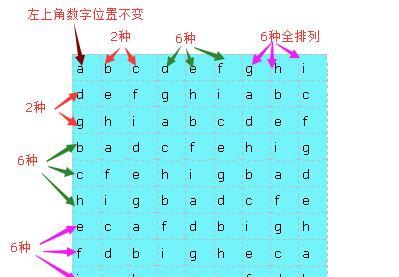
對于通過模闆和第一行生成的原始數獨矩陣,我們可以通過局部的行列變換來生成更多的矩陣。我的變換方法是:
①左上角這個數字的位置不能變,每次交換是交換整個一行或者整個一列;
②把9行分為三個大行,第一個大行包括第2行和第3行,這時可以選擇交換第2行和第3行,是以第一個大行有2種情況。第二個大行包括第4,5,6行,此時這三行的每一種全排列 交換情況都可以,比如我可以通過交換讓第二個大行變成(4,6,5),是以第二個大行有6種,同理第三個大行也有6種。
③這9列也同理,分為三個大列,和行一樣,分别有2種,6種和6種排列情況。
④不同的交換情況是互相獨立的!即某一部分行列的交換不會影響其他的行和列的交換情況數量的增減,是以根據排列組合知識,我們可以得到總的情況數是每一種行列變換情 況數的乘積。
是以我們可以得到,對于每一個原始矩陣,我們可以産生2*2*6*6*6*6種數獨矩陣,而原始數獨矩陣的産生,即之前說的第一個過程和這裡的行列交換是互相獨立的,是以一共的情況數是8!*4*6*6*6*6,已經可以達到題目的要求了。
模闆加行列變換生成數獨算法的思考:
這樣做确實生成速度快,但是我們還是需要審視這個算法,它到底滿不滿足兩個條件:
①生成的數獨矩陣都是合法的嗎?
②生成的數獨矩陣都是不重複的嗎?
下面我們從這兩個部分證明一下:
首先需要确定生成的數獨矩陣都合法嗎?合法的數獨需要滿足3個條件:
①每一行1-9這九個數字有且僅有一個
②每一列1-9這九個數字有且僅有一個
③每個3*3的九宮格中1-9這九個數字有且僅有一個
審視我們之前的這個算法,假設變換前是合法的數獨,先看行變換:
①先看行變換後是否符合數獨合法性。因為每個行變換都是在整個行的基礎上變換,因為原來這個行就滿足條件,是以變換後肯定也滿足行的條件。
②因為每個行變換,僅僅影響每個數字在所在列的位置,但是仍然滿足每個列每個數字僅僅出現一次,是以行變換後也滿足列的條件
③因為每個行變換都是在一個大行的範圍内排列的,一個大行就是之前說的把1-9行分為1-3,4-6,7-9這三個大行,是以在大行内無論怎麼交換,僅僅改變每個數字在其九宮格内 内的位置,并不影響原來就滿足的九宮格條件。
是以綜上,一個合法數獨經過行變換并不會違反數獨的條件,同理,列變換也不會違反數獨的條件。而行變換和列變換之間是互相獨立的,是以綜上,行變換,列變換和行列變換的組合都不會違反數獨的條件。
然後要确定這樣産生的數獨矩陣不會重複。兩個數獨矩陣重複意味着這兩個數獨矩陣每個位置上的數字都相等。關于不會重複的證明,不如就按照之前說的兩步操作①産生原始數獨矩陣②行列變換來證明。
很容易就可以得到的是:對于一個原始數獨矩陣,對它進行不同的行列變換,得到的數獨矩陣是不同的。
我們不妨把數獨的生成過程倒過來,我們先通過對模闆進行行列變換,那麼對于不同的行列變換,我們一定可以得到不同的模闆矩陣。例如下圖就是上面那個模闆矩陣交換了第二列和第三列後生成新的模闆。
然後我們建立a~i和1~9的一 一映射關系,這樣的映射關系考慮到第一個數字是固定的,那麼一共有8!種不同的映射關系。
而對于一個模闆矩陣來說,不同的映射關系,一定會産生不同的數獨矩陣。
前面的其實都很好了解,即很容易知道①對于原始的模闆,不同的行列變換,最後産生的模闆矩陣不一樣②對于一個産生的模闆矩陣,不同的映射關系,産生的數獨也不一樣。那麼對于不同的模闆矩陣,不同的映射關系得到的數獨矩陣一定不同嗎?這個問題我一開始是不确定的,我懷疑可能會有某種模闆和某種映射的組合會與另外一種模闆和另外一種映射的組合最後産生的數獨矩陣是一樣的。
在通過舉了一些例子後,我發現原來預想的重複情況沒有發生,但是嚴謹的證明我現在還沒有完整的推導出來...等我想清楚了再補充吧。
是以這個生成算法的不重複性目前我還不太能保證...
2.數獨求解
我所使用數獨的求解算法就是遞歸的搜尋算法。通過搜尋每一個空的可行解來完成整個數獨。
但是一開始這樣很慢,于是我便加入了預處理的過程,即一開始多次周遊整個數獨,把那些可能的取值隻有一個的空先填上,然後再遞歸回溯。
但是這樣改進對于很多一開始找不到某個空有唯一解的數獨來說是沒有用的,整個算法還是很慢,之後我便用了VS帶的性能分析工具,發現整個搜尋過程耗費時間最多是我的判斷是否可以填入的函數。我一開始的判斷是否可以填入的函數是通過周遊這個空所在的行,列,3*3九宮格來确定是否可以填入的,經過思考後作出了改進:我通過建立三個數組,分别記錄某一行/某一列/某個九宮格 這個數字是否可以填入。在進行填入/清除操作時,更新這三個數組,在判斷是否可以填入時,直接根據這三個數組來判斷,這樣增加了一點空間消耗,但是減少了很多時間花費。
三.設計實作過程
1.代碼組織
這裡我設計了兩個類,一個是數獨的生成類,另一個是數獨的求解類,這兩個類是互相獨立的,分别用于數獨的求解和生成。
一開始接觸C++,很多特性還不會運用,而且因為之前優化速度花了很大的時間,導緻沒有太多時間提升代碼的維護性和擴充性,同時代碼中函數之間的耦合性還是很大,因為沒時間修改了,怕修改會影響正确性,是以這裡把問題列舉一下,以後修改:
(1)數獨生成過程耦合性大。我的數獨生成過程是這樣的:
但是第一行的全排列的生成函數目前和原始數獨的生成函數耦合在一起,即每生成一個新的全排列就會直接調用原始數獨的生成函數:
好的解決辦法應該是,把每個生成的全排列記錄下來,然後在生成原始矩陣時取出來用就好。
(2)空間開銷過大。在實作時我進行了很多次的數獨矩陣的儲存操作,比如從檔案中讀入一個待求解矩陣後,我還把它copy到數獨解決類的一個成員變量裡。其實很多時候是不需要儲存的,但是因為自己的指針還有記憶體的基礎知識欠缺吧,總是想着進行備援的複制操作以保證結果的正确性。現在我對這方面的改進做出如下計劃:
①對于數獨的生成,一開始為了追求效率,把所有的矩陣都生成好以後,把它們整個放入一個字元串緩存中一次寫入檔案。雖然這樣加快了速度,但是完全可以每一次生成好一個矩陣後就進行寫入操作,這樣空間開銷大大降低。數獨的解決同理
②很多地方的數獨的copy都是沒有必要的,有兩處:一是從檔案中讀入數獨矩陣時,完全可以直接讀到數獨解決類的成員變量中,而我卻先把它讀到一個二維數組,然後在生成數獨解決對象時又把這個二維數組中的值複制到對象的成員變量中;
(3)類中成員函數和成員變量還有備援,其中C++的先聲明再定義的特性還是優點不太适應。
2.單元測試的設計
對于單元測試目前我設計了關于下面這些功能的檢測:
(1)測試了數獨的生成算法是否可以生成不重複的數獨。這裡使用了字典樹的方法。
(2)測試了數獨解決算法中用到的輔助函數,包括①判斷是否可以被填入②填入函數③清除函數。
四.改程序式性能
我在提高程式的速度上花了很多的功夫,以至于現在的程式空間消耗過大了...
1.提高生成數獨的速度
生成數獨整個過程其實可以分成兩個部分:生成100萬個數獨,把這100萬個數獨存入檔案。
生成100萬個數獨我用過兩種方法:①遞歸回溯②模闆加行列交換
寫入檔案我用了三種方法:①每生成一個數獨,就寫入檔案中,而且寫入是每次都調用fprintf寫入一個字元或者一個數字②先把每次要寫入的數獨矩陣存在一個字元串緩存中,然後一次用fprintf存入③把整個100萬個矩陣存在一個字元串中,最後用fprintf一次寫入④改用fstream寫入檔案。
一開始我是用遞歸回溯方法生成數獨,而且每次生成一個矩陣就一個字元一個數字的寫入到檔案中。當然這樣做特别慢,即使我優化了遞歸回溯的過程,生成整個100萬個數獨矩陣并寫入還是需要花費2分鐘左右
然後我通過VS的性能探測工具,發現了原來花費時間最多的是IO:
(可以看到fprintf占CPU時間比重大)
然後我就看到大家在群裡的讨論,自己也和同學進行了讨論,把寫入過程修改為把整個數獨矩陣放在一個字元串中,然後調用fprintf寫入,這樣一改,果然快多了!現在整個時間開銷僅僅需要17s左右。其中IO大概花費11s左右
(使用遞歸回溯算法+把數獨矩陣放入字元串中用fprintf寫入)
(把整個數獨矩陣放入字元串中寫入 100萬個需要的花費時間)
然後我嘗試把100萬個矩陣放在一個字元串中,在生成完後一次寫入...IO時間的花費更少了,需要9s
(把100萬個數獨矩陣放在一個字元串中調用fprintf一次寫入)
最後我聽取了别人的意見,轉而使用fstream把100萬個數獨矩陣一次性寫入檔案中,最後的時間花費更少了,僅僅需要4s
上面都是對IO的優化,下面講對數獨生成算法的優化。數獨生成算法一開始我用的是遞歸回溯算法,即使優化了很多,但是速度還是很慢。于是我就選擇之前說的模闆+等價交換的方法,産生的數獨速度大大提高了。現在僅僅需要2s内就可以生成100萬個數獨終局(不包含檔案寫入)
現在整個過程所需要的時間可以達到4s
然後還可以通過開編譯優化,進一步提高速度。
生成可以達到1s以内,寫入可以在3s,感覺編譯優化後對IO性能提升不算很大?但是生成速度提高了很多。
2.提高解決數獨的速度
我選擇的解決數獨的算法就是遞歸回溯,我也沒有具體的優化太多數獨的解決算法,時間都用在優化數獨生成了...是以這裡我所做的優化就是加了一個預處理的過程,這個預處理過程其實就是先周遊整個數獨的未填的空,如果能找到某個空隻有一種選擇,那麼就可以直接填進去了。然後繼續周遊整個數獨矩陣直到整個數獨矩陣沒有可以直接填入的空格,然後開始進行遞歸回溯。
其實這個預處理對于簡單的數獨可能會提高速度,但是如果這個沒有這樣的隻有一個選擇的空格可以填,那麼這個預處理過程其實是無用的。
之後要研究一下用DLX解決數獨問題。
五.代碼說明
核心代碼有兩部分,一部分是數獨的生成算法,另一部分是數獨的解決算法。
(1)數獨的生成算法:
1 void sudoCreate::getMatrix(int array[8])
2 {
3 this->matrix[0][0] = 3; //(0,0)上數字固定為3
4 for (int i = 1; i < 9; i++) {
5 this->matrix[0][i] = array[i - 1];
6 }
7 /*根據map的關系和第一行的某個排列生成其他行*/
8 for (int i = 1; i < 9; i++) {
9 for (int j = 0; j < 9; j++) {
10 this->matrix[i][j] = this->matrix[0][map[i * 9 + j]-1];
11 }
12 }
13 /*使用多層for循環産生行和列不同交換情況的組合
14 具體是這樣的:(從第0列開始)
15 第一層循環是用于是否交換第1列和第2列
16 第二層循環是用于第3,4,5列的不同排列情況,從(3,4,5)産生全排列序列可以這麼交換:
17 (3,4,5)交換(1,2)列得到(3,5,4)
18 (3,5,4)交換(0,1)列得到(5,3,4)
19 (5,3,4)交換(1,2)列得到(5,4,3)
20 (5,4,3)交換(0,1)列得到(4,5,3)
21 (4,5,3)交換(1,2)列得到(4,3,5)
22 (4,3,5)交換(0,1)列得到(3,4,5)
23 可以生成整個全排列并恢複為原來的狀态
24 這也是下面的switch語句的含義
25 之後幾層循環同理
26 */
27 for (int i1 = 0; i1 < 2; i1++) {
28 switch (i1) {
29 case 0:
30 case 1:
31 for (int j = 0; j < 9; j++) {
32 this->swap(&(matrix[j][1]),&(matrix[j][2]));
33 }
34 break;
35 default:
36 break;
37 }
38 for (int i2 = 0; i2 < 6; i2++) {
39 switch (i2) {
40 case 1:
41 case 3:
42 case 5:
43 for (int j = 0; j < 9; j++) {
44 this->swap(&(matrix[j][3]),&(matrix[j][4]));
45 }
46 break;
47 case 0:
48 case 2:
49 case 4:
50 for (int j = 0; j < 9; j++) {
51 this->swap(&(matrix[j][4]),&(matrix[j][5]));
52 }
53 break;
54 default:
55 break;
56 }
57 for (int i3 = 0; i3 < 6; i3++) {
58 switch (i3) {
59 case 1:
60 case 3:
61 case 5:
62 for (int j = 0; j < 9; j++) {
63 this->swap(&(matrix[j][6]), &(matrix[j][7]));
64 }
65 break;
66 case 0:
67 case 2:
68 case 4:
69 for (int j = 0; j < 9; j++) {
70 this->swap(&(matrix[j][7]), &(matrix[j][8]));
71 }
72 break;
73
74 default:
75 break;
76 }
77 for (int i4 = 0; i4 < 2; i4++) {
78 switch (i4) {
79 case 0:
80 case 1:
81 for (int j = 0; j < 9; j++) {
82 this->swap(&(matrix[1][j]), &(matrix[2][j]));
83 }
84 break;
85 default:
86 break;
87 }
88 for (int i5 = 0; i5 < 6; i5++) {
89 switch (i5) {
90 case 1:
91 case 3:
92 case 5:
93 for (int j = 0; j < 9; j++) {
94 this->swap(&(matrix[3][j]), &(matrix[4][j]));
95 }
96 break;
97 case 0:
98 case 2:
99 case 4:
100 for (int j = 0; j < 9; j++) {
101 this->swap(&(matrix[4][j]), &(matrix[5][j]));
102 }
103 break;
104
105 default:
106 break;
107 }
108 /*将産生的矩陣存好*/
109 int* newmatrix = (int *)malloc(81*sizeof(int));
110 for (int i = 0; i < 9; i++)
111 for (int j = 0; j < 9; j++)
112 newmatrix[i*9+j] = this->matrix[i][j];
113 matrixarray[count] =newmatrix;
114 this->count++;
115
116 if (this->count == this->num) {
117 return ;
118 }
119
120 }
121 }
122 }
123 }
124 }
125 return ;
126 } 這裡需要注意的是,用for循環來實作某幾行或者幾列的全排列時,需要注意交換的順序。這裡我一開始想錯了,因為我一開始是通過for循環的循環變量來決定目前該如何交換,比如我可以設定(1,2,3)的全排列和數字0-5這樣的映射關系:0 對應 (1,2,3) 1 對應 (1,3,2) 2對應(2,1,3)等等以此類推,是以我可以根據目前的for循環的變量是多少,來決定如何交換。
但是我們是直接在這個數獨矩陣上進行交換的,是以在進行下一次交換時,使用的數獨矩陣是上一次交換過的,是以不能錯誤的認為交換都發生在原始的矩陣上。
(2)數獨的解決算法
void sudoSolver:: solve(int arrayindex) {
if (this->solved == true)
return;
if (arrayindex > maxempty - 1) {
this->solved = true;
int* newmatrix = (int *)malloc(81 * sizeof(int));
for (int i = 0; i < 9; i++)
for (int j = 0; j < 9; j++)
newmatrix[i * 9 + j] = this->matrix[i][j];
this->matrixarray[count] = newmatrix;
count++;
return;
}
int i = rchoice[arrayindex];
int j = cchoice[arrayindex];
// print(this->matrix);
for (int k = 1; k <= 9; k++) {
if (canFill(i, j, k)) {
this->fillin(i, j, k);
solve(arrayindex + 1);
this->erase(i, j, k);
}
}
} 就是很簡單的遞歸回溯搜尋,這裡就不再贅述了。
六.PSP表格展示
| 600 | 800 | ||
| 400 | |||
| 1780 |
七.總結
第一次作業很多地方我都沒有實作的很好,在截止時間之前,很多地方還沒有完成:
(1)代碼的不同功能之間的耦合性還是很高,代碼還有很多備援的地方,C++的基礎知識感覺需要補充補充;
(2)空間消耗過大,可以再減少空間消耗的;
(3)建構之法草草的浏覽了一遍,還沒有自己的思考。
(4)覺得自己在一開始的設計那裡還需要加強,因為經常出現編碼中途改變之前的預定設計,導緻整個流程在具體編碼那一步就停止不前...
不過經過這一周的編碼,我學到了很多知識:
(1)學會了基本的優化程式的方法,包括使用更快的算法,盡量減少IO讀寫的次數
(2)學會了系統的個人軟體開發的流程,雖然現在實際實施的并不太好,但是我會努力嚴格按照PSP表格上的流程完成個人開發的
還有很多很多其他的開發知識,雖然這個第一次作業花了很長的時間,其實體驗并不太好,但是我相信自己會越來越适應這個課的節奏的,相信自己會學到越來越多的實際開發知識。