天天看點
傳回

[2017北航軟工]第1次個人項目——求解數獨與生成數獨終局

[2017北航軟工]第1次個人項目

——求解數獨與生成數獨終局

項目GitHub位址 https://github.com/Hesitater/Sudoku

解題思路

這次的數獨問題主要可分為求解數獨與生成終局兩大部分。最開始拿到題目的時候，我決定先完成生成終局，再求解數獨，然而找到的大部分生成數獨的算法都無法滿足生成1000000個不同終局的要求。雖然初始決策的錯誤讓我繞了一些彎路，但也讓我拜識不同生成終局的算法，在這裡将找到的終局生成算法貼出來：

  • Swing數獨遊戲(一)：終盤生成之矩陣轉換法
  • Java code to generate sudoku puzzle
  • 數獨-- 一個高效率生成數獨的算法

前兩個算法用的都是對已有終局進行行、列、單元格交換的生成方法，最後一個算法比較有特色，雖然也需要終局，但相較前兩者加入了一定随機性。

求解數獨

在發現先生成終局這條路走不通後，我改變了政策，選擇先完成求解數獨的功能。在谷歌求解算法的過程中，翻到了Ladit同學的這篇部落格：深度優先搜尋和回溯法生成數獨。我最後采用了部落格中推薦的DLX算法來求解數獨。由于使用指針操作以及算法解法的巧妙，DLX算法算是數獨求解算法當中效率較高的，以下是對DLX算法講解得比較全面而又易懂的兩篇部落格：

  • 用DLX解sudoku(數獨)
  • 解數獨——dancing link X

生成終局

生成終局同樣利用求解數獨的DLX算法就能完成。如果将DLX算法看做一個函數，求解數獨的過程就是把挖了空的終局作為參數傳給函數，讓函數把空位填滿；生成終局的過程就是把沒有數字的空數獨(除了第一個格子被填上指定數字)作為參數傳給函數，讓函數把空位填滿。

這篇部落格也提供了一個DLX和深度優先搜尋結合的方式生成數獨。這個算法給數獨生成增加了一定随機性而又能保證生成的終局數量，值得參考——産生數獨謎題

整體設計

類結構：

一共有8各類，可分為兩大部分:

  • DLX：
      1. DLXNode——DLX節點類
      1. ColumnHead——DLXNode子類，列頭類
      1. CommonNode——DLXNode子類，普通節點類
      1. DLXGenerator——DLX十字連結清單建立類
      1. DLXSolver——DLX問題求解類
  • Sudoku:
      1. SudokuLoader——檔案存取操作類
      1. SudokuSolver——數獨求解類，以DLXSolver為核心
      1. SudokuGenerator——終局生成類

代碼組織：

數獨的求解與終局生成都是建立在DLX算法的基礎上的，是以為DLX算法單獨設立了5個類來管理DLX算法，明确各部分分工。

單元測試：

貼出程式的兩個重要方法的測試

SudokuSolver::solveSudoku

：測試解出的數獨是否與答案相符

TEST_METHOD(TestSolveSudoku) {
    vector<int> puzzleVector;
    vector<int> solutionVector;
    int puzzle[81] = {
        0,1,2,3,4,0,7,8,9,
                7,8,9,5,1,2,3,4,6,
                3,4,6,7,8,9,5,1,2,
                2,5,1,0,3,4,9,6,7,
                6,9,7,2,5,1,8,3,4,
                8,3,4,6,9,7,2,5,0,
                1,2,5,4,7,3,6,9,8,
                9,6,8,0,2,5,4,7,3,
                4,7,3,9,6,8,1,2,0 };
    vector solution[81] = {
        5,1,2,3,4,6,7,8,9,
                7,8,9,5,1,2,3,4,6,
                3,4,6,7,8,9,5,1,2,
                2,5,1,8,3,4,9,6,7,
                6,9,7,2,5,1,8,3,4,
                8,3,4,6,9,7,2,5,1,
                1,2,5,4,7,3,6,9,8,
                9,6,8,1,2,5,4,7,3,
                4,7,3,9,6,8,1,2,5
    };
    for (int i = 0; i < 81; i++) {
        puzzleVector.push_back(puzzle[i]);
    }
    SudokuSolver solver;
    DLXNode* listHead = new DLXNode();
    solver.solveSudoku(listHead, puzzleVector, solutionVector);
    for (int j = 0; j < 81; ++j) {
        Assert::AreEqual(solutionVector[i], solution[i]);
    }
}

SudokuGenerator::generate

: 測試生成的數獨是否滿足數獨的限制與格式

TEST_METHOD(TestGenerateSudokus) {
        SudokuSolver solver;
        DLXNode* listHead = new DLXNode();
        vector<vector<int>> sudokus;
        vector<int> answers;
        SudokuGenerator generator;
        generator.generateSudokus(10);
        for (int i = 0; i < 10; ++i) {
            Assert::AreEqual(solver.solveSudoku(listHead, sudokus[i], answers),true);
        }
}

性能分析

[2017北航軟工]第1次個人項目——求解數獨與生成數獨終局

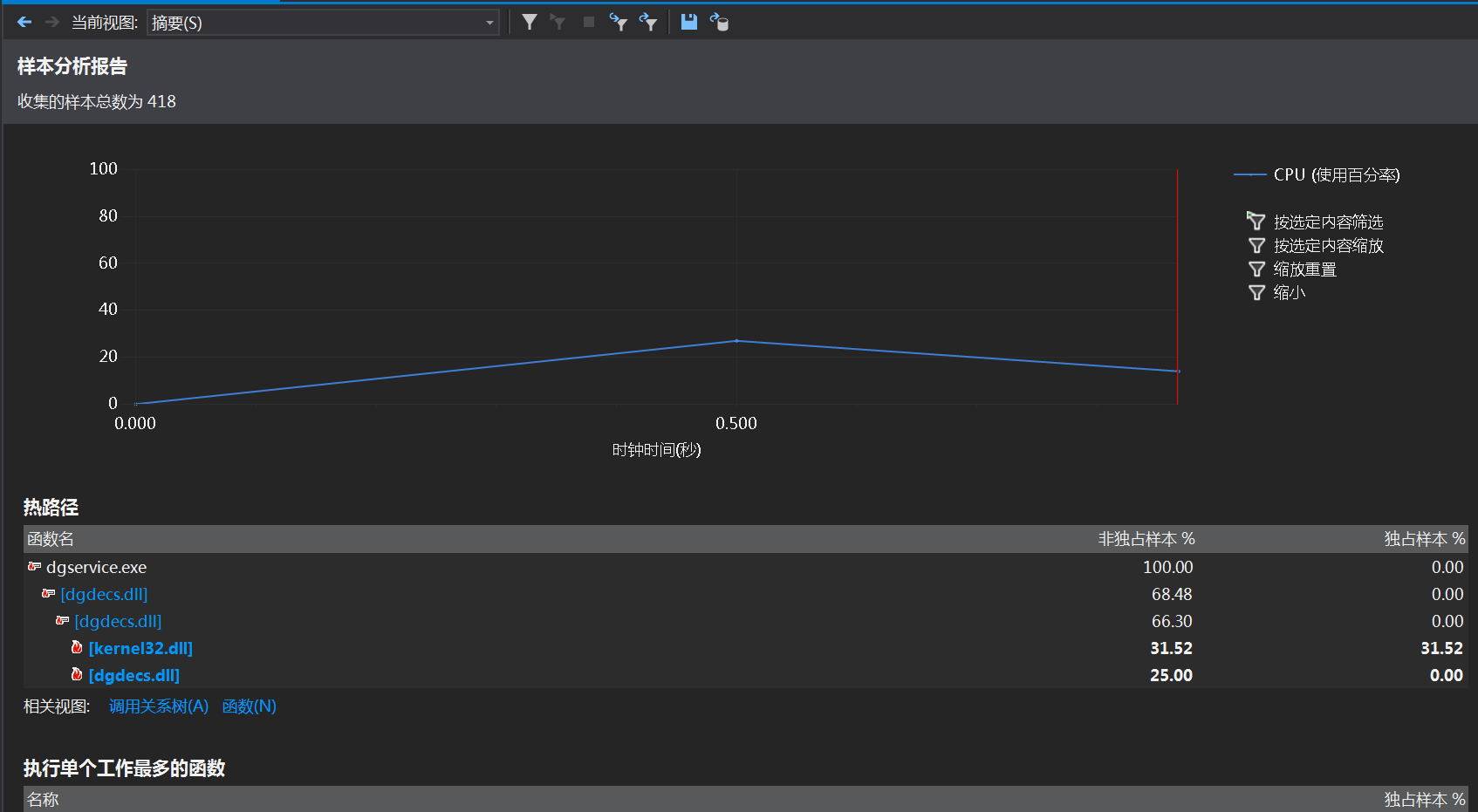
上圖為VS生成的本次項目的樣本分析報告

[2017北航軟工]第1次個人項目——求解數獨與生成數獨終局

從上面的調用樹可以看出，整個程式占用資源最多的方法是SudokuSolver::solveWithMultiAnswers，這個方法主要負責利用DLX算法完成求解工作，暫時未想到性能改進的辦法。

代碼說明

DLX部分：

  • DLXGenerator::appendLine

     :增加一行元素到DLX十字連結清單底部 
void DLXGenerator::appendLine(vector<ColumnHead*> columnHeads, vector<int> elementSubscripts, int rowIndex){
    CommonNode* lastHorizontalNode = NULL;
    CommonNode* firstHorizontalNode = NULL;

    for (int i = 0; i < elementSubscripts.size(); ++i) {
        int subscript = elementSubscripts[i];
        ColumnHead* columnHead = columnHeads[subscript];
        CommonNode* currentNode = new CommonNode(rowIndex, columnHead);
        DLXNode *lastVerticalNode = columnHead->upNode;

        //Link vertical nodes
        lastVerticalNode->appendDownNode(currentNode);
        currentNode->appendDownNode(columnHead);

        //Link horizontal nodes
        if (i == 0) {
            firstHorizontalNode = currentNode;
            lastHorizontalNode = currentNode;
        } else {
            lastHorizontalNode->appendRightNode(currentNode);
            lastHorizontalNode = currentNode;
        }

        currentNode->columnIndex = columnHead->columnIndex;
        columnHead->numberOfOne++;
    }

    lastHorizontalNode->appendRightNode(firstHorizontalNode);
}

  • DLXSolver::solveWithOneAnswer

     :求解DLX十字鍊（隻求一個解），參數listHead為DLX十字鍊鍊頭，solution中存儲所有解的行号。 
bool DLXSolver::solveWithOneAnswer(DLXNode *listHead, vector<int>& solution, int depth) {
    if (listHead->rightNode == listHead) { //Solution found
        /*for (int i = 0; i < depth; ++i) { //Debugging code
            cout << solution[i] <<endl;
        }*/
        return true;
    }

    //Select column with least one's
    ColumnHead* columnHead = selectColumn(listHead);
    cover(columnHead);

    bool solutionFound = false; //Usage: return type

    //Loop rows with one in column below columnHead
    for (DLXNode* node = columnHead->downNode; node != columnHead; node = node->downNode) {
        solution.push_back(((CommonNode*)node)->rowIndex); //Add temporary tempSolution node

        for (DLXNode* node2 = node->rightNode; node2 != node; node2 = node2->rightNode) {
            cover(((CommonNode*)node2)->columnHead);
        }

        depth++;
        solutionFound = solveWithOneAnswer(listHead, solution, depth); //Enter next recursion level
        depth--;

        for (DLXNode* node2 = node->leftNode; node2 != node; node2 = node2->leftNode) {
            uncover(((CommonNode*)node2)->columnHead);
        }

        if (solutionFound){ //Solution found, jump out loop
            break;
        }

        solution.pop_back(); //Delete temporary tempSolution node
    }
    uncover(columnHead);

    return solutionFound;
}

  • DLXSolver:: solveWithCertainAnswers

     :對一個DLX十字連結清單，求多(answerCount)個解 
void DLXSolver:: solveWithCertainAnswers(DLXNode *listHead, vector<int>& tempSolution, vector<vector<int>>& lastSolution,
                                         int answerCount, int depth) {
    if (listHead->rightNode == listHead) { //One solution found
        /*for (int i = 0; i < depth; ++i) { //Debugging code
            cout << tempSolution[i] <<endl;
        }*/
        lastSolution.push_back(tempSolution);
        return;
    }

    ColumnHead* columnHead = selectColumn(listHead);
    cover(columnHead);

    for (DLXNode* node = columnHead->downNode; node != columnHead; node = node->downNode) {
        tempSolution.push_back(((CommonNode*)node)->rowIndex); //Add temporary tempSolution node

        for (DLXNode* node2 = node->rightNode; node2 != node; node2 = node2->rightNode) {
            cover(((CommonNode*)node2)->columnHead);
        }

        depth++;
        solveWithCertainAnswers(listHead, tempSolution, lastSolution, answerCount, depth); //Enter next recursion level
        depth--;

        for (DLXNode* node2 = node->leftNode; node2 != node; node2 = node2->leftNode) {
            uncover(((CommonNode*)node2)->columnHead);
        }

        if (lastSolution.size() == answerCount) { //Solution count achieved get out of recursion
            break;
        }

        tempSolution.pop_back(); //Delete temporary tempSolution node
    }
    uncover(columnHead);
    return;
}

Sudoku部分：

  • SudokuSolver::solveSudoku

     :得到所給數獨題的一個解，傳到answer中 
void SudokuSolver::solveSudoku(DLXNode *listHead, vector<int> &sudoku, vector<int> &answer) {
    transformToList(sudoku, listHead);
    DLXSolver dlxSolver = DLXSolver();
    vector<int> solution;
    dlxSolver.solveWithOneAnswer(listHead, solution, 0); //Got DLX answer

    solutionToAnswer(solution, answer); //Answer got
}

  • SudokuSolver::solveWithMultiAnswers

     :對一個數獨題求多(

    answercount

     )個解 
* void SudokuSolver::solveWithMultiAnswers(DLXNode *listHead, vector<int>& sudoku, vector<vector<int>>& answers, int answerCount) {
    transformToList(sudoku, listHead);
    DLXSolver dlxSolver = DLXSolver();
    vector<int> tempSolution;
    vector<vector<int>> lastSolution;
    dlxSolver.solveWithCertainAnswers(listHead, tempSolution, lastSolution, answerCount, 0); //Got DLX answer

    //Get answers from lastSolution
    for (int i = 0; i < answerCount; ++i) {
        vector<int> answer;
        solutionToAnswer(lastSolution[i], answer);
        answers.push_back(answer);
    }
}

  • SudokuGenerator:: generateSudokus

     :建立

    sudokuCount

     個不重複的終局 
vector<vector<int>> SudokuGenerator:: generateSudokus(int sudokuCount) {
    vector<vector<int>> answers;

    //Create an sudoku with all zero
    vector<int> originalSudoku;
    for (int j = 0; j < sudokuSize; ++j) {
        if (j == 0) { //The first one must be 5
            originalSudoku.push_back(5);
        }else {
            originalSudoku.push_back(0);
        }
    }

    //Solve the zero sudoku to get sudoku outcomes
    DLXGenerator generator = DLXGenerator();
    DLXNode* listHead = new DLXNode();
    SudokuSolver solver = SudokuSolver();
    solver.solveWithMultiAnswers(listHead, originalSudoku, answers, sudokuCount);
    return answers;
}

PSP表格

PSP2.1 Personal Software Process Stages 預估耗時（分鐘） 實際耗時（分鐘）
Planning 計劃 5 7
· Estimate · 估計這個任務需要多少時間
Development 開發 430 1020
· Analysis · 需求分析 (包括學習新技術) 120 600
· Design Spec · 生成設計文檔 30
· Design Review · 設計複審 (和同僚稽核設計文檔)
· Coding Standard · 代碼規範 (為目前的開發制定合适的規範) 10
· Design · 具體設計 20
· Coding · 具體編碼
· Code Review · 代碼複審
· Test · 測試（自我測試，修改代碼，送出修改） 180
Reporting 報告 70 160
· Test Report · 測試報告
· Size Measurement · 計算工作量
· Postmortem & Process Improvement Plan · 事後總結, 并提出過程改進計劃 125
合計 505 1207

小結

萬事開頭難。由于對文法、算法和各種工具的生疏，這次的項目花了不少時間，Deadline前才勉強把作業的基本要求達成。這一周的練習算是讓我頭次真正體會到高效學習的重要性，打算在下次項目嘗試指定階段性目标，可把一周的項目周期切割成三份，每個項目制定周期定為2~4天，希望能對效率提高有所幫助。

上一篇: [2017BUAA軟工]第0次個人作業
下一篇: 個人項目-數獨