要點
希爾(Shell)排序又稱為縮小增量排序,它是一種插入排序。它是直接插入排序算法的一種威力加強版。
該方法因DL.Shell于1959年提出而得名。
希爾排序的基本思想是:
把記錄按步長 gap 分組,對每組記錄采用直接插入排序方法進行排序。
随着步長逐漸減小,所分成的組包含的記錄越來越多,當步長的值減小到 1 時,整個資料合成為一組,構成一組有序記錄,則完成排序。
我們來通過示範圖,更深入的了解一下這個過程。
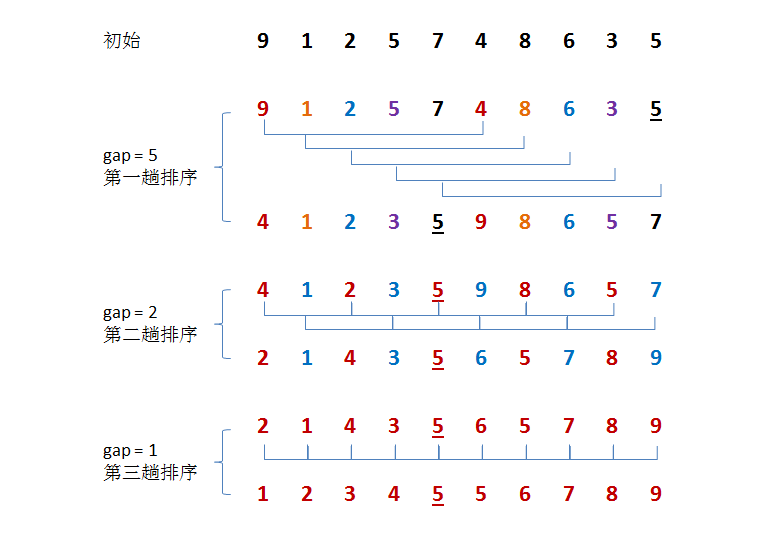
在上面這幅圖中:
初始時,有一個大小為 10 的無序序列。
在第一趟排序中,我們不妨設 gap1 = N / 2 = 5,即相隔距離為 5 的元素組成一組,可以分為 5 組。
接下來,按照直接插入排序的方法對每個組進行排序。
在第二趟排序中,我們把上次的 gap 縮小一半,即 gap2 = gap1 / 2 = 2 (取整數)。這樣每相隔距離為 2 的元素組成一組,可以分為 2 組。
按照直接插入排序的方法對每個組進行排序。
在第三趟排序中,再次把 gap 縮小一半,即gap3 = gap2 / 2 = 1。 這樣相隔距離為 1 的元素組成一組,即隻有一組。
按照直接插入排序的方法對每個組進行排序。此時,排序已經結束。
需要注意一下的是,圖中有兩個相等數值的元素 5 和 5 。我們可以清楚的看到,在排序過程中,兩個元素位置交換了。
是以,希爾排序是不穩定的算法。
核心代碼
public void shellSort(int[] list) {
int gap = list.length / 2;
while (1 <= gap) {
// 把距離為 gap 的元素編為一個組,掃描所有組
for (int i = gap; i < list.length; i++) {
int j = 0;
int temp = list[i];
// 對距離為 gap 的元素組進行排序
for (j = i - gap; j >= 0 && temp < list[j]; j = j - gap) {
list[j + gap] = list[j];
}
list[j + gap] = temp;
}
System.out.format("gap = %d:\t", gap);
printAll(list);
gap = gap / 2; // 減小增量
}
}
算法分析
希爾排序的算法性能
| 排序類别 | 排序方法 | 時間複雜度 | 空間複雜度 | 穩定性 | 複雜性 | ||
| 平均情況 | 最壞情況 | 最好情況 | |||||
| 插入排序 | 希爾排序 | O(Nlog2N) | O(N1.5) | O(1) | 不穩定 | 較複雜 |
步長的選擇是希爾排序的重要部分。隻要最終步長為1任何步長序列都可以工作。
算法最開始以一定的步長進行排序。然後會繼續以一定步長進行排序,最終算法以步長為1進行排序。當步長為1時,算法變為插入排序,這就保證了資料一定會被排序。
Donald Shell 最初建議步長選擇為N/2并且對步長取半直到步長達到1。雖然這樣取可以比O(N2)類的算法(插入排序)更好,但這樣仍然有減少平均時間和最差時間的餘地。可能希爾排序最重要的地方在于當用較小步長排序後,以前用的較大步長仍然是有序的。比如,如果一個數列以步長5進行了排序然後再以步長3進行排序,那麼該數列不僅是以步長3有序,而且是以步長5有序。如果不是這樣,那麼算法在疊代過程中會打亂以前的順序,那就
不會以如此短的時間完成排序了。
| 步長序列 | 最壞情況下複雜度 |
| | |
| | |
| | |
已知的最好步長序列是由Sedgewick提出的(1, 5, 19, 41, 109,...),該序列的項來自
這兩個算式。
這項研究也表明“比較在希爾排序中是最主要的操作,而不是交換。”用這樣步長序列的希爾排序比插入排序和堆排序都要快,甚至在小數組中比快速排序還快,但是在涉及大量資料時希爾排序還是比快速排序慢。
算法穩定性
由上文的希爾排序算法示範圖即可知,希爾排序中相等資料可能會交換位置,是以希爾排序是不穩定的算法。
直接插入排序和希爾排序的比較
直接插入排序是穩定的;而希爾排序是不穩定的。
直接插入排序更适合于原始記錄基本有序的集合。
希爾排序的比較次數和移動次數都要比直接插入排序少,當N越大時,效果越明顯。
在希爾排序中,增量序列gap的取法必須滿足:最後一個步長必須是 1 。
直接插入排序也适用于鍊式存儲結構;希爾排序不适用于鍊式結構。
完整參考代碼
JAVA版本
代碼實作
範例代碼中的初始序列和本文圖示中的序列完全一緻。
1 package notes.javase.algorithm.sort;
2
3 public class ShellSort {
4 public void shellSort(int[] list) {
5 int gap = list.length / 2;
6
7 while (1 <= gap) {
8 // 把距離為 gap 的元素編為一個組,掃描所有組
9 for (int i = gap; i < list.length; i++) {
10 int j = 0;
11 int temp = list[i];
12
13 // 對距離為 gap 的元素組進行排序
14 for (j = i - gap; j >= 0 && temp < list[j]; j = j - gap) {
15 list[j + gap] = list[j];
16 }
17 list[j + gap] = temp;
18 }
19
20 System.out.format("gap = %d:\t", gap);
21 printAll(list);
22 gap = gap / 2; // 減小增量
23 }
24 }
25
26 // 列印完整序列
27 public void printAll(int[] list) {
28 for (int value : list) {
29 System.out.print(value + "\t");
30 }
31 System.out.println();
32 }
33
34 public static void main(String[] args) {
35 int[] array = {
36 9, 1, 2, 5, 7, 4, 8, 6, 3, 5
37 };
38
39 // 調用希爾排序方法
40 ShellSort shell = new ShellSort();
41 System.out.print("排序前:\t\t");
42 shell.printAll(array);
43 shell.shellSort(array);
44 System.out.print("排序後:\t\t");
45 shell.printAll(array);
46 }
47 }
View Code
運作結果
排序前: 9 1 2 5 7 4 8 6 3 5
gap = 5: 4 1 2 3 5 9 8 6 5 7
gap = 2: 2 1 4 3 5 6 5 7 8 9
gap = 1: 1 2 3 4 5 5 6 7 8 9
排序後: 1 2 3 4 5 5 6 7 8 9
參考資料
《資料結構習題與解析》(B級第3版)
維基百科-希爾排序:http://zh.wikipedia.org/zh-cn/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F
相關閱讀
歡迎閱讀 程式員的内功——算法 系列
示例源碼:https://github.com/dunwu/algorithm-notes