題目連結:http://poj.org/problem?id=2653
Time Limit: 3000MS Memory Limit: 65536K
Description
Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.
Input
Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
The picture to the right below illustrates the first case from input.
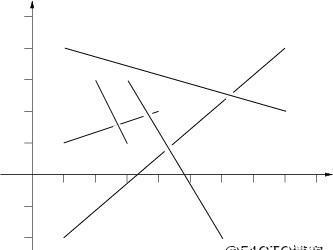
5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0 Sample Output
Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3. Hint
Huge input,scanf is recommended.
題意:
給出n根細木棍的坐标,每次按順序放到指定坐标位置,這樣會導緻一些後放的木棍壓倒前面的木棍;
求最後那些木棍沒有被壓住。
題解:
剛開始我是每輸入第i跟木棍,就周遊1 ~ i-1的木棍,看看他們有沒有被壓住,但這樣最後TLE了;
看Dis裡說,先全部輸入,然後枚舉,對第i根木棍,周遊i+1 ~ n的木棍,一旦出現壓住i的,就标記并且跳出;
明明感覺這樣不T很不科學,但就是AC了……奇怪……
AC代碼:
#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
const double eps = 1e-6;
struct Point{
double x,y;
Point(double tx=0,double ty=0):x(tx),y(ty){}
};
typedef Point Vctor;
//向量的加減乘除
Vctor operator + (Vctor A,Vctor B){return Vctor(A.x+B.x,A.y+B.y);}
Vctor operator - (Point A,Point B){return Vctor(A.x-B.x,A.y-B.y);}
Vctor operator * (Vctor A,double p){return Vctor(A.x*p,A.y*p);}
Vctor operator / (Vctor A,double p){return Vctor(A.x/p,A.y/p);}
int dcmp(double x)
{
if(fabs(x)<eps) return 0;
else return (x<0)?(-1):(1);
}
bool operator == (Point A,Point B){return dcmp(A.x-B.x)==0 && dcmp(A.y-B.y)==0;}
double Cross(Vctor A,Vctor B){return A.x*B.y-A.y*B.x;}
//判斷線段是否規範相交
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)
{
double c1 = Cross(a2 - a1,b1 - a1), c2 = Cross(a2 - a1,b2 - a1),
c3 = Cross(b2 - b1,a1 - b1), c4 = Cross(b2 - b1,a2 - b1);
return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0;
}
int n;
struct Seg{
Point a,b;
bool pressed;
}seg[100005];
int main()
{
while(scanf("%d",&n) && n!=0)
{
for(int i=1;i<=n;i++)
{
scanf("%lf%lf%lf%lf",&seg[i].a.x,&seg[i].a.y,&seg[i].b.x,&seg[i].b.y);
seg[i].pressed=0;
}
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)
{
if(SegmentProperIntersection(seg[i].a,seg[i].b,seg[j].a,seg[j].b))
{
seg[i].pressed=1;
break;
}
}
}
printf("Top sticks: ");
for(int i=1,cnt=1;i<=n;i++)
{
if(seg[i].pressed) continue;
if(cnt!=1) printf(", ");
printf("%d",i);
cnt++;
}
printf(".\n");
}
} View Code