實驗8 最小生成樹
實驗目的
- 掌握圖的存儲結構
- 掌握圖最小生成樹的普裡姆或克魯斯卡爾算法及實作
實驗内容
- 從檔案中讀入無向圖(網)并以鄰接矩陣存儲
- 利用普裡姆算法構造最小生成樹
代碼
tu.txt (教程P166 圖6.19)
6 10
A B C D E F
A B 6
B E 3
E F 6
F D 2
D A 5
A C 1
B C 5
E C 6
F C 4
D C 5
prim.cpp
#include <iostream>
#include <fstream>
using namespace std;
#define MVNum 10
#define MaxInt 32767 // 表示極大值 ∞
#define GRAPH_FILE "./tu.txt" // 輸入的檔案路徑
using VerTexType = char;
using ArcType = int;
// 輔助數組,用來記錄從頂點集U到V-U的權值最小的邊
struct
{
VerTexType adjvex; //最小邊在U中的那個頂點
ArcType lowcost; //最小邊上的權值
} closedge[MVNum];
struct AMGraph
{
VerTexType vexs[MVNum]; //頂點表
ArcType arcs[MVNum][MVNum]; //鄰接矩陣
int vexnum, arcnum; //圖的目前點數和邊數
};
// 确定點v在G中的位置
int LocateVex(AMGraph &G, VerTexType v)
{
for (int i = 0; i < G.vexnum; ++i)
if (G.vexs[i] == v)
return i;
return -1;
}
//采用鄰接矩陣表示法,建立無向網G
void CreateUDN(AMGraph &G)
{
fstream file(GRAPH_FILE);
if (!file)
{
cout << "沒有找到圖檔案!" << endl;
exit(-1);
}
file >> G.vexnum >> G.arcnum; //輸入總頂點數,總邊數
for (int i = 0; i < G.vexnum; ++i)
file >> G.vexs[i];
// 初始化鄰接矩陣,邊的權值均置為極大值 MaxInt
for (int i = 0; i < G.vexnum; ++i)
for (int j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = MaxInt;
// 構造鄰接矩陣
for (int k = 0; k < G.arcnum; ++k)
{
VerTexType v1, v2;
ArcType weight;
file >> v1 >> v2 >> weight; //輸入一條邊依附的頂點
int i = LocateVex(G, v1);
int j = LocateVex(G, v2); //确定v1和v2在G中的位置,即頂點數組的下标
G.arcs[j][i] = G.arcs[i][j] = weight; // 置<v1, v2>的對稱邊<v2, v1>的權值為w
}
file.close();
}
// 傳回還沒加入生成樹的, 權值最小的點
int Min(AMGraph &G)
{
int index = -1;
int min = MaxInt;
for (int i = 0; i < G.vexnum; ++i)
{
// lowcast == 0 說明這個點已經加入生成樹
if ((closedge[i].lowcost != 0) && closedge[i].lowcost < min)
{
min = closedge[i].lowcost;
index = i;
}
}
return index;
}
// 無向網G以鄰接矩陣形式存儲,從頂點u出發構造G的最小生成樹T,輸出T的各條邊
int MiniSpanTree_Prim(AMGraph &G, VerTexType u)
{
int lowcost_sum = 0;
int start = LocateVex(G, u); // 起點下标
// 初始化輔助數組
for (int i = 0; i < G.vexnum; i++)
{
if (start == i)
closedge[i].lowcost = 0; // 起點加入生成樹, 代價是 0(作為加入生成樹的标記)
else
closedge[i] = {u, G.arcs[start][i]}; // u 到其它結點 i 的代價為對應權值
}
// 通過 n - 1 輪循環, 把剩下的點加到生成樹裡面
for (int i = 1; i < G.vexnum; ++i)
{
int k = Min(G); // 找一個沒有加入生成樹的, 代價最小的點
lowcost_sum += closedge[k].lowcost;
closedge[k].lowcost = 0; // 第k個頂點并入U集(加入生成樹)
VerTexType u0 = closedge[k].adjvex; // u0為最小邊的一個頂點,u0∈ U
VerTexType v0 = G.vexs[k]; // v0為最小邊的另一個頂點,v0∈ V-U
cout << "邊 " << u0 << "--->" << v0 << endl; // 輸出目前的最小邊(u0, v0)
// 現在以 k 為起點, 把和它相鄰的沒有加入生成樹的結點最小代價更新一下
for (int j = 0; j < G.vexnum; ++j)
if (G.arcs[k][j] < closedge[j].lowcost) // 如果結點 j 通過 k 接入生成樹的代價 < 之前把 j 加入生成樹的最小代價
closedge[j] = {G.vexs[k], G.arcs[k][j]}; // 記錄結點 j 的最小代價, 來源邊是 k
}
return lowcost_sum;
}
int main()
{
cout << "************算法6.8 普裡姆算法**************" << endl;
AMGraph G;
CreateUDN(G);
cout << "無向圖G建立完成!" << endl;
cout << "******利用普裡姆算法構造最小生成樹結果:******" << endl;
VerTexType start = 'A';
int lowcost_sum = MiniSpanTree_Prim(G, start);
cout << "以" << start << "為起點構造最小生成樹, 代價為: " << lowcost_sum << endl;
cout << endl;
return 0;
}
截圖
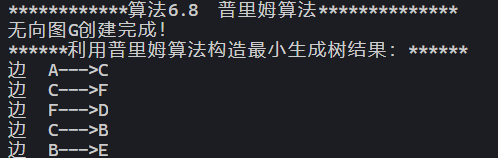 8.最小生成樹
8.最小生成樹 