相關:
第一數學歸納法 vs 第二數學歸納法 vs 良序定理
第二數學歸納法:硬币問題和堆垛遊戲
第一數學歸納法:施塔特中心的地闆磚
良序原理:算術基本定理的證明
*數學歸納法是一種顯示(局部)自然數元素都具有某種性質的有力工具。在離散數學和計算機科學中它都起到了重要作用。事實上,它的使用本身就是對離散性質的一種定義。歸納法的缺點在于它無法告訴你“究竟發生了什麼”,即性質成立的根本原因,不過這也是它的一個優點,降低了證明的複雜性。*
在這篇博文和之後的博文中我會通過一些有意思的問題介紹數學歸納法中的第一數學歸納法和第二數學歸納法以及不變性原理(歸納法的一種,通常被用在step-by-step的推理過程中),并在最後總結良序原理、第一數學歸納法和第二數學歸納法的聯系。
第一數學歸納法(Ordinary Induction): 設P是對于非負整數的一個謂語,則
- P(0)成立
- 對于所有的非負整數n,P(n) -> p(n + 1)
- 則對于所有的非負整數m,P(m)成立
看起來這個方法非常簡單,以至于我們可能找不到能證明它的正确性的公理(實際上它和良序原理是等價的)。用公式表示就是:
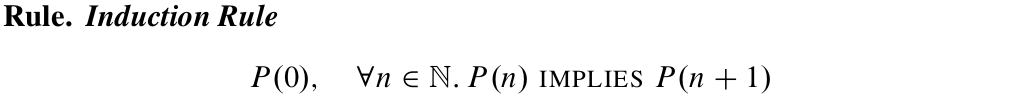
通常而言,使用第一數學歸納法都可以遵循下面這個模版:
- 聲明接下來的證明會采用歸納法。
- 定義正确的謂詞P,P(n)通常被稱作“歸納假設”。歸納最後得到的結論就是對于所有非負整數p(n)均成立。一個清晰的歸納假設通常是歸納法中最重要的一步,是以不要簡寫!簡單的情況下P就是你要證明的東西,但有些時候P可能會包含一些變量,這個時候就要說明清楚哪一個是n。
- 證明P(0)成立。
- 證明對于所有非負整數n,P(n) -> P(n + 1)。即假設P(n)成立,然後利用P(n)成立這個假設推出p(n + 1)也是成立的。要注意的是,我們必須保證P(n) -> P(n + 1)對于所有非負整數都是能夠成立的,即“推理鍊條”不能被中斷(本文最後會有一個反面例子)。
- 由歸納法得出結論。
**施塔特中心的地闆磚問題(應該是一個真實的事): **
幾年前MIT打算建一座名叫施塔特中心的建築物,但是在建築過程中發生了資金不足的情況。校董事會商議後決定邀請社會人士捐款,并為捐款最多的一位做一座雕像B立在大廳。這個建築的設計師設計的大廳形狀是一個由瓷磚鋪成的長寬為2^n的正方形,而且采用的瓷磚也很特别,是一個由三個1 * 1正方形組成的L形瓷磚,如下圖所示:
設計師還要求,雕像B隻能立在大廳的正中心(對于n=0,整個大廳就是那一個雕像,其餘的情況雕像必須放在中心的2 * 2的空間内),其中n = 2的情況如下圖所示:
設計師的方案對于n的取值又要求嗎?還是說對于任意非負整數n都能滿足呢?
下面利用第一數學歸納法對其進行證明:
- 本次證明采用數學第一歸納法
- 設謂詞P(n)為對于非負整數n,設計師的要求能夠滿足。
- P(0)成立因為B雕像占據了整個大廳(不需要鋪瓷磚)。
- 假設P(n)成立,即對于一個2^n長寬的正方形,我們可以把B雕像放在中心位置,其餘的部分鋪上L形瓷磚。
這個時候問題發生了,我們不能由P(n)推出P(n + 1),因為我們隻能得到可以在2^(n + 1)的正方形中心的四個對角方向的“中心”可以放置B雕像。
當這種情況發生時,首先的想法應該是找一個更加普遍或者說強壯的歸納假設,也就是之前歸納假設的超集。例如在這題中,我們可以把P(n)變為對于一個2^n長寬的正方形,我們可以把B雕像放在其中的任意位置,其餘的部分鋪上L形瓷磚。
這看起來有些奇怪——“如果你證明不了A,那就證明比A更普遍的B”——但是在歸納法中确實是這樣的,因為我們在推P(n + 1)的時候也可以獲得更好的條件。當然,增強後的P(n)首先要是(至少感覺上)是正确的。下面就采用增強後的P來證明:
- 設謂詞P(n)為對于非負整數n,可以把B雕像放2^n正方形的任意位置,其餘的部分鋪上L形瓷磚。。
- 假設P(n)成立,即對于一個2^n長寬的正方形,我們可以把B雕像放在其中的任意位置,其餘的部分鋪上L形瓷磚。那麼對于P(n + 1),即一個2(n+1)長寬的正方形,我們可以将其分為四個2n的正方形,而對于其中的每個正方形,由于P(n)成立,我們将其中的三個正方形的對角的那個1*1正方形空出來,在2(n+1)的正方形中心形成一個L形,并鋪上一塊瓷磚,這個時候我們就可以在剩下的那個2n的正方形中任意放置B雕像了,如下圖所示: 由于這三個2n的正方形選擇是随機的,是以可以得出結論,即我們可以在2(n+1)的正方形任意位置放置B雕像,其餘部分鋪上L形瓷磚。
第一數學歸納法:施塔特中心的地闆磚
5.由歸納法得出對于非負整數n,我們可以把B雕像放在一個2^n長寬的正方形中的任意位置,其餘的部分鋪上L形瓷磚。
是以我們當然也可以把雕像放在中心位置了。可以看到,我們不僅證明了一個更強的結論,還找到了實作這種結論的算法。
如前面所說,在進行p(n) -> p(n + 1)這步時,我們必須保證P(n) -> P(n + 1)對于所有非負整數都是能夠成立的,即“推理鍊條”不能被中斷。這裡舉出一個有名的反面教材,證明所有的馬都是一種顔色:
1.本次證明使用第一數學歸納法。
2.設命題P(n)為對于任意n匹馬(n>=1),它們的顔色一樣。
3.這個命題對n=1時成立,即,隻有1匹馬時,馬的顔色隻有一種。
4.假設這個命題對n成立,即假設任何n匹馬都是一種顔色。那麼當我們有n+1匹馬時,不妨把它們編好号:
1, 2, 3……n, n+1 ,對其中(1、2……n)這些馬,由我們的假設可以得到,它們都是同一種顔色;對(2、3……n、n+1)這些馬,我們也可以得到它們是一種顔色;由于這兩組中都有(2、3、……n)這些馬,是以可以得到,這n+1種馬都是同一種顔色。即P(n) -> p(n + 1)
5.得到所有的馬顔色相同。
這個證明的錯誤來于推理的第二步:當n=1時,n+1=2,此時馬的編号隻有1、2,那麼分的兩組是(1)和(2)——它們沒有交集,是以第二步的推論是錯誤的。數學歸納法第二步要求n→n+1過程對n=1,2,3……的數都成立,而上面的證明就好比多米諾骨牌的第一塊和第二塊之間間隔太大,推倒了第一塊,但它不會推倒第二塊。即使我們知道第二塊倒下會推倒第三塊等等,但這個過程早已在第一和第二塊之間就中斷了。
參考:
- Mathematics for Computer Science
- 數學歸納法