相關:
第一數學歸納法 vs 第二數學歸納法 vs 良序定理
第二數學歸納法:硬币問題和堆垛遊戲
第一數學歸納法:施塔特中心的地闆磚
良序原理:算術基本定理的證明
*第二數學歸納法證明的結論和[第一數學歸納法](http://www.cnblogs.com/liqiuhao/p/7792374.html)是一樣的,都是證明(局部)非負數元素都具有某些性質。但是第二數學歸納法中P(n)的推理是基于P(0~n)而非僅僅是P(n)。*
第二數學歸納法(Strong Induction),設P是作用在非負整數的謂詞:
- P(0)成立
- 對于所有的n,P(0), P(1), P(2) ... P(n)共同推出P(n + 1)
- 則對于所有的非負整數m,P(m)成立
可以看到,在使用第一數學歸納法的時候我們隻用了P(n),而第二數學歸納法相比于第一數學歸納法在推P(n + 1)的時候使用更多的假設(P(0), P(1), P(2) ... P(n) ),用公式表達如下:
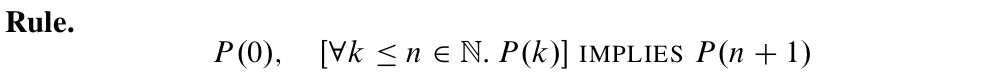
第二數學歸納法使用的模版和第一數學歸納法很像,除了兩個地方:
- 聲明證明使用的是第二數學歸納法
- 推理部分要假設P(0), P(1), P(2) ... P(n) 都是正确的。
硬币問題:
在太平洋上有一個叫做Inductia的國家,他們使用一種叫做Strong的硬币(簡稱Sg)。當年在印刷這種硬币的時候由于經費問題就隻印刷了面值為3Sg和5Sg的硬币。雖然當地居民在找小額零錢(例如4Sg或者7Sg)的時候會有一些麻煩,但是他們發現任何大于等于8Sg的面額都能使用這兩種硬币找開,例如26Sg可以用下面這種方案:
請給出證明。
- 下面使用第二數學歸納法證明。
- 設P(n)為對于8+n面額的錢,居民們可以用3Sg和5Sg的硬币找開。
- 當n=0,8Sg = 5Sg + 3Sg,是以P(0)成立。
- 設p(0),p(1),p(2) ... p(n)均成立(n > 2),證明p(n + 1)成立:對于8 + n + 1的面額,可以前将其變為(8 + n + 1 - 3) + 3即(8 + n - 2) + 3這樣的面額,由于我們已經假設了P(n - 2)的成立,是以(8 + n - 2) + 3可以由P(n - 2)的方案加上一個3Sg的硬币組合而成,是以P(n + 1)成立。對于n <=2:n = 2時,10 = 5 + 5;n = 1時,9 = 3*3。(這裡要注意将n小于等于2的情況分開讨論,因為P(n-2)在n<2的時候沒有定義,即歸納推理的“鍊條”不能斷)
- 由歸納法,所有大于等于8Sg的面額居民都能用這兩種硬币找開。
注:這個問題本質上是因為5和3的最大公因數是1,是以它們的線性組合可以得出任何數(1的整數倍),另外在5*1 + 3*1 = 8以上的任何數都可以用5a + 3b 表示,其中a和b都是非負數。後面我寫數論部分的時候會給出具體證明的。
堆垛遊戲:
在你的面前是一個由n個木塊堆起來的堆垛,你每次可以将一個堆拆成兩個堆,除非這個堆隻剩下了一個木塊。在每次分拆一個堆的時候你可以獲得一些分數,例如,你将一個a+b塊木塊的堆拆成了a塊的堆和b塊的堆,你就可以得到a*b分。直到所有的堆都隻含一個木塊,遊戲結束。例如,下圖顯示了一個拆一個由10個木塊組成的堆的一種方案,其得分為45分 :
設請問你該采取什麼政策能獲得最高的分數?
我的第一想法是每次都把堆拆成兩個相同高度的堆或者相差為1,例如5*5 = 25 > 1 * 9,但随後我意識到雖然第一次可能會大,但是随後可能會比較小,例如2 * 3 < 1 * 8。聯想到這個題是要用歸納法的,自然覺得可能和政策無關,即不管什麼政策都會得到相同的分數。試一下上面這個例子,每次都隻拿走一個木塊:9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45,果然是這樣,其中1+2+3 ... +n = (n+1)*n/2,下面證明:
- 以下證明使用第二數學歸納法。
- 設P(n)為對于木塊數為n的堆垛,其得分為n*(n+1)/2,和政策無關。
- P(0) = 0,即0*(0+1)/2 = 0,成立。
- 設P(1), P(2), P(3) ... P(n)成立。對于P(n + 1),假設我們拆的第一步将其分為了木塊數分别為a和b的兩個堆,第一次得分為a*b,由于a和b都小于n+1,由P(a)和P(b)成立,我們可以知道最終的總得分為第一次的得分ab加上拆剩下兩個堆的分數之和:ab + a*(a+1)/2 + b*(b+1)/2 = (a^2 + b^2 + ab + a + b)/2 = (a^2 + b^2 +2ab + n + 1)/2 = ( (a+b)^2 + (n+1) )/2 = ((n+1)^2 + (n+1))/2 = (n+1 + 1)(n+1)/2。是以推得P(n+1)成立。
- 由歸納法得到對于任意非負整數n,這個遊戲的最終得分都是n*(n+1)/2,和政策無關。
參考:
- Mathematics for Computer Science