判斷點在多邊形内算法的C++實作

介紹了使用射線法判斷點在多邊形内部還是外部的算法，并通過C/C++做了具體實作。

目錄

• 1. 算法思路
• 2. 具體實作
• 3. 改進空間

判斷平面内點是否在多邊形内有多種算法，其中射線法是其中比較好了解的一種，而且能夠支援凹多邊形的情況。該算法的思路很簡單，就是從目标點出發引一條射線，看這條射線和多邊形所有邊的交點數目。如果有奇數個交點，則說明在内部，如果有偶數個交點，則說明在外部。如下圖所示：

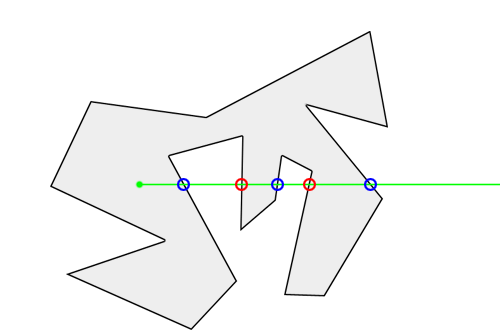
算法步驟如下：

1. 已知點point(x,y)和多邊形Polygon的點有序集合（x1,y1;x2,y2;….xn,yn;）；

2. 以point為起點，以無窮遠為終點作平行于X軸的射線line(x,y; -∞,y)；循環取得多邊形的每一條邊side(xi,yi;xi+1,yi+1)：

   1). 判斷point(x,y)是否在side上，如果是，則傳回true。

   2). 判斷line與side是否有交點，如果有則count++。

3. 判斷交點的總數count，如果為奇數則傳回true，偶數則傳回false。

在具體的實作過程中，其實還有一個極端情況需要注意：當射線line經過的是多邊形的頂點時，判斷就會出現異常情況。針對這個問題，可以規定線段的兩個端點，相對于另一個端點在上面的頂點稱為上端點，下面是下端點。如果射線經過上端點，count加1，如果經過下端點，則count不必加1。具體實作如下：

#include<iostream>
#include <cmath>
#include <vector>
#include <algorithm>

#define EPSILON 0.000001

using namespace std;

//二維double矢量
struct  Vec2d
{
	double x, y;

	Vec2d()
	{
		x = 0.0;
		y = 0.0;
	}
	Vec2d(double dx, double dy)
	{
		x = dx;
		y = dy;
	}
	void Set(double dx, double dy)
	{
		x = dx;
		y = dy;
	}
};

//判斷點線上段上
bool IsPointOnLine(double px0, double py0, double px1, double py1, double px2, double py2)
{
	bool flag = false;
	double d1 = (px1 - px0) * (py2 - py0) - (px2 - px0) * (py1 - py0);
	if ((abs(d1) < EPSILON) && ((px0 - px1) * (px0 - px2) <= 0) && ((py0 - py1) * (py0 - py2) <= 0))
	{
		flag = true;
	}
	return flag;
}

//判斷兩線段相交
bool IsIntersect(double px1, double py1, double px2, double py2, double px3, double py3, double px4, double py4)
{
	bool flag = false;
	double d = (px2 - px1) * (py4 - py3) - (py2 - py1) * (px4 - px3);
	if (d != 0)
	{
		double r = ((py1 - py3) * (px4 - px3) - (px1 - px3) * (py4 - py3)) / d;
		double s = ((py1 - py3) * (px2 - px1) - (px1 - px3) * (py2 - py1)) / d;
		if ((r >= 0) && (r <= 1) && (s >= 0) && (s <= 1))
		{
			flag = true;
		}
	}
	return flag;
}

//判斷點在多邊形内
bool Point_In_Polygon_2D(double x, double y, const vector<Vec2d> &POL)
{	
	bool isInside = false;
	int count = 0;
	
	//
	double minX = DBL_MAX;
	for (int i = 0; i < POL.size(); i++)
	{
		minX = std::min(minX, POL[i].x);
	}

	//
	double px = x;
	double py = y;
	double linePoint1x = x;
	double linePoint1y = y;
	double linePoint2x = minX -10;			//取最小的X值還小的值作為射線的終點
	double linePoint2y = y;

	//周遊每一條邊
	for (int i = 0; i < POL.size() - 1; i++)
	{	
		double cx1 = POL[i].x;
		double cy1 = POL[i].y;
		double cx2 = POL[i + 1].x;
		double cy2 = POL[i + 1].y;
				
		if (IsPointOnLine(px, py, cx1, cy1, cx2, cy2))
		{
			return true;
		}

		if (fabs(cy2 - cy1) < EPSILON)   //平行則不相交
		{
			continue;
		}

		if (IsPointOnLine(cx1, cy1, linePoint1x, linePoint1y, linePoint2x, linePoint2y))
		{
			if (cy1 > cy2)			//隻保證上端點+1
			{
				count++;
			}
		}
		else if (IsPointOnLine(cx2, cy2, linePoint1x, linePoint1y, linePoint2x, linePoint2y))
		{
			if (cy2 > cy1)			//隻保證上端點+1
			{
				count++;
			}
		}
		else if (IsIntersect(cx1, cy1, cx2, cy2, linePoint1x, linePoint1y, linePoint2x, linePoint2y))   //已經排除平行的情況
		{
			count++;
		}
	}
	
	if (count % 2 == 1)
	{
		isInside = true;
	}

	return isInside;
}


int main()
{	
	//定義一個多邊形（六邊形）
	vector<Vec2d> POL;	
	POL.push_back(Vec2d(268.28, 784.75));
	POL.push_back(Vec2d(153.98, 600.60));
	POL.push_back(Vec2d(274.63, 336.02));
	POL.push_back(Vec2d(623.88, 401.64));
	POL.push_back(Vec2d(676.80, 634.47));
	POL.push_back(Vec2d(530.75, 822.85));
	POL.push_back(Vec2d(268.28, 784.75));				//将起始點放入尾部，友善周遊每一條邊
		
	//
	if (Point_In_Polygon_2D(407.98, 579.43, POL))
	{
		cout << "點（407.98, 579.43）在多邊形内" << endl;
	}
	else
	{
		cout << "點（407.98, 579.43）在多邊形外" << endl;
	}

	//
	if (Point_In_Polygon_2D(678.92, 482.07, POL))
	{
		cout << "點（678.92, 482.07）在多邊形内" << endl;
	}
	else
	{
		cout << "點（678.92, 482.07）在多邊形外" << endl;
	}

	return 0;
}
           

運作結果如下：

1. 很多情況下在使用該算法之前，需要一個快速檢測的功能：當點不在多邊形的外包矩形的時候，那麼點一定不在多邊形内。
2. 判斷點線上上函數IsPointOnLine()和判斷線段相交函數IsIntersect()這裡并不是最優算法，可以改成向量計算，效率應該更高。