跳表介紹 #NoSQL #算法 #Redis #報表介紹 #介紹消息處理 #介紹消息 #加密介紹 #介紹行業

跳躍表（英文名：Skip List），于 1990 年 William Pugh 發明，是一個可以在有序元素中實作快速查詢的資料結構，其插入，查找，删除操作的平均效率都為 $O(logn)$。

跳躍表的整體性能可以和二叉查找樹（AVL 樹，紅黑樹等）相媲美，其在 Redis 和 LevelDB 中都有廣泛的應用。

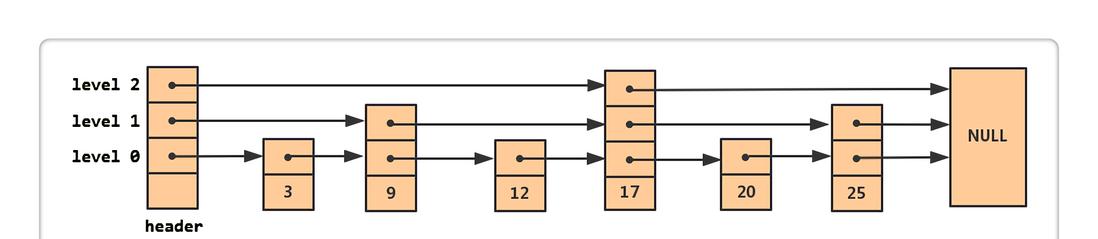
每個結點除了資料域，還有若幹個指針指向下一個結點。

整體上看，Skip List 就是帶有層級結構的連結清單（結點都是排好序的），最下面一層（level 0）是所有結點組成的一個連結清單，依次往上，每一層也都是一個連結清單。不同的是，它們隻包含一部分結點，并且越往上結點越少。仔細觀察你會發現，通過增加層數，從目前結點可以直接通路更遠的結點（這也就是 Skip List 的精髓所在），就像跳過去一樣，是以取名叫 Skip List（跳躍表）。

過程分析

先來看下跳躍表的整體代碼結構：

#define P 0.25
#define MAX_LEVEL 32

struct Node
{
    int key;
    Node ** forward;
    Node(int key = 0, int level = MAX_LEVEL)
    {
        this->key = key;
        forward = new Node*[level];
        memset(forward, 0, level * sizeof(Node*));
    }
};

class SkipList
{
private:
    Node * header;
    int level;
private:
    int random_level();
public:
    SkipList();
    ~SkipList();
    bool insert(int key);
    bool find(int key);
    bool erase(int key);
    void print();
};

2.1、插入

首先，我們要找到 10 在每一層應該被插入的位置，是以需要一個臨時數組 update[] 來記錄位置資訊。

其次，我們要确定結點 10 的層數（結點 9 的層數為 2，結點 12 的層數為 1）。

理想的跳躍表結構是：第一層有全部的結點，第二層有 1 2 的結點，且是均勻間隔的，第三層有 1 4 的結點，且也是均勻間隔的...，那麼整個表的層數就是 $logn$。每一次插入一個新結點時，最好的做法就是根據目前表的結構得到一個合适的層數，插入後可以讓跳躍表盡量接近理想的結構，但這在實作上會非常困難。Pugh 的論文中提出的方法是根據機率随機為新結點生成一個層數，具體的算法如下：

給定一個機率 p（p 小于 1），産生一個 [0,1) 之間的随機數；
如果這個随機數小于 p，則層數加 1；
重複以上動作，直到随機數大于機率 p（或層數大于程式給定的最大層數限制）。

雖然随機生成的層數會打破理想結構，但這種結構的期望複雜度依舊是 $O(logn)$，稍後文尾會給出證明。

最後，把結點 10 和它的前後結點連起來就行了。

int SkipList::random_level()
{
    int level = 1;

    while ((rand() & 0xffff) < (P * 0xffff) && level < MAX_LEVEL)
        level++;

    return level;
}

bool SkipList::insert(int key)
{
    Node * node = header;
    Node * update[MAX_LEVEL];
    memset(update, 0, MAX_LEVEL * sizeof(Node*));

    // 找到該結點在每一層應該被插入的位置
    for (int i = level - 1; i >= 0; i--)
    {
        while (node->forward[i] && node->forward[i]->key < key)
            node = node->forward[i];

        update[i] = node;
    }

    node = node->forward[0];

    if (node == nullptr || node->key != key)
    {
        int new_level = random_level();

        // 若新生成的層數比之前的大，那麼高出的部分需特殊處理
        if (new_level > level)
        {
            for (int i = level; i < new_level; i++)
                update[i] = header;

            level = new_level;
        }

        Node * new_node = new Node(key, new_level);

        // 前後結點連接配接起來
        for (int i = 0; i < new_level; i++)
        {
            new_node->forward[i] = update[i]->forward[i];
            update[i]->forward[i] = new_node;
        }

        return true;
    }

    return false;
}

2.2 查找

查找操作很簡單，例如上圖，現要查找 20，

從最高層開始找，17 < 20，繼續往後，發現是 NULL，則往下一層繼續查找；
25 > 20，則往下一層繼續查找；
找到 20。

bool SkipList::find(int key)
{
    Node * node = header;

    for (int i = level - 1; i >= 0; i--)
    {
        while (node->forward[i] && node->forward[i]->key <= key)
            node = node->forward[i];

        if (node->key == key)
            return true;
    }

    return false;
}

2.3、删除

删除操作跟插入操作類似。首先找到我們要删除結點的位置，在查找時使用臨時空間來記錄結點在每一層的位置，接着就是逐層的連結清單删除操作。最後記住要釋放空間。删除結點之後，如果最高層沒有結點存在，那麼相應的，跳躍表的層數就應該降低。

bool SkipList::erase(int key)
{
    Node * node = header;
    Node * update[MAX_LEVEL];
    memset(update, 0, MAX_LEVEL * sizeof(Node*));

    // 找到要删除結點的位置
    for (int i = level - 1; i >= 0; i--)
    {
        while (node->forward[i] && node->forward[i]->key < key)
            node = node->forward[i];
        update[i] = node;
    }

    node = node->forward[0];

    if (node && node->key == key)
    {
        // 把待删除結點的前後結點連接配接起來
        for (int i = 0; i < level; i++)
            if (update[i]->forward[i] == node)
                update[i]->forward[i] = node->forward[i];

        delete node;

        // 如果最高層沒有結點存在，那麼相應的，跳躍表的層數就應該降低
        for (int i = level - 1; i >= 0; i--)
        {
            if (header->forward[i] == nullptr)
                level--;
            else
                break;
        }
    }

    return false;
}

完整代碼

#include <iostream>
#include <cstdlib>
#include <cstring>

#define P 0.25
#define MAX_LEVEL 32

using namespace std;

struct Node
{
    int key;
    Node ** forward;
    Node(int key = 0, int level = MAX_LEVEL)
    {
        this->key = key;
        forward = new Node*[level];
        memset(forward, 0, level * sizeof(Node*));
    }
};

class SkipList
{
private:
    Node * header;
    int level;
private:
    int random_level();
public:
    SkipList();
    ~SkipList();
    bool insert(int key);
    bool find(int key);
    bool erase(int key);
    void print();
};

int SkipList::random_level()
{
    int level = 1;

    while ((rand() & 0xffff) < (P * 0xffff) && level < MAX_LEVEL)
        level++;

    return level;
}

SkipList::SkipList()
{
    header = new Node;
    level = 0;
}

SkipList::~SkipList()
{
    Node * cur = header;
    Node * next = nullptr;

    while (cur)
    {
        next = cur->forward[0];
        delete cur;
        cur = next;
    }

    header = nullptr;
}

bool SkipList::insert(int key)
{
    Node * node = header;
    Node * update[MAX_LEVEL];
    memset(update, 0, MAX_LEVEL * sizeof(Node*));

    // 找到該結點在每一層應該被插入的位置
    for (int i = level - 1; i >= 0; i--)
    {
        while (node->forward[i] && node->forward[i]->key < key)
            node = node->forward[i];

        update[i] = node;
    }

    node = node->forward[0];

    if (node == nullptr || node->key != key)
    {
        int new_level = random_level();

        // 若新生成的層數比之前的大，那麼高出的部分需特殊處理
        if (new_level > level)
        {
            for (int i = level; i < new_level; i++)
                update[i] = header;

            level = new_level;
        }

        Node * new_node = new Node(key, new_level);

        // 前後結點連接配接起來
        for (int i = 0; i < new_level; i++)
        {
            new_node->forward[i] = update[i]->forward[i];
            update[i]->forward[i] = new_node;
        }

        return true;
    }

    return false;
}

bool SkipList::find(int key)
{
    Node * node = header;

    for (int i = level - 1; i >= 0; i--)
    {
        while (node->forward[i] && node->forward[i]->key <= key)
            node = node->forward[i];

        if (node->key == key)
            return true;
    }

    return false;
}

bool SkipList::erase(int key)
{
    Node * node = header;
    Node * update[MAX_LEVEL];
    memset(update, 0, MAX_LEVEL * sizeof(Node*));

    // 找到要删除結點的位置
    for (int i = level - 1; i >= 0; i--)
    {
        while (node->forward[i] && node->forward[i]->key < key)
            node = node->forward[i];
        update[i] = node;
    }

    node = node->forward[0];

    if (node && node->key == key)
    {
        // 把待删除結點的前後結點連接配接起來
        for (int i = 0; i < level; i++)
            if (update[i]->forward[i] == node)
                update[i]->forward[i] = node->forward[i];

        delete node;

        // 如果最高層沒有結點存在，那麼相應的，跳躍表的層數就應該降低
        for (int i = level - 1; i >= 0; i--)
        {
            if (header->forward[i] == nullptr)
                level--;
            else
                break;
        }
    }

    return false;
}

void SkipList::print()
{
    Node * node = nullptr;

    for (int i = 0; i < level; i++)
    {
        node = header->forward[i];
        cout << "Level " << i << " : ";
        while (node)
        {
            cout << node->key << " ";
            node = node->forward[i];
        }
        cout << endl;
    }

    cout << endl;
}

int main()
{
    SkipList sl;

    // test "insert"
    sl.insert(3);
    sl.insert(9);
    sl.insert(1); sl.insert(1);
    sl.insert(4);
    sl.insert(2); sl.insert(2);
    sl.insert(5);
    sl.insert(6);
    sl.insert(7);
    sl.insert(8);
    sl.insert(10);
    sl.insert(11);
    sl.insert(12);
    sl.print();

    // test "find"
    cout << sl.find(50) << endl;
    cout << sl.find(2) << endl;
    cout << sl.find(7) << endl << endl;

    // test "erase"
    sl.erase(1);
    sl.print();
    sl.erase(10);
    sl.print();
    sl.erase(11);
    sl.print();

    return 0;
}

運作如下（注意：結點層數采用的是随機值，故不同電腦可能會有不同的運作結果）：

Level 0 : 1 2 3 4 5 6 7 8 9 10 11 12
Level 1 : 3 4 6 9 10 11
Level 2 : 4 10 11
Level 3 : 10 11
Level 4 : 10 11
Level 5 : 10 11
Level 6 : 10

0
1
1

Level 0 : 2 3 4 5 6 7 8 9 10 11 12
Level 1 : 3 4 6 9 10 11
Level 2 : 4 10 11
Level 3 : 10 11
Level 4 : 10 11
Level 5 : 10 11
Level 6 : 10

Level 0 : 2 3 4 5 6 7 8 9 11 12
Level 1 : 3 4 6 9 11
Level 2 : 4 11
Level 3 : 11
Level 4 : 11
Level 5 : 11

Level 0 : 2 3 4 5 6 7 8 9 12
Level 1 : 3 4 6 9
Level 2 : 4

效率分析與證明

首先回顧下插入操作中随機生成層數的函數：

#define P 0.25
#define MAX_LEVEL 32

int SkipList::random_level()
{
    int level = 1;

    while ((rand() & 0xffff) < (P * 0xffff) && level < MAX_LEVEL)
        level++;

    return level;
}

參考文獻:

https://segmentfault.com/a/1190000022545575 https://www.qtmuniao.com/2020/07/03/leveldb-data-structures-skip-list/ https://segmentfault.com/a/1190000023927761 https://syt-honey.github.io/2019/03/23/17-%E8%B7%B3%E8%A1%A8%EF%BC%9A%E4%B8%BA%E4%BB%80%E4%B9%88Redis%E4%B8%80%E5%AE%9A%E8%A6%81%E7%94%A8%E8%B7%B3%E8%A1%A8%E6%9D%A5%E5%AE%9E%E7%8E%B0%E6%9C%89%E5%BA%8F%E9%9B%86%E5%90%88%EF%BC%9F/ https://www.jianshu.com/p/d4c2accd30fc https://qimok.cn/787.html https://segmentfault.com/a/1190000021618668

Redis系列(七)底層資料結構之跳躍表

https://www.jianshu.com/p/9d8296562806

跳表介紹

過程分析

2.1、插入

完整代碼

效率分析與證明

繼續閱讀

查找算法學習之二分查找（Python版本）——BinarySearch

CQ V1.0分詞bates(基于雙數組tire樹)—應該是目前最快的中文分詞算法

Command Network(POJ 3164)---定根最小樹形圖模闆題題目描述輸入格式輸出格式輸入樣例輸出樣例分析源程式

supervisor 管理redis 和httpd 環境centos7

Redis簡介一(單機版)發展曆程Redis

開源低帶寬語音編解碼器

241 Different Ways to Add Parentheses（C代碼版）

【趨高機器視覺】機器視覺技術原了解析及解決方案

CSMA/CD1． CSMA/CD的概述2． CSMA 的工作原理3． CSMA/CD控制規程及特點4． CSMA/CD協定5． CSMA/CD的優點6．結束語

極大似然法(ML)與最大期望法(EM)

C++ 第十五周報告1--《冒泡法排序》

筆試面試題目：滑動視窗(二)

資料結構與算法（27）——排序（二）

Dijkstra--簡易版（最短路徑）

GitHub連夜封殺！這份阿裡 10W 字内部 Java 字面試手冊到底有多強？

hdu7108哈希