圖的應用——最小生成樹

最小生成樹

• 生成樹（極小連通子圖）：含有圖中全部n個頂點，但隻有n-1條邊。并且n-1條邊不能構成回路。

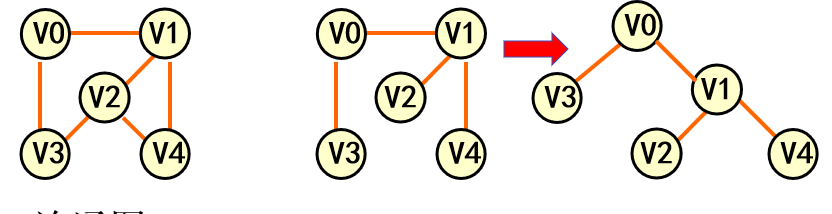
• 生成森林：非連通圖每個連通分量的生成樹一起組成非連通圖的生成森林。

求最小生成樹

• 使用不同的周遊圖的方法，可以得到不同的生成樹
• 從不同的頂點出發，也可能得到不同的生成樹。
• 按照生成樹的定義，n 個頂點的連通網絡的生成樹有 n 個頂點、n-1 條邊。

在網的多個生成樹中，尋找一個各邊權值之和最小的生成樹

構造最小生成樹的準則

• 必須隻使用該網中的邊來構造最小生成樹；
• 必須使用且僅使用n-1條邊來聯結網絡中的n個頂點
• 不能使用産生回路的邊

貪心算法(Greedy Algorithm)

• 算法原理：以目前情況為基礎作最優選擇，而不考慮各種可能的整體情況，是以貪心法不要回溯。
• 算法優點：因為省去了為尋找解而窮盡所有可能所必須耗費的大量時間，是以算法效率高。

貪婪算法的精神就是“隻顧如何獲得眼前最大的利益”,有時不一定是最優解。

Prim（普裡姆）算法

算法思想 —— 歸并頂點

• 在圖中任取一個頂點K作為開始點。令U={k}，W=V-U，其中V為圖中所有頂點集
• 在U中選取一個頂點，W中選取另一個頂點，使二者對應的邊是最短的一條。将該邊作為最小生成樹的邊儲存起來，并将該邊頂點全部加入U集合中，并從W中删去這些頂點。
• 重新調整U中頂點到W中頂點的距離， 使之保持最小，再重複此過程，直到W為空集止。

算法設計

• 在算法中需要設定一個輔助數組，對目前V－U集中的每個頂點，記錄和頂點集U中頂點相連接配接的代價最小的邊

struct {
    VertexType adjvex;  // U集中的頂點
    VRType lowcost;  // 邊的權值
} closedge[MAX_VERTEX_NUM];           

• lowcost[i]:表示以i為終點的邊的最小權值,當lowcost[i]=0說明以i為終點的邊的最小權值=0,也就是表示i點加入了MST
• adjvext[i]:表示對應lowcost[i]的起點，即說明邊<adjvex[i],i>是MST的一條邊，當adjvex[i]=0表示起點i加入MST

void MiniSpanTree_P(MGraph G, VertexType u){
    // 用普利姆算法從頂點u出發構造網G的最小生成樹
    k = LocateVex_MG(G, u);
    for(j = 0; j < G.vexnum; ++j)  // 輔助數組初始化
        if(j != k){
            closedge[j].adjvex = new char[10];
            strcpy(closedge[j].adjvex, G.vexs[k]);
            closedge[j].lowcost = G.arcs[k][j].adj;
        }
    closedge[k].lowcost = 0;  // 初始, U = {u}
    closedge[k].adjvex = new char[10];
    strcpy(closedge[k].adjvex, G.vexs[k]);
    for(i = 0; i > G.vexnum; i ++){
        // //繼續向生成樹上添加頂點
        mincost = INF;  // 找權值最小的頂點
        for(m = 0; m < G.vexnum; ++m)
            if(mincose > closedge[m].lowcost && closedge[m].lowcost != 0){
                mincose = closedge[m].lowcost;
                k = m;
            } // 求出加入生成樹的下一個頂點(k)
        if(closedge[k].lowcost != 0)
            //輸出生成樹上一條邊
            cout << closedge[k].adjvex << G.vexs[k] << closedge[k].lowcost;
        closedge[k].lowcost = 0; // 第k頂點并入U集
        for(j = 0; j < G.vexnum; j++)
            // 修改其它頂點的最小邊
            if(G.arcs[k][j].adj < closedge[j].lowcost){
                strcpy(closedge[j].adjvex, G.vexs[k]);
                closedge[j].lowcost = G.arcs[k][j].adj;
            }
    }
}           

KrusKal（克魯斯卡爾）算法

算法思想 —— 歸并邊

• 将圖中所有邊按權值遞增順序排列；
• 依次標明取權值較小的邊，但要求後面選取的邊不能與前面選取的邊構成回路，若構成回路，則放棄該條邊，再去選後面權值較大的邊，n個頂點的圖中，選夠n-1條邊即可。

構造非連通圖 ST=( V,{ } );

k = i = 0; // k 計選中的邊數

while (k<n-1) {

++i;

檢查邊集 E 中第 i 條權值最小的邊(u,v);

**若(u,v)加入ST後不使ST中産生回路，

則 輸出邊(u,v); 且 k++;**

}

typedef struct {
    // 增加邊結構定義
    int beginvex, endvex;  // 邊的起點、終點
    VRType cost;  // 邊的權值
} edgetype;

edgetype edges[MAX_VERTEX_NUM];

void MiniSpanTree_Kruskal(ALGraph &G){
    int parents[MAX_VERTEX_NUM];
    cin >> G.vexnum >> G.arcnum;  // 頂點數、弧數
    for(i = 0; i < G.vexnum; i++){
        // 建立頂點表
        G.vertices[i].data = new char[10];
        cin >> G.vertices[i].data;  // 讀入頂點資訊并初始化
        G.vertices[i].firstarc = NULL;
    }
    for(k = 0; k < G.arcnum; k++){
        // 建立邊表
        v1 = new char[10];
        v2 = new char[10];
        cin >> v1 >> v2 >> w;
        i = LocateVex_ALG(G, v1);
        j = LocateVex_ALG(G, v2);
        edges[k].beginvex = i;
        edges[k].endvex = j;
        edges[k].cost = w;
        p = new ArcNode;
        p->info = NULL;
        p->nextarc = G.vertices[i].firstarc;
        G.vertices[i].firstarc = p;
    }
    Sort(G, edges);  // 按權值大小，對邊進行排序
    for(i = 0; i < G.vexnum; i++)
        parents[i] = 0;
    for(i = 0; i < G.arcnum; i++){
        bnf = Find(parents, edges[i].beginvex);  // 查找邊頭分量
        edf = Find(parents, edges[i].endvex);  // 查找邊尾分量
        if(bnf != edf){
            parents[bnf] = edf;
            cout << edges[i].beginvex << edges[i].endvex;
            cout << " " << edges[i].cost << endl;
        }
    }
}

int Find(int parents[], int f){
    // 查找函數
    while(parents[f] > 0) f = parents[f];
    return f;
}           

Prim和KrusKal比較

算法名 | Prim | KrusKal

時間複雜度 | O(n^2) | O(eloge)

适應範圍 | 稠密圖 | 稀疏圖