前戲
紅黑樹,對很多童鞋來說,是既熟悉又陌生。熟悉是因為在校學習期間,準備面試時,這是重點。然後經過多年的荒廢,如今已經忘記的差不多了。如果正在看文章的你,馬上快要畢業,面臨着找工作的壓力;又或者你覺得需要将這塊知識重新複習一遍;又或者隻是看看,那麼恭喜你,賺到了。那麼我将帶領大家重新認識下紅黑樹,用簡單的語言,搞懂紅黑樹。
在學習紅黑樹之前,咱們需要先來了解下二叉查找樹(BST)。
二叉查找樹
要想了解二叉查找樹,我們首先看下二叉查找樹有哪些特性呢?
1, 左子樹上所有的節點的值均小于或等于他的根節點的值
2, 右子數上所有的節點的值均大于或等于他的根節點的值
3, 左右子樹也一定分别為二叉排序樹
我們來看下圖的這棵樹,他就是典型的二叉查找樹
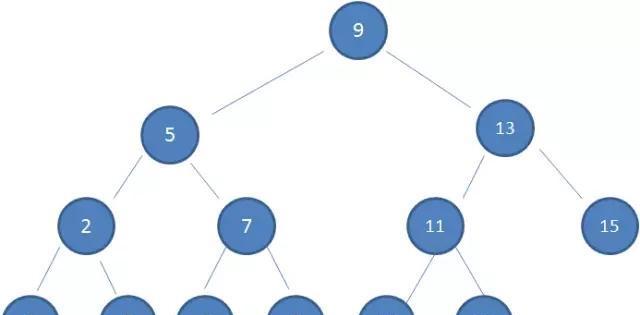
那問題來了,為什麼一定要這種結構呢?換句話說這樣的結構有什麼好處呢?我們就來查找下值為10的節點。它怎麼一步步的找到這個節點的?步驟是怎樣的?接着往下看。
1, 查找到根節點9,看下圖:
2, 由于10大于9的,是以查找到右孩子13,看下圖:
3, 又因為10是小與13的,是以查找到左孩子11,看下圖:
4, 這一步相比不用說了大家也都知道了,找到了左孩子,然後發現正好是10 。恰好是正要尋找的值。
可能又有童鞋會問,這不是二分查找的思想嗎?确實,查找所需的最大次數等同于二叉查找樹的高度。當然在插入節點的時候,也是這種思想,一層一層的找到合适的位置插入。但是二叉查找樹有個比較大的缺陷,而且這個缺陷會影響到他的性能。我們先來看下有一種情況的插入操作:
如果初始的二叉查找樹隻有三個節點,如下圖:
我們依次插入5個節點:7,6,5,4,3,。看下圖插入之後的圖:
看出來了嗎?有沒有覺得很别扭,如果根節點足夠大,那是不是“左腿”會變的特别長,也就是說查找的性能大打折扣,幾乎就是線性查找了。
那有沒有好的辦法解決這個問題呢?解決這種多次插入新節點而導緻的不平衡?這個時候紅黑樹就登場了。
紅黑樹
紅黑樹就是一種平衡的二叉查找樹,說他平衡的意思是他不會變成“瘸子”,左腿特别長或者右腿特别長。除了符合二叉查找樹的特性之外,還具體下列的特性:
1. 節點是紅色或者黑色
2. 根節點是黑色
3. 每個葉子的節點都是黑色的空節點(NULL)
4. 每個紅色節點的兩個子節點都是黑色的。
5. 從任意節點到其每個葉子的所有路徑都包含相同的黑色節點。
看下圖就是一個典型的紅黑樹:
很多童鞋又會驚訝了,天啊這個條條框框也太多了吧。沒錯,正式因為這些規則,才能保證紅黑樹的自平衡。最長路徑不超過最短路徑的2倍。
當插入和删除節點,就會對平衡造成破壞,這時候需要對樹進行調整,進而重新達到平衡。那什麼情況下會破壞紅黑樹的規則呢?
1,我們看下圖:
向原來的紅黑樹插入值為14的新節點,由于父節點15是黑色節點,是以這種情況沒有破壞結構,不需要做任何的改變。
2,向原樹插入21呢?,看下圖:
由于父節點22是紅色節點,是以這種情況打破了紅黑樹的規則4,必須作出調整。那麼究竟該怎麼調整呢?有兩種方式【變色】和【旋轉】分為【左旋轉】和【右旋轉】。
【變色】:
為了符合紅黑樹的規則,會把節點紅變黑或者黑變紅。下圖展示的是紅黑樹的部分,需要注意節點25并非根節點。因為21和22連結出現紅色,不符合規則4,是以把22紅變黑:
但這樣還是不符合規則5,是以需要把25黑變紅,看下圖:
你以為現在結束了?天真,因為25和27又是兩個連續的紅色節點(規則4),是以需要将27紅變黑。
終于結束了,都滿足規則了,舒服多了。
【左旋轉】
也就是逆時針旋轉兩個節點,使父節點被自己的右孩子取代,而自己成為自己的左孩子,聽起來吓死人,直接看圖吧:
【右旋轉】
順時針旋轉兩個節點,使得自己的父節點被左孩子取代,而自己成為自己的右孩子,看不懂直接看圖吧:
看起來這麼複雜,到底怎麼用呢?确實很複雜,我們講下典型的例子,大家參考下:
以剛才插入21節點的例子:
首先我們需要做的是變色,把節點25以及下方的節點變色:
由于17和25是連續的兩個紅色節點,那麼吧節點17變黑嗎?這樣是不行的,你想這樣一來不就打破了規則4了嗎,而且根據規則2,也不可能吧13變成紅色。變色已經無法解決問題了,是以隻能進行旋轉了。13當成X,17當成Y,左旋轉試試看:
由于根節點必須是黑色,是以需要變色,結果如下圖:
繼續,其中有兩條路徑(17-)8->6->NULL)的黑色節點個數不是3,是4不符合規則。
這個時候需要把13當做X,8當做Y,進行右旋轉:
最後根據規則變色:
這樣一來,我們終于結束了,經過調整之後符合規則。
那我們費這麼大力氣,這麼複雜,這東西用在哪裡,有哪些應用呢?
其實STL中的map就是用的紅黑樹。
總結:
紅黑色的大體思想就是上面描述的那樣,裡面還有很多情況要考慮,本文隻是簡單的講述思想,大家有興趣可以去百度上看各種情況的考慮