查找(一)
我們使用符号表這個詞來描寫叙述一張抽象的表格。我們會将資訊(值)存儲在當中,然後依照指定的鍵來搜尋并擷取這些資訊。鍵和值的詳細意義取決于不同的應用。
符号表中可能會儲存非常多鍵和非常多資訊,是以實作一張高效的符号表也是一項非常有挑戰性的任務。
我們會用三種經典的資料類型來實作高效的符号表:二叉查找數、紅黑樹、散清單。
二分查找
我們使用有序數組存儲鍵,經典的二分查找可以依據數組的索引大大降低每次查找所需的比較次數。
在查找時,我們先将被查找的鍵和子數組的中間鍵比較。假設被查找的鍵小于中間鍵,我們就在左子數組中繼續查找。假設大于我們就在右子數組中繼續查找。否則中間鍵就是我們要找的鍵。
普通情況下二分查找都比順序查找快的多,它也是衆多實際應用程式的最佳選擇。對于一個靜态表(不同意插入)來說。将其在初始化時就排序是值得的。
當然,二分查找也不适合非常多應用。現代應用須要同一時候可以支援高效的查找和插入兩種操作的符号表實作。
也就是說,我們須要在構造龐大的符号表的同一時候可以随意插入(或許還有删除)鍵值對,同一時候也要可以完畢查找操作。
要支援高效的插入操作,我們似乎須要一種鍊式結構。當單連結的連結清單是無法使用二分查找的。由于二分查找的高效來自于可以高速通過索引取得不論什麼子數組的中間元素。為了将二分查找的效率和連結清單的靈活性結合起來,我們須要更加複雜的資料結構。
可以同一時候擁有兩者的就是二叉查找樹。
二叉查找樹
一顆二叉查找樹(BST)是一顆二叉樹,當中每一個節點都含有一個可比較的鍵(以及相關聯的值)且每一個結點的鍵都大于其左子樹中的随意結點的鍵而小于右子樹的随意結點的鍵。
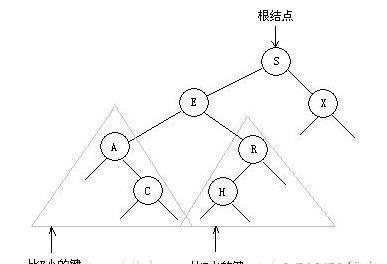
一顆二叉查找樹代表了一組鍵(及其對應的值)的集合。而同一個集合能夠用多顆不同的二叉查找樹表示。
假設我們将一顆二叉查找樹的全部鍵投影到一條直線上,保證一個結點的左子樹中的鍵出如今它的右邊,右子樹中的鍵出如今它的右邊。那麼我們一定能夠得到一條有序的鍵列。
查找
在二叉查找樹中查找一個鍵的遞歸算法:
假設樹是空的。則查找未命中。
假設被查找的鍵和根結點的鍵相等。查找命中。
否則我們就在适當的子樹中繼續查找。假設被查找的鍵較小就選擇左子樹。較大就選擇右子樹。
在二叉查找樹中。随着我們不斷向下查找,目前結點所表示的子樹的大小也在減小(理想情況下是減半)
插入
查找代碼差點兒和二分查找的一樣簡單,這樣的簡潔性是二叉查找樹的重要特性之中的一個。
而二叉查找樹的還有一個更重要的特性就是插入的實作難度和查找差點兒相同。
當查找一個不存在于樹中的結點并結束于一條空連結時,我們須要做的就是将連結指向一個含有被查找的鍵的新結點。假設被查找的鍵小于根結點的鍵。我們會繼續在左子樹中插入該鍵。否則在右子樹中插入該鍵。
分析
使用二叉查找樹的算法的執行時間取決于樹的形狀,而樹的形狀又取決于鍵被插入的先後順序。
在最好的情況下,一顆含有N個結點的樹是全然平衡的。每條空連結和根結點的距離都為~lgN。在最壞的情況下。搜尋路徑上可能有N個結點。但在普通情況下樹的形狀和最好情況更接近。
我們如果鍵的插入順序是随機的。對這個模型的分析而言,二叉查找樹和高速排序差點兒就是“雙胞胎”。樹的根結點就是高速排序中的第一個切分元素(左側的鍵都比它小。右側的鍵都比它大),而這對于全部的子樹相同适用,這和高速排序中對于子數組的遞歸排序全然相應。
【在由N個随機鍵構造的二叉查找樹中,查找命中平均所需的比較次數為~2lgN。 N越大這個公式越準确】
平衡查找樹
在一顆含有N個結點的樹中,我們希望樹高為~lgN。這樣我們就能保證全部查找都能在~lgN此比較内結束,就和二分查找一樣。
不幸的是,在動态插入中保證樹的完美平衡的代價太高了。我們放松對完美平衡的要求,使符号表API中全部操作均可以在對數時間内完畢。
2-3查找樹
為了保證查找樹的平衡性,我們須要一些靈活性。是以在這裡我們同意樹中的一個結點儲存多個鍵。
2-結點:含有一個鍵(及值)和兩條連結。左連結指向的2-3樹中的鍵都小于該結點,右連結指向的2-3樹中的鍵都大于該結點。
3-結點:含有兩個鍵(及值)和三條連結。左連結指向的2-3樹中的鍵都小于該結點,中連結指向的2-3樹中的鍵都位于該結點的兩個鍵之間,右連結指向的2-3樹中的鍵都大于該結點。
(2-3指的是2叉-3叉的意思)
一顆完美平衡的2-3查找樹中的全部空連結到根結點的距離都是同樣的。
要推斷一個鍵是否在樹中,我們先将它和根結點中的鍵比較。
假設它和當中的不論什麼一個相等,查找命中。否則我們就依據比較的結果找到指向對應區間的連結。并在其指向的子樹中遞歸地繼續查找。假設這是個空連結。查找未命中。
要在2-3樹中插入一個新結點,我們可以和二叉查找樹一樣先進行一次未命中的查找。然後把新結點挂在樹的底部。
但這種話樹無法保持完美平衡性。
我們使用2-3樹的主要原因就在于它可以在插入之後繼續保持平衡。
假設未命中的查找結束于一個2-結點,我們僅僅要把這個2-結點替換為一個3-結點,将要插入的鍵儲存在當中就可以。假設未命中的查找結束于一個3-結點,事情就要麻煩一些。
熱身:
先考慮最簡單的樣例:僅僅有一個3-結點的樹。向其插入一個新鍵。
這棵樹唯一的結點中已經沒有可插入的空間了。我們又不能把新鍵插在其空結點上(破壞了完美平衡)。為了将新鍵插入,我們先暫時将新鍵存入該結點中。使之成為一個4-結點。建立一個4-結點非常友善,由于非常easy将它轉換為一顆由3個2-結點組成的2-3樹(如圖所看到的),這棵樹既是一顆含有3個結點的二叉查找樹,同一時候也是一顆完美平衡的2-3樹。當中全部空連結到根結點的距離都相等。
向一個父結點為2-結點的3-結點中插入新鍵
如果未命中的查找結束于一個3-結點。而它的父結點是一個2-結點。
在這樣的情況下我們須要在維持樹的完美平衡的前提下為新鍵騰出空間。
我們先像剛才一樣構造一個暫時的4-結點并将其分解,但此時我們不會為中鍵建立一個新結點。而是将其移動至原來的父結點中。(如圖所看到的)
這次轉換也并不影響(完美平衡的)2-3樹的主要性質。
樹仍然是有序的。由于中鍵被移動到父結點中去了,樹仍然是完美平衡的。插入後全部的空連結到根結點的距離仍然同樣。
向一個父結點為3-結點的3-結點中插入新鍵
如果未命中的查找結束于一個3-結點。而它的父結點是一個3-結點。
我們再次和剛才一樣構造一個暫時的4-結點并分解它,然後将它的中鍵插入它的父結點中。但父結點也是一個3-結點。是以我們再用這個中鍵構造一個新的暫時4-結點,然後在這個結點上進行同樣的變換。即分解這個父結點并将它的中鍵插入到它的父結點中去。
我們就這樣一直向上不斷分解暫時的4-結點并将中鍵插入更高的父結點,直至遇到一個2-結點并将它替換為一個不須要繼續分解的3-結點。或者是到達3-結點的根。
總結:
先找插入結點,若結點有空(即2-結點),則直接插入。如結點沒空(即3-結點),則插入使其暫時容納這個元素,然後分裂此結點。把中間元素移到其父結點中。對父結點亦如此處理。
(中鍵一直往上移。直到找到空位。在此過程中沒有空位就先搞個暫時的,再分裂。
)
★2-3樹插入算法的根本在于這些變換都是局部的:除了相關的結點和連結之外不必改動或者檢查樹的其它部分。每次變換中,變更的連結數量不會超過一個非常小的常數。全部局部變換都不會影響整棵樹的有序性和平衡性。
{你确定了解了2-3樹的插入過程了嗎? 假設你了解了,那麼你也就基本了解了紅黑樹的插入}
構造
和标準的二叉查找樹由上向下生長不同,2-3樹的生長是由下向上的。
長處
2-3樹在最壞情況下仍有較好的性能。每一個操作中處理每一個結點的時間都不會超過一個非常小的常數,且這兩個操作都僅僅會訪問一條路徑上的結點,是以不論什麼查找或者插入的成本都肯定不會超過對數級别。
完美平衡的2-3樹要平展的多。比如,含有10億個結點的一顆2-3樹的高度僅在19到30之間。我們最多僅僅須要訪問30個結點就能在10億個鍵中進行随意查找和插入操作。
缺點
我們須要維護兩種不同類型的結點,查找和插入操作的實作須要大量的代碼。并且它們所産生的額外開銷可能會使算法比标準的二叉查找樹更慢。
平衡一棵樹的初衷是為了消除最壞情況,但我們希望這樣的保障所需的代碼可以越少越好。
紅黑二叉查找樹
【前言:本文所讨論的紅黑樹之目的在于使讀者能更簡單清晰地了解紅黑樹的構造,使讀者能在紙上清晰高速地畫出紅黑樹。而不是為了寫出紅黑樹的實作代碼。
若是要在代碼級了解紅黑樹。則勢必須要記住其複雜的插入和旋轉的各種情況。我覺得那僅僅有助于添加大家對紅黑樹的恐懼,實際面試和工作中差點兒不會遇到須要自己動手實作紅黑樹的情況(非常多語言的标準庫中就有紅黑樹的實作)。 若對于紅黑樹的C代碼實作有興趣的,可移步至July的部落格。
】
(了解紅黑樹一句話就夠了:紅黑樹就是用紅連結表示3-結點的2-3樹。那麼紅黑樹的插入、構造就可轉化為2-3樹的問題,即:在腦中用2-3樹來操作,得到結果。再把結果中的3-結點轉化為紅連結就可以。而2-3樹的插入。前面已有具體圖文,實際也非常easy:有空則插,沒空硬插,再分裂。 這樣,我們就不用記那麼複雜且讓人頭疼的紅黑樹插入旋轉的各種情況了。
僅僅要清楚2-3樹的插入方式就可以。 以下圖文具體示範。)
紅黑樹的本質:
紅黑樹是對2-3查找樹的改進,它能用一種統一的方式完畢全部變換。
替換3-結點
★紅黑樹背後的思想是用标準的二叉查找樹(全然由2-結點構成)和一些額外的資訊(替換3-結點)來表示2-3樹。
我們将樹中的連結分為兩種類型:紅連結将兩個2-結點連接配接起來構成一個3-結點,黑連結則是2-3樹中的普通連結。确切地說。我們将3-結點表示為由一條左斜的紅色連結相連的兩個2-結點。
這樣的表示法的一個長處是,我們無需改動就能夠直接使用标準二叉查找樹的get()方法。對于随意的2-3樹,僅僅要對結點進行轉換。我們都能夠馬上派生出一顆相應的二叉查找樹。
我們将用這樣的方式表示2-3樹的二叉查找樹稱為紅黑樹。
紅黑樹的還有一種定義是滿足下列條件的二叉查找樹:
⑴紅連結均為左連結。
⑵沒有不論什麼一個結點同一時候和兩條紅連結相連。
⑶該樹是完美黑色平衡的。即随意空連結到根結點的路徑上的黑連結數量同樣。
假設我們将一顆紅黑樹中的紅連結畫平,那麼全部的空連結到根結點的距離都将是同樣的。
假設我們将由紅連結相連的結點合并,得到的就是一顆2-3樹。
相反,假設将一顆2-3樹中的3-結點畫作由紅色左連結相連的兩個2-結點,那麼不會存在可以和兩條紅連結相連的結點。且樹必定是完美平衡的。
不管我們用何種方式去定義它們,紅黑樹都既是二叉查找樹。也是2-3樹。
(2-3樹的深度非常小,平衡性好。效率高,可是其有兩種不同的結點,實際代碼實作比較複雜。而紅黑樹用紅連結表示2-3樹中另類的3-結點,統一了樹中的結點類型。使代碼實作簡單化,又不破壞其高效性。
顔色表示:
由于每一個結點都僅僅會有一條指向自己的連結(從它的父結點指向它),我們将連結的顔色儲存在表示結點的Node資料類型的布爾變量color中(若指向它的連結是紅色的,那麼該變量為true,黑色則為false)。
當我們提到一個結點顔色時,我們指的是指向該結點的連結的顔色。
旋轉
在我們實作的某些操作中可能會出現紅色右連結或者兩條連續的紅連結,但在操作完畢前這些情況都會被小心地旋轉并修複。
(我們在這裡不讨論旋轉的幾種情況,把紅黑樹看做2-3樹,自然能夠得到正确的旋轉後結果)
在插入時我們能夠使用旋轉操作幫助我們保證2-3樹和紅黑樹之間的一一相應關系,由于旋轉操作能夠保持紅黑樹的兩個重要性質:有序性和完美平衡性。
向2-結點中插入新鍵
(向紅黑樹中插入操作時,想想2-3樹的插入操作。紅黑樹與2-3樹在本質上是同樣的,僅僅是它們對3結點的表示不同。
向一個僅僅含有一個2-結點的2-3樹中插入新鍵後,2-結點變為3-結點。
我們再把這個3-結點轉化為紅結點就可以)
向一顆雙鍵樹(即一個3-結點)中插入新鍵
(向紅黑樹中插入操作時,想想2-3樹的插入操作。你把紅黑樹當做2-3樹來處理插入。一切都變得簡單了)
(向2-3樹中的一個3-結點插入新鍵。這個3結點暫時成為4-結點,然後分裂成3個2結點)
★一顆紅黑樹的構造全過程
平衡二叉樹(AVL樹)
定義:平衡二叉樹(Balance Binary Tree)又稱AVL樹。它或者是一顆空樹,或者是具有下列性質的二叉樹:它的左子樹和右子樹都是平衡二叉樹。且左子樹和右子樹的深度之差的絕對值不超過1。
若将二叉樹上結點的平衡因子BF(BalanceFactor)定義為該結點的左子樹深度減去它的右子樹深度。則平衡因子的絕對值大于1。
其旋轉操作 用2-3樹的分裂來類比想象。
下半部分——散清單、B樹、B+樹、Trie樹。