紅黑樹是一種二叉搜尋樹,單次操作複雜度上限$logn$,效率極高,基本用指針實作。
為了減小常數,紅黑樹的操作全部非遞歸實作。
下面系統介紹一下紅黑樹,包括複雜度的證明和基本操作。
1、紅黑樹的結構:
紅黑樹是二叉搜尋樹,滿足BST性質,左兒子數值都小于目前節點,右兒子數值都大于目前節點,中序周遊單調遞增。
紅黑樹根節點的父親和葉節點的兒子指向同一個節點,稱為紅黑樹的葉節點。
葉節點不僅具有哨兵的作用,也可以減少情況,簡化代碼,哨兵可以當作普通的黑色節點。
葉節點以外得點被稱為紅黑樹的内節點。
每個節點有六個域,分别為$key$,$si$,$we$,$co$,$f$和$ch$,$key$代表目前點的權值,$we$代表目前值的個數,$si$代表子樹大小,$ch$代表左右兒子,$f$代表父親,$co$代表目前節點的顔色。
設$bh(x)$為節點$x$到葉節點的一條路徑上的黑色節點數目,稱為該節點的黑高,紅黑樹的黑高為根節點的黑高。
設$h(x)$為節點$x$到葉節點的所有路徑中最長的一條的長度。
設$rt$代表紅黑樹的根。
一顆完整的紅黑樹如下圖:
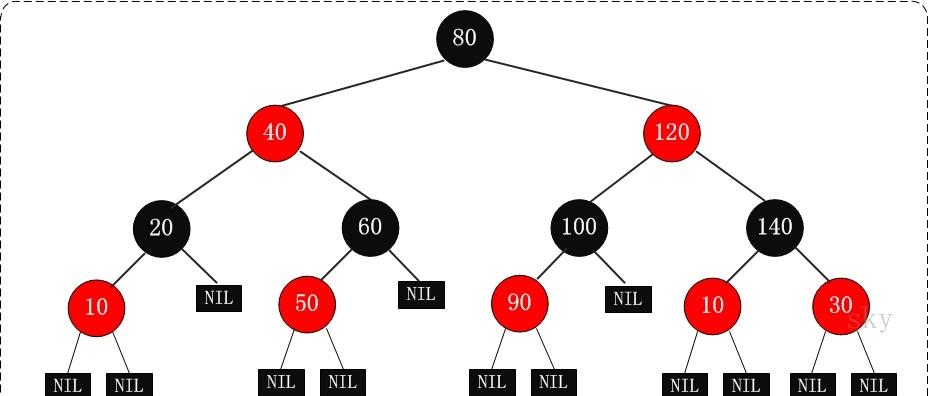
2、紅黑樹的性質:
一顆完整的紅黑樹具有以下性質:
1、每個節點都是紅色或黑色;
2、根節點和葉節點是黑色;
3、紅色節點的兒子都是黑色;
4、從根節點到葉節點的每條路徑上經過的黑色節點數相同。
這些性質保證了紅黑樹的優秀複雜度。
3、紅黑樹複雜度的證明:
我們要證明紅黑樹的時間複雜度為$O(logn)$。
引理一:紅黑樹中沒有任何一條從根節點到葉節點的路徑比另一條長出一倍。
證明:
從每個節點到葉子的路徑上的黑色節點數稱為該節點的黑高度,記為$bh$。
根據性質4,根節點到葉節點的每條路徑上黑色節點數相同;再根據性質3,紅色節點的兒子都是黑色。
把根節點到葉節點的路徑看成一個序列,把紅色節點插入到黑色節點之間,則沒有兩個紅色節點相鄰。
是以一條路徑上紅色節點數不會超過黑色節點數,沒有任何一條路徑比另一條長出一倍。
證畢。
引理二:以$x$為根的子樹中至少包含$2^{hb(x)}-1$個内節點。
用數學歸納法證明。
如果$hb(x)=0$,$x$一定是葉節點,結論顯然成立。
對于其他節點,每個節點都有兩個兒子,根據兒子的顔色,每個兒子的黑高為$hb(x)$或$hb(x)-1$,并且兒子節點的黑高都小于目前節點的黑高。
根據前一布的歸納可以得出,以兒子節點為根的子樹内至少有$2^{hb(x)-1}-1$個節點。
是以最次情況下,即兩個兒子的黑高都是$hb(x)-1$的情況下,目前子樹大小可以去得最小值$2^{hb(x)}-1$,其餘情況下均大于這個值。
引理三:一顆含有$n$個節點的紅黑樹,高度至多為$2log(n+1)$。
根據性質3和性質4,從根到葉節點的其中一條簡單路徑上黑色節點占一半以上。
是以$hb(x)>=\frac{h(x)}{2}$,當$x$為根時,根據引理二,可以得到不等式:
$n>=2^{\frac{h}{2}}-1$
移項後取對數可得:
$h<=2lg(n+1)$
4、旋轉:
旋轉是紅黑樹的必要操作。
紅黑樹的旋轉和其他的帶旋平衡樹類似,會帶旋treap,splay,AVL或SBT的大佬可以選擇跳過。
旋轉分為左旋和右旋,都是在維護BST性質下對樹的結構進行的局部調整。
記住是局部調整,對紅黑樹的其他位置都沒有影響。
定義$rotate(x,p)$表示以$x$的父親為支點左/右旋,0代表右旋,1代表左旋。
一張圖了解一下:
旋轉要保證$x$和$y$均不為空(均不是哨兵),對于$\alpha$,$\beta$和$\gamma$則沒有特殊要求。
以0代表左兒子,以1代表右兒子,就是$p^1$兒子過繼給父親,原來的祖父變為父親,原來的父親變為兒子。
左旋和右旋改變的僅有父指針和兒子指針,以及pushup時更新的子樹大小,節點的其他域都沒有改變。
經過旋轉,可以調節紅黑樹的整體結構,使其更加平衡。
代碼如下:
void rotate(node *now,int pos){//旋轉操作
node *c=now->ch[pos^1];
now->ch[pos^1]=c->ch[pos];
if(c->ch[pos]->si) c->ch[pos]->f=now;
c->f=now->f;
if(!now->f->si) rt=c;//旋到根
else now->f->ch[now->f->ch[0]!=now]=c;
c->ch[pos]=now;now->f=c;c->si=now->si;
now->pushup();//更新子樹大小
} 旋轉
左旋和右旋的時間複雜度為$O(1)$但常數極大,制約了平衡樹的效率。
而紅黑樹通過紅黑染色,減少旋轉的次數,使得每次旋轉的次數不超過$\frac{2}{3}logn$,$n$為目前的紅黑樹大小,極大地優化了常數,這也是紅黑樹效率高的原因。
5、紅黑樹的查詢
由于紅黑樹的插入和删除非常繁瑣,我們在這裡先讨論查詢操作。
紅黑樹僅在插入和删除時會有結構的調整,其他情況下結構是固定的,可以和BST一樣直接查詢。
由于滿足BST性質,所有查詢都是從根開始。
1、查某個數$val$的排名:
如果目前節點權值大于$val$,查詢左兒子即可;
如果目前節點權值小于$val$,把右子樹大小和目前節點大小累加進答案,然後查詢右兒子;
如果目前節點權值等于$val$,結束查詢,答案加$1$(因為此時的答案為小于$val$的數的個數)。
2、查詢排名為$rnk$的數:
如果目前節點左子樹大小大于$rnk$,查詢左兒子;
如果目前節點左子樹大小和目前節點大小之和小于$rnk$,查詢右兒子;
其餘情況下結束查詢,傳回目前節點權值。
3、查找某一個數$val$:
如果目前節點權值大于$val$,查詢左兒子;
如果目前節點權值小于$val$,查詢右兒子;
如果目前節點權值等于$val$,結束查詢,傳回目前節點。
4、查詢值$val$的前驅:
如果目前節點權值小于$val$,用目前點權值更新答案(取$max$),查詢右兒子;
如果目前節點權值等于$val$,結束查詢,傳回答案。
5、查詢值$val$的後繼:
初始化答案為$inf$。
如果目前節點權值大于$val$,用目前點權值更新答案(取$minx$),查詢左兒子;
node *find(reg node *now,int key){//查找位置
for(;now->si&&now->key!=key;now=now->ch[now->key<key]);
return now;
}
int rnk(int key){//查排名
reg int res,ans=0;
for(reg node *now=rt;now->si;){
res=now->ch[0]->si;
if(now->key==key) break;
else if(now->key>key) now=now->ch[0];
else{
ans+=res+now->we;now=now->ch[1];
}
}
return ans+res+1;
}
int kth(int k){//查數
reg int res;reg node *now=rt;
for(;now->si;){
res=now->ch[0]->si;
if(k<=res) now=now->ch[0];
else if(res+1<=k&&k<=res+now->we) break;
else{
k-=res+now->we;now=now->ch[1];
}
}
return now->key;
}
int pre(int key){//前驅
reg int res=0;
for(reg node *now=rt;now->si;){
if(now->key<key){
res=now->key;now=now->ch[1];
}
else now=now->ch[0];
}
return res;
}
int nxt(int key){//後繼
reg int res=0;
for(reg node *now=rt;now->si;){
if(now->key>key){
res=now->key;now=now->ch[0];
}
else now=now->ch[1];
}
return res;
} 查詢
6、紅黑樹的插入:
如果樹中有對應權值,那麼問題很簡單,找到對應權值,将路徑上的節點$si$加一即可。
但是對于其他情況如何處理。
插入時會影響到紅黑樹的整體結構,破壞紅黑樹的性質。
為了維持優秀的複雜度及常數,我們需要對插入進行修正。
在插入的同時維護紅黑樹的性質并不簡單,我們可以先找到一個位置,将新節點插進去,再對樹進行調整。
插入代碼如下:
inline void insert(int key){//插入節點
reg node *now=rt,*fa=nul;int pos;
for(;now->si;now=now->ch[pos]){
now->si++;fa=now;
pos=now->getpos(key);
if(pos==-1){//找到對應值
now->we++;return;
}
}
now=New(key);//找到位置,插入節點
if(fa->si) fa->ch[key>fa->key]=now;
else rt=now;
now->f=fa;insert_transfrom(now);
} 插入
然後我們就可以進行繁瑣的修正過程了。
首先對節點有如下定義:
其中,$fa$代表父親,$gr$代表祖父,$un$代表叔叔,$br$代表兄弟。
插入的新節點要染一個顔色,那麼染什麼顔色好呢。
由于我們并不知道樹的具體形态和着色方案,是以染紅色或黑色都有可能破壞樹的結構和性質。
我們可以發現,染成黑色可能破壞性質4,染成紅色可能破壞性質3和2,然而可以發現性質3的修正比較容易,是以建立節點染成紅色。
我們需要一個疊代過程進行修正。
疊代的過程中要維持性質4不被破壞,并且破壞性質2和3的點不超過一個,不然我們的操作就沒有意義了。
初始時最多有一個不滿足性質的節點,也就是新插入的節點,每次修正都會修正目前節點,并産生至多一個新的不滿足性質3的節點。而且這個節點的深度一定小于之前的點,是以紅黑樹修正的時間複雜度為$O(logn)$。
可以發現因為破壞性質2和3都需要該點為紅色,而破壞性質3還需要父親為紅色。
如果破壞性質2,那麼該點一定為根節點,直接染黑即可。
其餘情況下,如果父親為黑色,一定滿足性質,疊代到達終點。而父親是紅色時,也就是需要調整時,祖父一定是黑色。
情況一:叔叔為紅色。
解決方法:将父親和祖父染黑,祖父染紅,繼續處理祖父。
不難發現,紅黑樹的性質3得到修正,并且性質4沒有破壞。
如圖所示:
情況二:叔叔為黑色,且目前點,父親和祖父不共線。
解決方法:以父親為支點向目前點的反方向旋轉,繼續處理原父親。
這樣可以在維持性質的同時轉化為情況三。