引用與前言
參考連結
引用參考如下:
- 部落格園解釋:javascript:void(0) 這篇部落格園寫的賊棒!我當時就是一邊對着論文一邊對着他這篇來看的,是以大部分論文的文字也來源于此
- 原文論文:https://ieeexplore.ieee.org/document/580977 沒有賬号的話 就去sci-hub吧,這裡是preprint版:colli.dvi (cmu.edu)
-
Python代碼:https://github.com/AtsushiSakai/PythonRobotics
ROS代碼:http://wiki.ros.org/dwa_local_planner
前言/基礎知識
其實這篇我大學畢業論文用到了 當時很仔細的看過一遍,但是因為沒有對着代碼看,僅看了一下論文的數學公式推導等,就覺得很厲害,想到這樣的方式去表示和限制。這次專門複習再來一次 結合着代碼看一次好了。這次直接使用Typro打的markdown檔案,這樣在部落格園的格式應該很好看了,目錄也是在左邊~
首先,我們要了解這個幹什麼的,在路徑規劃算法 主要包括全局路徑規劃和局部路徑規劃。局部路徑規劃主要用于動态環境下的導航和避障,對于無法預測的障礙物DWA算法可以較好地解決。DWA算法的優點是計算負複雜度較低,由于考慮到速度和加速度的限制,隻有安全的軌迹會被考慮,且每次采樣的時間較短,是以軌迹空間較小。采樣的速度即形成了一個動态視窗
直接跳轉可以先看看運作的效果,感受一下
論文部分
介紹/Introduction
DWA的整體軌迹評價函數主要是三個方面:
- 與目标的接近程度
- 機器人前進的速度
- 與下一個障礙物的距離
簡而言之就是在局部規劃出一條路徑,希望與目标越來越近,且速度較快,與障礙物盡可能遠。評價函數權衡以上三個部分得到一條最優路徑。
該論文相對于之前的創新點在于:
- 該方法是由一個移動機器人的運動動力學推導出來的
- 考慮到機器人的慣性(代碼中計算了刹車距離),這對于具有扭矩限制機器人在高速行駛時很重要。
- 在動态雜亂環境中速度可以較快,對于速度較快的機器人以及低電動機轉矩的機器人較為實用。
相關工作/Related Work
這部分對比的時候,因為年代的原因是随着全局規劃一起對比的
- 全局優點在于計算時可以離線進行,但是目前ROS中全局路徑也在導航過程中不斷變化。
- 全局缺點在于不能适應環境變化以及計算複雜度太高,尤其是環境不斷變化時。
- 局部缺點在于不能保證得到最優解,容易陷入局部最優(如U形障礙環境)。
- 局部優點在于計算速度快,适合環境不斷變化。
- 對比了其他的局部路徑規劃算法的優缺點:勢場法計算速度很快,但是在狹窄區域會産生震蕩,如果目标點在兩個很近的障礙物之間,則可能找不到路徑。
機器人運動學方程
為了使運動學方程更加接近實際,将模型的速度設為随時間變化的分段函數,在該假設下,機器人軌迹可看做許多的圓弧積分組成,采用該方法使得障礙物碰撞檢測很友善,因為圓弧與障礙物的交點很好求。
其中關于公式參數的提前解釋:
- \(x(t)\), \(y(t)\), \(\theta(t)\) 分别表示機器人在 \(t\) 時刻的\(x\) 坐标、\(y\) 坐标以及朝向角
- \(x(t_0)\), \(x(t_n)\) 分别表示機器人在 \(t_0\) 和 \(t_1\) 時刻的\(x\)坐标
- \(v(t)\) 表示機器人的平移速度
\[x\left(t_{n}\right)=x\left(t_{0}\right)+\int_{t_{0}}^{t_{n}} v(t) \cdot \cos \theta(t) d t \tag{1}
\]
\[y\left(t_{n}\right)=y\left(t_{0}\right)+\int_{t_{0}}^{t_{n}} v(t) \cdot \sin \theta(t) d t \tag{2}
由此得知坐标是根據速度來得到的,而這個速度不能說直接給他設定,有限制的。例如,機器人速度 \(v(t)\) 取決于初始時刻 \(t_0\) 的速度和時間 \(t_0\),和速度一樣的, \(\theta(t)\) 也是初始轉向角 \(\theta(t_0)\) 函數
- 機器人在時間間隔 \(\hat t \in [t_0,t]\) 的平移加速度為 \(\dot v(\hat t)\)
- \(t_0\) 時刻的初始旋轉速度為 \(w(t_0)\),\(\hat t \in [t_0,t]\) 的旋轉加速度為 \(\dot w(\hat t)\),故(1)可以轉為:
\[x\left(t_{n}\right)=x\left(t_{0}\right)+\int_{t_{0}}^{t_{n}}\left(v\left(t_{0}\right)+\int_{t_{0}}^{t} \dot{v}(\hat{t}) d \hat{t}\right) \cdot \cos \left(\theta\left(t_{0}\right)+\int_{t_{0}}^{t}\left(\left(w\left(t_{0}\right)+\int_{t_{0}}^{\bar{t}} \dot{w}(\tilde{t}) d \tilde{t}\right) d \tilde{t}\right) d t\right. \tag{3}
此時機器人的軌迹由初始時刻的狀态以及加速度決定,可以認為這些狀态是可控的,同時由于機器人内部結構原因,其加速度也不是一直變化(類似于連續函數),是以可以将 \(t_0\) 到 \(t_n\) 看作是很多個時間片,積分可以轉換為求和,假設有\(n\)個時間片,在每個\([t_i,t_{i+1}]\),機器人的加速度 \(\dot v_i\)和\(\dot w\) 保持不變,設\(\Delta^i_t=t-t_i\),那麼(3) 又可以再一步:
\[x\left(t_{n}\right)=x\left(t_{0}\right)+\sum_{i=0}^{n-1} \int_{t_{i}}^{t_{i+1}}\left(v\left(t_{i}\right)+\dot{v}_{i} \cdot \Delta_{t}^{i}\right) \cdot \cos \left(\theta\left(t_{i}\right)+w\left(t_{i}\right) \cdot \Delta_{t}^{i}+\frac{1}{2} \dot{w}_{i} \cdot\left(\Delta_{t}^{i}\right)^{2}\right) d t \tag{4}
式(4)雖然與機器人的動力控制相關,但是不能決定機器人具體的駕駛方向,對于障礙物與機器人軌迹的交點也很難求出,可以繼續進行簡化,既然時間間隔很小,那麼我們就把,那麼就可以得到(5)
- \(v(t_i)+\dot v_i \cdot \Delta^i_t\) 近似為 \(v_i \in [v(t_i),v(t_{i+1})]\)
- \(\theta\left(t_{i}\right)+w\left(t_{i}\right) \cdot \Delta_{t}^{i}+\frac{1}{2} \dot{w}_{i} \cdot\left(\Delta_{t}^{i}\right)^{2}\) 近似為 \(\theta\left(t_{i}\right)+w\left(t_{i}\right) \cdot \Delta_{t}^{i}\)
\[x\left(t_{n}\right)=x\left(t_{0}\right)+\sum_{i=0}^{n-1} \int_{t_{i}}^{t_{i+1}} v_{i} \cdot \cos \left(\theta\left(t_{i}\right)+w_{i} *\left(\hat{t}-t_{i}\right)\right) d \hat{t} \tag{5}
最後解這個積分方程,簡化為:
\[x\left(t_{n}\right)=x\left(t_{0}\right)+\sum_{i=0}^{n-1} F^i_x(t_{i+1}) \tag{6}
其中\(F\) 展開就是:
\[F_{x}^{i}\left(t_{i}\right)=\left\{\begin{array}{l}
\frac{v_{i}}{w_{i}}\left(\sin \theta\left(t_{i}\right)-\sin \left(\theta\left(t_{i}\right)+w_{i} \cdot\left(t-t_{i}\right)\right)\right), w_{i} \neq 0 \\
v_{i} \cos \left(\theta\left(t_{i}\right)\right) \cdot t, w_{i}=0
\end{array}\right. \tag{7}
以上都是推導\(x\) 坐标,對于\(y\) 整個過程也是一樣的,就是\(F\) 裡面的一個三角函數變換了
\[y\left(t_{n}\right)=y\left(t_{0}\right)+\sum_{i=0}^{n-1} F^i_y(t_{i+1}) \tag{8}
\[F_{y}^{i}\left(t_{i}\right)=\left\{\begin{array}{l}
-\frac{v_{i}}{w_{i}}\left(\cos \theta\left(t_{i}\right)-\cos \left(\theta\left(t_{i}\right)+w_{i} \cdot\left(t-t_{i}\right)\right)\right), w_{i} \neq 0 \\
v_{i} \sin \left(\theta\left(t_{i}\right)\right) \cdot t, w_{i}=0
\end{array}\right. \tag{9}
- 當\(w_i=0\) 時,機器人行走軌迹為一條直線
-
當\(w_i \not = 0\) 時,機器人軌迹為圓弧,設:
\[M_{x}^{i}=-\frac{v_{i}}{w_{i}} \cdot \sin \theta\left(t_{i}\right) \tag{10}
\[M_{y}^{i}=\frac{v_{i}}{w_{i}} \cdot \cos \theta(t-i) \tag{11}
然後,奇妙的事情就發生了,我們可以得到這樣一個式子:
\[\left(F_{x}^{i}-M_{x}^{i}\right)^{2}+\left(F_{x}^{i}-M_{x}^{i}\right)^{2}=\left(\frac{v_{i}}{w_{i}}\right)^{2} \tag{12}
這個式子就是圓在平面的公式,其中這個圓的圓心為 \((M^i_x,M^i_y)\),半徑為\(\frac{v_i}{w_i}\)。根據上述公式可以求出機器人的軌迹,即通過一系列分段的圓弧和直線來拟合軌迹。
誤差界
将機器人軌迹進行分段會在控制點之間産生線性誤差,即\(t_{i+1}−t_i\)之間的誤差,設x坐标和y坐标的誤差分别為\(E^i_x\)和\(E^i_y\),\(\Delta t_i=t_{i+1}−t_i\),由于\(i∈[v(t_i),v(t_{i+1})]\),故最大誤差\(E^i_x,E^i_y≤|v(t_{i+1})−v(t_i)|\cdot \Delta t_i\),在\(\Delta t_i\)内是線性的。注意該上界誤差僅僅可用于機器人内部預測,而實際機器人位置一般通過裡程計測量。
動态視窗法
動态視窗法在速度空間中進行速度采樣,并對随機采樣的速度進行限制,減小采樣數目,在使用代價函數進行評價。
1. 速度搜尋空間
根據以下三點進行速度空間降采樣
- 圓弧軌迹:動态視窗法僅僅考慮圓弧軌迹,該軌迹由采樣速度 \((v,w)\) 決定,這些速度構成一個速度搜尋空間。
- 允許速度:如果機器人能夠在碰到最近的障礙物之前停止,則該采樣速度将被評估。
- 動态視窗:由于機器人加速度的限制,是以隻有在加速時間内能達到的速度才會被保留。
2. 最優化
代價函數方程:
\[G(v,w)=\sigma(\alpha \cdot \text{heading}(v,w)+\beta \cdot \text{dist}(v,w) + \gamma \cdot \text{vel}(v,w)) \tag{13}
最大值即使最優值最大,其中\(\sigma\)使得三個部分的權重更加平滑,使得軌迹與障礙物之間保持一定的間隙。
- Target heading: heading用于評價機器人與目标位置的夾角,當機器人朝着目标前進時,該值取最大;舉個例子:表示機器人與目标點的對齊程度,用\(180−θ\)表示,\(θ\)為機器人與目标夾角,夾角越大,代價值越小。
【路徑規劃】 The Dynamic Window Approach to Collision Avoidance (附python代碼執行個體) - Clearance: dist 用于表示與機器人軌迹相交的最近的障礙物距離;如果障礙物與機器人軌迹不相交,則設為一個較大的值
- Velocity: vel 表示機器人的前向移動速度,支援快速移動
安全速度
機器人能夠在撞掉障礙物之前停下,\(\text{dist}(v,w)\) 為機器人軌迹上與障礙物的最近距離,設刹車時的加速度為 \(\dot v_b, \dot w_b\) ,則 \(V_a\) 為機器人不與障礙物碰撞的速度集合:
\[V_{a}=\left\{v, w \mid v \leq \sqrt{2 \cdot \text{dist}(v, w) \cdot \dot{v}_{b}} \cap w \leq \sqrt{2 * \text{dist}(v, w) * \dot{w}_{b}}\right\}
動态視窗速度
考慮到機器人的動力加速度,搜尋空間降采樣到動态視窗,隻保留以目前加速度可到達的速度,設\(t\)為時間間隔,\((v_a,w_a)\)為實際速度,則動态視窗的速度集合為\(V_d\):該集合以外的速度都不能在該時間間隔内達到。
\[V_{d}=\left\{v, w \mid v \in\left[v_{a}-\dot{v} \cdot t, v_{a}+\dot{v} \cdot t\right] \cap w \in\left[w_{a}-\dot{w} \cdot t, w_{a}+\dot{w} \cdot t\right]\right\}
綜上,最終的搜尋空間:
\[V_{r}=V_{s} \cap V_{a} \cap V_{d}
最終的代價函數的限制就是在這個搜尋空間内的
實驗部分
平滑處理:
評價函數的三個部分都被正則化在\([0,1]\)上,實驗中設定了\(α=2\),\(β=0.2\),\(γ=0.2\),平滑處理可以使機器人與障礙物之間有一定的間隙(裕度)。
實作細節:
- 當機器人陷入局部最優時(即不存在路徑可以通過),使其原地旋轉,直到找到可行路徑。
- 安全裕度:在路徑規劃時,設定一安全裕度,即在路徑和障礙物之間保留一定間隙,且該間隙随着速度增大線性增長。
參數設定:
- \(α\) 占比重太大,機器人運動自由度大,窄的區域不容易通過,\(α\)占比重太小,機器人軌迹則不夠平滑。是以\(α\) 越大,越适合在窄區域,\(α\) 越小,越适合在寬區域。
代碼部分
這裡先說一下整體的思路,主要是對着參考的Python代碼的,有空我把ROS_wiki那邊也補充完整
- 設定初始狀态:\([x,y,\theta,v,\omega]\) ;目标位置:\([x_{goal},y_{goal}]\)
- 機器人的參數:最大最小速度、最大轉角(偏航角)速度、最大加速度、最大角加速度、速度和偏航角分辨率、預測時間範圍(就是生成多大的空間)、目标,速度,障礙物的各個cost設定、各個障礙物的位置
- 計算動态視窗
- 計算控制和軌迹點
1. 計算動态視窗
主要是根據現在的狀态和預設的參數進行的設定:
def calc_dynamic_window(x, config):
"""
calculation dynamic window based on current state x
"""
# Dynamic window from robot specification
Vs = [config.min_speed, config.max_speed,
-config.max_yaw_rate, config.max_yaw_rate]
# Dynamic window from motion model
Vd = [x[3] - config.max_accel * config.dt,
x[3] + config.max_accel * config.dt,
x[4] - config.max_delta_yaw_rate * config.dt,
x[4] + config.max_delta_yaw_rate * config.dt]
# [v_min, v_max, yaw_rate_min, yaw_rate_max]
dw = [max(Vs[0], Vd[0]), min(Vs[1], Vd[1]),
max(Vs[2], Vd[2]), min(Vs[3], Vd[3])]
return dw
可以從中看出 主要是速度的整個視窗,讀取機器人的預設速度配置,然後計算加速度時間後的速度取最小最大的,形成一個取速度的範圍
2. 采樣軌迹
根據現在的狀态和前面的速度動态視窗,配置中的速度分辨率(就是以多少間隔生成速度值)
# evaluate all trajectory with sampled input in dynamic window
# for v in np.arange(dw[0], dw[1], config.v_resolution):
# for y in np.arange(dw[2], dw[3], config.yaw_rate_resolution):
# trajectory = predict_trajectory(x_init, v, y, config)
def predict_trajectory(x_init, v, y, config):
"""
predict trajectory with an input
"""
x = np.array(x_init)
trajectory = np.array(x)
time = 0
while time <= config.predict_time:
x = motion(x, [v, y], config.dt)
trajectory = np.vstack((trajectory, x))
time += config.dt
return trajectory
其中motion就是由車輛運動的模型得出來的這時刻狀态加速度得到下一時刻的狀态,根據前面可知:
v
是速度,
y
是yaw角速度,
x
的各個位置為:\([x,y,\theta,v,\omega]\)
def motion(x, u, dt):
"""
motion model
"""
x[2] += u[1] * dt # v=v+a*t
x[0] += u[0] * math.cos(x[2]) * dt # x=x+v*cos(theta)
x[1] += u[0] * math.sin(x[2]) * dt # y=y+v*sin(theta)
x[3] = u[0]
x[4] = u[1]
return x
3. 計算cost
goal cost
這個cost也就是前面最優化裡面提到的heading cost,朝向
def calc_to_goal_cost(trajectory, goal):
"""
calc to goal cost with angle difference
"""
dx = goal[0] - trajectory[-1, 0]
dy = goal[1] - trajectory[-1, 1]
error_angle = math.atan2(dy, dx)
cost_angle = error_angle - trajectory[-1, 2]
cost = abs(math.atan2(math.sin(cost_angle), math.cos(cost_angle)))
return cost
速度cost
速度cost之間是根據得出的軌迹的速度和最大速度做個內插補點再乘一個速度cost的系數得出來的
speed_cost = config.speed_cost_gain * (config.max_speed - trajectory[-1, 3])
障礙物cost
這麼一看 果然還是圓形比較适合做碰撞檢測,怪不得傑哥中間也是将車膨脹成兩個圓
def calc_obstacle_cost(trajectory, ob, config):
"""
calc obstacle cost inf: collision
"""
ox = ob[:, 0]
oy = ob[:, 1]
dx = trajectory[:, 0] - ox[:, None]
dy = trajectory[:, 1] - oy[:, None]
r = np.hypot(dx, dy)
if config.robot_type == RobotType.rectangle:
yaw = trajectory[:, 2]
rot = np.array([[np.cos(yaw), -np.sin(yaw)], [np.sin(yaw), np.cos(yaw)]])
rot = np.transpose(rot, [2, 0, 1])
local_ob = ob[:, None] - trajectory[:, 0:2]
local_ob = local_ob.reshape(-1, local_ob.shape[-1])
local_ob = np.array([local_ob @ x for x in rot])
local_ob = local_ob.reshape(-1, local_ob.shape[-1])
upper_check = local_ob[:, 0] <= config.robot_length / 2
right_check = local_ob[:, 1] <= config.robot_width / 2
bottom_check = local_ob[:, 0] >= -config.robot_length / 2
left_check = local_ob[:, 1] >= -config.robot_width / 2
if (np.logical_and(np.logical_and(upper_check, right_check),
np.logical_and(bottom_check, left_check))).any():
return float("Inf")
elif config.robot_type == RobotType.circle:
if np.array(r <= config.robot_radius).any():
return float("Inf")
min_r = np.min(r)
return 1.0 / min_r # OK
這一步直接計算了所有的障礙物的,也得益于python的友善,直接計算軌迹與各個障礙物的直線距離,判斷是否對于圓半徑,隻要有一個障礙物碰到了 這條軌迹就被抛棄了,如果沒有的話 輸出最小的那個距離,然後分之一進行輸出以便計算cost
綜合下來就是:
# calc cost
to_goal_cost = config.to_goal_cost_gain * calc_to_goal_cost(trajectory, goal)
speed_cost = config.speed_cost_gain * (config.max_speed - trajectory[-1, 3])
ob_cost = config.obstacle_cost_gain * calc_obstacle_cost(trajectory, ob, config)
final_cost = to_goal_cost + speed_cost + ob_cost
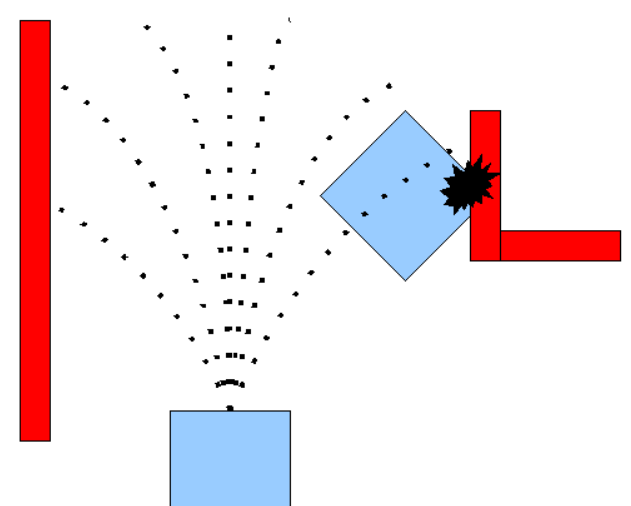
運作示意
在原基礎上,把其他速度視窗内的軌迹也畫出來了,但是因為選cost最小的也就是紅色那個哈
這麼一看我好像知道我曾經用ROS DWA那邊有啥問題了 重新整理路徑dt太快了?走一下發現下一步的軌迹需要左移,然後右移,然後左移 emmm 這樣就S形了?或者是把障礙物的cost因子調低一點?好像是看到了就躲一下,進了再躲一下;然後再貼一下ROS那邊的(我找到了我大學畢設答辯的PPT截圖出來的 hhh)其實當時我答辯錄屏了,但是當時錄制的時候忘記點語音了 然後就是無聲的,hhh 留個留念的機會都沒有了
總結
這麼一看 比frenet簡單太多了 hhhh 畢竟是1997年的了,frenet都是2010年的了:Frenet 部落格園的論文閱讀與代碼執行個體
主要在于:
- DWA這篇的空間一直以笛卡爾坐标系,也不沒有sd坐标系 說有什麼固定的線,也正是因為如此DWA通常作為小型室内無明确道路的機器人首選的局部規劃器
- frenet那篇以考慮加加速度 jerk來作為cost,考慮了車輛乘坐時的舒适度就是加速度的加速度
- Frenet考慮了沿着某個道路的采樣方式,也就是說有某個固定道路線去做行駛,遇到障礙物了再避障,這也符合我們實際駕駛道路車的行為
- Frenet考慮障礙物的東西更多,縱向運動時的跟車,彙入等等 是以常常作為道路無人車局部采樣規劃的首選
至此,再次“複習”完一個,這麼看當初問阿冰哥的答案也能更懂了: