線性回歸——最小二乘法（二）

上篇文章中介紹了單變量線性回歸，為什麼說時單變量呢，因為它隻有單個特征，其實在很多場景中隻有單各特征時遠遠不夠的，當存在多個特征時，我們再使用之前的方法來求特征系數時是非常麻煩的，需要一個特征系數一個偏導式，而卻最要命的時特性的增長時及其迅猛的，幾十、幾百、幾千……

單變量線性回歸：

多變量線性回歸：

　　是以從這裡我們開始将介紹線性回歸的另一種更友善求解多變量線性回歸的方式：最小二乘法矩陣形式；

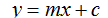
模型變換

　　線性回歸的标量形式：

　　這裡把上訴式子中的系數m與誤差c轉換為向量（為了統一從下面開始使用

表示c與m）,把式子中c看成是1c，把1與特征x也轉換為向量；

是以有：

損失函數

　　損失函數也可以變為：

　　根據矩陣乘積轉置規則損失函數可以進一步化簡為：

偏導數

　　還是和之前一樣求損失函數L的極小值，是以求上式L關于W的偏導數；

向量微分常用等式

求L關于W的偏導數：

因為

則有：

W則是通過矩陣形式求出來的最小乘法的解；

示例

　　下面還是先使用上次的那組資料進行線性拟合，然後再使用多變量資料再次進行線性拟合已驗證上訴算法：

單變量線性回歸示例：

這裡使用上面得到的最小二乘法矩陣形式公式對以下資料集進行線性拟合：

n	x	y
1	2	4
	6	8
3	9	12
	13	21

x、y的矩陣為：

根據公式求w

以下子求整個式子不好求，我們可以先分解該公式；

是以，也就是c=-0.23092,m=1.53092

線性回歸函數可以寫成：y = 1.53092x -0.23092

預測y的值：

y = 1.53092 * 2 - 0.23092=2.83092

y = 1.53092 * 6 - 0.23092=8.9546

y = 1.53092 * 9 - 0.23092=13.54736

y = 1.53092 * 13- 0.23092=19.67104

　　與上偏文章直接求關于m與c的偏導得出來的結果幾乎一樣（因為小數點不同是以精度有所差異）；下篇文章我們将使用本篇文章裡的最小二乘法矩陣形式處理多變量的情況；

參考資料：

https://zh.wikipedia.org/zh/最小二乘法

a first course in machine learning

文章首發位址：Solinx

http://www.solinx.co/archives/721