并查集顧名思義就是有“合并集合”和“查找集合中的元素”兩種操作的關于資料結構的一種算法。
算法
用集合中的某個元素來代表這個集合,該元素稱為集合的代表元。
一個集合内的所有元素組織成以代表元為根的樹形結構。
對于每一個元素 parent[x]指向x在樹形結構上的父親節點。如果x是根節點,則令parent[x] = x。
對于查找操作,假設需要确定x所在的的集合,也就是确定集合的代表元。可以沿着parent[x]不斷在樹形結構中向上移動,直到到達根節點。
判斷兩個元素是否屬于同一集合,隻需要看他們的代表元是否相同即可。
路徑壓縮
為了加快查找速度,查找時将x到根節點路徑上的所有點的parent設為根節點,該優化方法稱為壓縮路徑。
使用該優化後,平均複雜度可視為Ackerman函數的反函數,實際應用中可粗略認為其是一個常數。
用途
1、維護無向圖的連通性。支援判斷兩個點是否在同一連通塊内。
2、判斷增加一條邊是否會産生環:用在求解最小生成樹的Kruskal算法裡。
代碼實作
LeetCode 547 朋友圈
班上有 N 名學生。其中有些人是朋友,有些則不是。他們的友誼具有是傳遞性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那麼我們可以認為 A 也是 C 的朋友。所謂的朋友圈,是指所有朋友的集合。
給定一個 N * N 的矩陣 M,表示班級中學生之間的朋友關系。如果Mi = 1,表示已知第 i 個和 j 個學生互為朋友關系,否則為不知道。你必須輸出所有學生中的已知的朋友圈總數。
使用并查集實作:
public class Union {
class UF {
// 連通分量個數
private int count;
// 存儲一棵樹
private int[] parent;
// 記錄樹的“重量”
private int[] size;
public UF(int n) {
this.count = n;
parent = new int[n];
size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 小樹接到大樹下面,較平衡
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
private int find(int x) {
while (parent[x] != x) {
// 進行路徑壓縮
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
public int count() {
return count;
}
}
public int findCircleNum(int[][] M) {
int n = M.length;
UF uf = new UF(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
if (M[i][j] == 1)
uf.union(i, j);
}
}
return uf.count();
}
} 關于并查集的圖文解說
為了解釋并查集的原理,下面的内容來自網友部落格。
話說江湖上散落着各式各樣的大俠,有上千個之多。他們沒有什麼正當職業,整天背着劍在外面走來走去,碰到和自己不是一路人的,就免不了要打一架。但大俠們有一個優點就是講義氣,絕對不打自己的朋友。而且他們信奉“朋友的朋友就是我的朋友”,隻要是能通過朋友關系串聯起來的,不管拐了多少個彎,都認為是自己人。這樣一來,江湖上就形成了一個一個的群落,通過兩兩之間的朋友關系串聯起來。而不在同一個群落的人,無論如何都無法通過朋友關系連起來,于是就可以放心往死了打。但是兩個原本互不相識的人,如何判斷是否屬于一個朋友圈呢?
我們可以在每個朋友圈内推舉出一個比較有名望的人,作為該圈子的代表人物,這樣,每個圈子就可以這樣命名“齊達内朋友之隊”“羅納爾多朋友之隊”……兩人隻要互相對一下自己的隊長是不是同一個人,就可以确定敵友關系了。
但是還有問題啊,大俠們隻知道自己直接的朋友是誰,很多人壓根就不認識隊長,要判斷自己的隊長是誰,隻能漫無目的的通過朋友的朋友關系問下去:“你是不是隊長?你是不是隊長?”這樣一來,隊長面子上挂不住了,而且效率太低,還有可能陷入無限循環中。于是隊長下令,重新組隊。隊内所有人實行分等級制度,形成樹狀結構,我隊長就是根節點,下面分别是二級隊員、三級隊員。每個人隻要記住自己的上級是誰就行了。遇到判斷敵友的時候,隻要一層層向上問,直到最高層,就可以在短時間内确定隊長是誰了。由于我們關心的隻是兩個人之間是否連通,至于他們是如何連通的,以及每個圈子内部的結構是怎樣的,甚至隊長是誰,并不重要。是以我們可以放任隊長随意重新組隊,隻要不搞錯敵友關系就好了。于是,門派産生了。
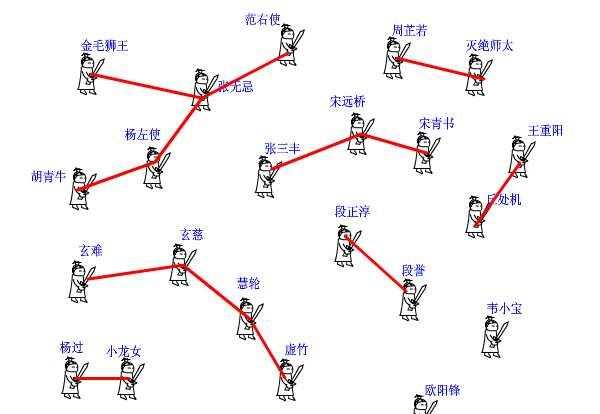
下面我們來看并查集的實作。 int pre[1000]; 這個數組,記錄了每個大俠的上級是誰。大俠們從1或者0開始編号(依據題意而定),pre[15]=3就表示15号大俠的上級是3号大俠。如果一個人的上級就是他自己,那說明他就是掌門人了,查找到此為止。也有孤家寡人自成一派的,比如歐陽鋒,那麼他的上級就是他自己。每個人都隻認自己的上級。比如胡青牛同學隻知道自己的上級是楊左使。張無忌是誰?不認識!要想知道自己的掌門是誰,隻能一級級查上去。 find這個函數就是找掌門用的,意義再清楚不過了(路徑壓縮算法先不論,後面再說)。
int find(int x) //查找我(x)的掌門
{
int r=x; //委托 r 去找掌門
while (pre[r ]!=r) //如果r的上級不是r自己(也就是說找到的大俠他不是掌門 = =)
r=pre[r ] ; // r 就接着找他的上級,直到找到掌門為止。
return r ; //掌門駕到~~~
} 再來看看join函數,就是在兩個點之間連一條線,這樣一來,原先它們所在的兩個闆塊的所有點就都可以互通了。這在圖上很好辦,畫條線就行了。但我們現在是用并查集來描述武林中的狀況的,一共隻有一個pre[]數組,該如何實作呢? 還是舉江湖的例子,假設現在武林中的形勢如圖所示。虛竹小和尚與周芷若MM是我非常喜歡的兩個人物,他們的終極boss分别是玄慈方丈和滅絕師太,那明顯就是兩個陣營了。我不希望他們互相打架,就對他倆說:“你們兩位拉拉勾,做好朋友吧。”他們看在我的面子上,同意了。這一同意可非同小可,整個少林和峨眉派的人就不能打架了。這麼重大的變化,可如何實作呀,要改動多少地方?其實非常簡單,我對玄慈方丈說:“大師,麻煩你把你的上級改為滅絕師太吧。這樣一來,兩派原先的所有人員的終極boss都是師太,那還打個球啊!反正我們關心的隻是連通性,門派内部的結構不要緊的。”玄慈一聽肯定火大了:“我靠,憑什麼是我變成她手下呀,怎麼不反過來?我抗議!”抗議無效,上天安排的,最大。反正誰加入誰效果是一樣的,我就随手指定了一個。這段函數的意思很明白了吧?
void join(int x,int y) //我想讓虛竹和周芷若做朋友
{
int fx=find(x),fy=find(y); //虛竹的老大是玄慈,芷若MM的老大是滅絕
if(fx!=fy) //玄慈和滅絕顯然不是同一個人
pre[fx ]=fy; //方丈隻好委委屈屈地當了師太的手下啦
} 路徑壓縮,就是調整掌門結構,都變成2級關系
再來看看路徑壓縮算法。建立門派的過程是用join函數兩個人兩個人地連接配接起來的,誰當誰的手下完全随機。最後的樹狀結構會變成什麼胎唇樣,我也完全無法預計,一字長蛇陣也有可能。這樣查找的效率就會比較低下。最理想的情況就是所有人的直接上級都是掌門,一共就兩級結構,隻要找一次就找到掌門了。哪怕不能完全做到,也最好盡量接近。這樣就産生了路徑壓縮算法。 設想這樣一個場景:兩個互不相識的大俠碰面了,想知道能不能揍。 于是趕緊打電話問自己的上級:“你是不是掌門?” 上級說:“我不是呀,我的上級是誰誰誰,你問問他看看。” 一路問下去,原來兩人的最終boss都是東廠曹公公。 “哎呀呀,原來是記己人,西禮西禮,在下三營六組白面葫蘆娃!” “幸會幸會,在下九營十八組仙子狗尾巴花!” 兩人高高興興地手拉手喝酒去了。 “等等等等,兩位同學請留步,還有事情沒完成呢!”我叫住他倆。 “哦,對了,還要做路徑壓縮。”兩人醒悟。 白面葫蘆娃打電話給他的上級六組長:“組長啊,我查過了,其習偶們的掌門是曹公公。不如偶們一起及接拜在曹公公手下吧,省得級别太低,以後查找掌門麻環。” “唔,有道理。” 白面葫蘆娃接着打電話給剛才拜訪過的三營長……仙子狗尾巴花也做了同樣的事情。 這樣,查詢中所有涉及到的人物都聚集在曹公公的直接上司下。每次查詢都做了優化處理,是以整個門派樹的層數都會維持在比較低的水準上。路徑壓縮的代碼,看得懂很好,看不懂也沒關系,直接抄上用就行了。總之它所實作的功能就是這麼個意思。