本篇文章将從貝葉斯公式出發,探究貝葉斯到底是啥,以及其在認知層面的巨大作用。不過據說每出現 1 個公式,文章閱讀将下降 1/3。
華為大佬說:人工智能就是統計學。在我眼中,貝葉斯公式就是統計學走向機器學習的起點。
貝葉斯公式
貝葉斯定理(Bayes’s Rule):如果有k個互相獨立事件 A1,A2···,Ak并且,P (A1) + P(A2) + ... + p(Ak)= 1 和一個可以觀測到的事件 B,那麼有:
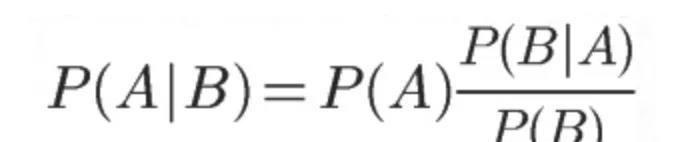
這個就是貝葉斯公式,相當簡潔。
公式中有幾個關鍵概念:
P(A)為先驗機率,即在觀察事件B之前得到的事件A的假設機率
P(A|B) 為後驗機率,即在觀察事件B後得到新資料後計算該假設A的機率
P(B|A)為似然度,即在該假設A下得到這一觀察資料 B 的機率
P(B)為标準化常量,即在任何假設下得到這一觀察資料 B 的機率
用一句人話表達則是:
後驗機率 = 先驗機率×似然度
說到貝葉斯,必然離不開條件機率。
01 / 條件機率
條件機率的公式
條件機率翻譯過來就是事件B發生條件下A發生的機率,等于 AB 同時發生的機率比上 B 發生的機率。看着和貝葉斯及其相似, 實際上貝葉斯公式也是通過條件機率來證明的,具體就不贅述了。
02 / 貝葉斯公式 VS 條件機率
條件機率是頻率統計思維,通過已知的資訊去計算事件出現機率,我們稱之為正向機率;貝葉斯公式反其道而行之,通過實驗結果去反推出現實驗結果的原因,我們稱之為逆機率
上面這段話聽着太拗口。我們用經典的摸球行為進行說明。
1.選擇略微複雜點的場景:有兩個桶,A 桶中有白球 7 個,黑球 3 個;B 桶中有白球 3 個,黑球 7 個。随機選擇一個桶,有放回的抓球。
2.條件機率解決的問題是:摸到白球的機率是多少?
3.貝葉斯公式解決的問題是:我們摸 5 次,出現 3 次白球,2 次黑球,從 A 桶摸球的機率。
條件機率解法:
通過先驗知識,我們可以知道随機選擇一個桶機率 P(A)=P(B)=0.5
通過頻率統計知識,我們可以算出條件機率 P(白球|A)=0.7 P(白球|B)=0.3
是以在已知知識的情況下,我們預測摸到白球的機率 0.5X0.7 + 0.3X0.7 = 0.5
貝葉斯公式解法:
那貝葉斯需要計算的是 P(A|x 球),出現x顔色球條件下選擇A桶的機率。我們從第一次摸白球開始計算。
P(A|白球 1) = P(A) x P(白球|A)/P(白球) = 0.5 x 0.7/0.5 = 0.7
這個結果的含義是第一次出現白球,則我們随機選擇 A 桶的機率将從 0.5 變為 0.7
同樣的計算第二次選擇白球的機率 P(A|白球 2) = P(A) x P(白球|A)/P(白球) = 0.7 x 0.7/(0.7x0.7 + 0.3x0.3) = 0.8448
重複計算下來,可以得到 A 桶的機率是 0.7
即可以了解為每次不同的觀察結果,對于原因會産生影響。白球增加 A 桶的機率,黑球減少 A 桶的機率。
可以看到貝葉斯更加符合我們認知世界的方式。現實世界中,我們往往能觀察到大量的現象,我們更加關心現象背後的原因。比如一段文本出現大量的特征,我們會去判斷是不是垃圾郵件;比如一個女生同意和你吃飯,是不是對你有好感。
貝葉斯與認知
上面的例子偏向于太學術。按照人話來看貝葉斯公式其實就是後驗機率 = 先驗機率×似然度。
簡單的,我們認知一個新的事物前,先驗機率就是我們的感性認知。似然度則是我們需要深度思考,去認真對待的調節因子。
可以看到:
似然度 > 1, 加強先驗機率/感性認知
似然度 = 1,後驗機率=先驗機率
似然度 < 1, 減弱先驗機率/感性認知
從上面的例子可以看到,似然度的影響因子主要有兩個:一是增加新資料的量,二是增加新資料的質。
依然舉個栗子:
男同學追女同學,總會好奇女孩子是否對自己有興趣。
自戀的同學會說,我的女神一直看我,肯定對我有好感。
理性的同學将這個場景轉化為貝葉斯公式:P(好感|看我)= 先驗感覺 * 似然度。
從理性角度,先驗經驗“看我和對我有好感”其實沒有太多必然聯系,是以機率上可以按 0.5。我們為了求證 P(好感|看我)确實很高,我們就需要更多的觀察資料來支援我們的結論。
比如女生是高冷女孩,那麼她認真看你,這個新增的資料代表每次看你的品質是很高的,當然似然度會大于 1.
如果女生也經常盯着男生看,但是看我的次數更多,這個其實是增加了資料的量,似然度也會大于 1。
是以理性的人判斷 P(好感|看我) 會比較高。
可以看到自戀的同學是将先驗經驗設定得太高,以至于忽略了似然度的觀察,理性的同學弱化先驗經驗,加強了似然函數。這其實對應了兩類人,強經驗弱似然函數和弱經驗強似然函數。如下圖
兩種人不能說誰優于誰,強經驗的人,後驗機率的波動較小。弱經驗的人,根據貝葉斯公式,更利于輸入新的資料,完成後驗機率的更新。
總結
2020 年,提升認知成為共識。按照貝葉斯定理,處于認知更新的我們,應該弱化我們的經驗,觀察世界強化似然度,進而更新自己的觀點。像喬幫主所說:stay hungry。
在幾百年前,貝葉斯就給出了從逆機率思考的科學架構,實在是佩服。