雲栖号資訊:【 點選檢視更多行業資訊】
在這裡您可以找到不同行業的第一手的上雲資訊,還在等什麼,快來!
之前介紹了一種最簡單構造決策樹的方法——ID3算法,也就是每次選擇一個特征進行拆分資料。這個特征有多少個取值那麼就劃分出多少個分叉,整個建樹的過程非常簡單。
如果你還不會決策樹,那你一定要進來看看
既然我們已經有了ID3算法可以實作決策樹,那麼為什麼還需要新的算法?顯然一定是做出了一些優化或者是進行了一些改進,不然新算法顯然是沒有意義的。是以在我們學習新的算法之前,需要先搞明白,究竟做出了什麼改進,為什麼要做出這些改進。
一般來說,改進都是基于缺點和不足的,是以我們先來看看ID3算法的一些問題。
其中最大的問題很明顯,就是它無法處理連續性的特征。不能處理的原因也很簡單,因為ID3在每次在切分資料的時候,選擇的不是一個特征的取值,而是一個具體的特征。這個特征下有多少種取值就會産生多少個分叉,如果使用連續性特征的話,比如說我們把西瓜的直徑作為特征的話。那麼理論上來說每個西瓜的直徑都是不同的,這樣的資料丢進ID3算法當中就會産生和樣本數量相同的分叉,這顯然是沒有意義的。
其實還有一個問題,藏得會比較深一點,是關于資訊增益的。我們用劃分前後的資訊熵的差作為資訊增益,然後我們選擇帶來最大資訊增益的劃分。這裡就有一個問題了,這會導緻模型在選擇的時候,傾向于選擇分叉比較多的特征。極端情況下,就比如說是連續性特征好了,每個特征下都隻有一個樣本,那麼這樣算出來得到的資訊熵就是0,這樣得到的資訊增益也就非常大。這是不合理的,因為分叉多的特征并不一定劃分效果就好,整體來看并不一定是有利的。
針對這兩個問題,提出了改進方案,也就是說C4.5算法。嚴格說起來它并不是獨立的算法,隻是ID3算法的改進版本。
下面我們依次來看看C4.5算法究竟怎麼解決這兩個問題。
資訊增益比
首先,我們來看資訊增益的問題。前面說了,如果我們單純地用資訊增益去篩選劃分的特征,那麼很容易陷入陷阱當中,選擇了取值更多的特征。
針對這個問題,我們可以做一點調整,我們把資訊增益改成資訊增益比。所謂的資訊增益比就是用資訊增益除以我們這個劃分本身的資訊熵,進而得到一個比值。對于分叉很多的特征,它的自身的資訊熵也會很大。因為分叉多,必然導緻純度很低。是以我們這樣可以均衡一下特征分叉帶來的偏差,進而讓模型做出比較正确的選擇。
我們來看下公式,真的非常簡單:
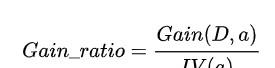
這裡的D就是我們的訓練樣本集,a是我們選擇的特征,IV(a)就是這個特征分布的資訊熵。
我們再來看下IV的公式:
解釋一下這裡的值,這裡的V是特征a所有取值的集合。自然就是每一個v對應的占比,是以這就是一個特征a的資訊熵公式。
處理連續值
C4.5算法對于連續值同樣進行了優化,支援了連續值,支援的方式也非常簡單,對于特征a的取值集合V來說,我們選擇一個門檻值t進行劃分,将它劃分成小于t的和大于t的兩個部分。
也就是說C4.5算法對于連續值的切分和離散值是不同的,對于離散值變量,我們是對每一種取值進行切分,而對于連續值我們隻切成兩份。其實這個設計非常合理,因為對于大多數情況而言,每一條資料的連續值特征往往都是不同的。而且我們也沒有辦法很好地确定對于連續值特征究竟分成幾個部分比較合理,是以比較直覺的就是固定切分成兩份,總比無法用上好。
在極端情況下,連續值特征的取值數量等于樣本條數,那麼我們怎麼選擇這個門檻值呢?即使我們周遊所有的切分情況,也有n-1種,這顯然是非常龐大的,尤其在樣本數量很大的情況下。
針對這個問題,也有解決的方法,就是按照特征值排序,選擇真正意義上的切分點。什麼意思呢,我們來看一份資料:
這份資料是我們隊西瓜直徑這個特征排序之後的結果,我們可以看出來,訓練目标改變的值其實隻有3個,分别是直徑5,7還有8的時候,我們隻需要考慮這三種情況就好了,其他的情況可以不用考慮。
我們綜合考慮這兩點,然後把它們加在之前ID3模型的實作上就好了。
代碼實作
光說不練假把式,我們既然搞明白了它的原理,就得自己親自動手實作以下才算是真的了解,很多地方的坑也才算是真的懂。我們基本上可以沿用之前的代碼,不過需要在之前的基礎上做一些修改。
首先我們先來改造構造資料的部分,我們依然沿用上次的資料,學生的三門考試等級以及它是否通過達标的資料。我們認為三門成績在150分以上算是達标,大于70分的課程是2等級,40-70分之間是1等級,40分以下是0等級。在此基礎上我們增加了分數作為特征,我們在分數上增加了一個誤差,避免模型直接得到結果。
由于我們需要計算資訊增益比,是以需要開發一個專門的函數用來計算資訊增益比。由于這一次的資料涉及到了連續型特征,是以我們需要多傳遞一個門檻值,來判斷是否是連續性特征。如果是離散型特征,那麼門檻值為None,否則為具體的值。
split_dataset函數也需要修改,因為我們拆分的情況多了一種根據門檻值拆分,通過判斷門檻值是否為None來判斷進行門檻值劃分還是特征劃分。
前面說了我們在選擇門檻值的時候其實并不一定要周遊所有的取值,因為有些取值并不會引起label分布的變化,對于這種取值我們就可以忽略。是以我們需要一個函數來擷取門檻值所有的可能性,這個也很簡單,我們直接根據門檻值排序,然後周遊觀察label是否會變化,記錄下所有label變化位置的值即可:
有了這些方法之後,我們需要開發選擇拆分值的函數,也就是計算所有特征的資訊增益比,找到資訊增益比最大的特征進行拆分。其實我們将前面拆分和擷取所有門檻值的函數都開發完了之後,要尋找最佳的拆分點就很容易了,基本上就是利用一下之前開發好的代碼,然後搜尋一下所有的可能性:
到這裡,基本方法就開發完了,隻剩下建樹和預測兩個方法了。這兩個方法和之前的代碼改動都不大,基本上就是細微的變化。我們先來看建樹,建樹唯一的不同點就是在dict當中需要額外存儲一份門檻值的資訊。如果是None表示離散特征,不為None為連續性特征,其他的邏輯基本不變。
最後是預測的函數,邏輯和之前一樣,隻不過加上了門檻值是否為None的判斷而已,應該非常簡單:
總結
到這裡整個決策樹的C4.5算法就開發完了,整體來說由于加上了資訊增益比以及連續性特征的邏輯,是以整體的代碼比之前要複雜一些,但是基本上的邏輯和套路都是一脈相承的,基本上沒什麼太大的變化。
決策樹說起原理來非常簡單,但是很多細節如果沒有親自做過是意識不到的。比如說連續性特征的門檻值集合應該怎麼找,比如說連續性特征和離散型的特征混合的情況,怎麼在代碼當中區分,等等。隻有實際動手做過,才能意識到這些問題。雖然平時也用不到決策樹這個模型,但是它是很多進階模型的基礎,吃透它對後面的學習和進階非常有幫助,如果有空,推薦大家都親自試一試。
【雲栖号線上課堂】每天都有産品技術專家分享!
課程位址:
https://yqh.aliyun.com/live立即加入社群,與專家面對面,及時了解課程最新動态!
【雲栖号線上課堂 社群】
https://c.tb.cn/F3.Z8gvnK
原文釋出時間:2020-05-29
本文作者:承志
本文來自:“
掘金”,了解相關資訊可以關注“掘金”