二叉搜尋樹(Binary Search Tree)為非線性結構,樹與連結清單一樣為動态資料結構也可稱二叉搜尋樹為多個連結清單所組成實作的,由于二叉搜尋樹性能比較高是以屬于比較常用的資料結構;二叉搜尋樹每個節點除了Key外還存在指向左子樹的Left節點與指向右子樹的Right節點,如左或右子樹不存在則該節點值為Null;
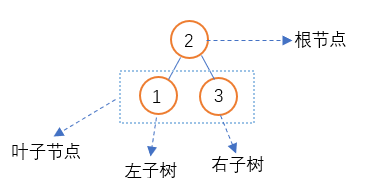
二叉搜尋樹為一種特殊的二叉樹,與二叉樹有類似的結構,存在唯一的根節點,每一個節點最多隻存在兩個子節點分别為左子樹與右子樹,當某個節點不存在任何子節點時又稱為葉子節點,每個節點有且隻有一個父節點,二叉樹具有與生俱來的遞歸結構;
1、 唯一根節點
2、 每個節點最多隻有兩個節點
3、 葉子節點不存在任何子節點
4、 隻有唯一父節點
二叉搜尋樹與普通二叉樹的根本差別在于二叉搜尋樹中任意一個節點的值大于該節點左子樹中任意節點的值,小于該節點右子樹中任意一個節點的值;
1、 節點的左子樹任意一個節點值比目前節點值小
2、 節點的右子樹任意一個節點值比目前節點值大
二叉搜尋樹的實作
1、二叉搜尋樹定義
根據二叉搜尋樹的特性先定義該資料類型的結構;
type BST struct {
root *TreeNode
size int
compare Comparable
}
type TreeNode struct {
e interface{}
left *TreeNode
right *TreeNode
}
BST:為定義的二叉搜尋樹自定義對象
TreeNode:為樹中每個節點的節點自定義對象
compare:為定義的用于樹中節點元素進行資料對比的對象
size:二叉搜尋樹的元素個數
root:樹的根節點
e:節點元素值
left:左子樹
right:右子樹
2、具體二叉搜尋樹方法實作
/**
元素比較
*/
type Comparable func(c1 interface{}, c2 interface{}) int
/**
建立二叉樹
*/
func NewBST(comparable Comparable) *BST {
return &BST{size: 0, root: nil, compare: comparable}
}
/**
建立節點
*/
func newTreeNode(e interface{}) *TreeNode {
return &TreeNode{e: e, left: nil, right: nil}
}
/**
二叉樹大小
*/
func (t *BST) Size() int {
return t.size
}
/**
是否未空
*/
func (t *BST) IsEmpty() bool {
return t.size == 0
}
/**
添加元素
*/
func (t *BST) Add(e interface{}) {
t.root = t.add(t.root, e)
}
/**
用于遞歸添加元素
*/
func (t *BST) add(node *TreeNode, e interface{}) *TreeNode {
if node == nil {
t.size++
return newTreeNode(e)
}
if t.compare(e, node.e) < 0 {
node.left = t.add(node.left, e)
} else if t.compare(e, node.e) > 0 {
node.right = t.add(node.right, e)
}
return node
}
/**
删除元素
*/
func (t *BST) Remove(e interface{}) {
t.root = t.remove(t.root, e)
}
/**
查找最小節點
*/
func (t *BST) Minimum() *TreeNode {
return t.minimum(t.root)
}
func (t *BST) minimum(node *TreeNode) *TreeNode {
if node.left == nil {
return node
}
return t.minimum(node.left)
}
func (t *BST) remove(node *TreeNode, e interface{}) *TreeNode {
if node == nil {
return nil
}
//值與目前節點值比較
if t.compare(e, node.e) < 0 {
node.left = t.remove(node.left, e)
return node
} else if t.compare(e, node.e) > 0 {
node.right = t.remove(node.right, e)
return node
} else { // t.compare(e,node.e)==0{
//需要删除的節點為目前節點時
if node.left == nil {
//右子樹頂上
var rightNode = node.right
node.right = nil
t.size--
return rightNode
} else if node.right == nil {
//左子樹頂上
var leftNode = node.left
node.left = nil
t.size--
return leftNode
}
//左右節點均不為空,找到比目前節點大的最小節點(此節點為右子樹最小節點)
//用右子樹最小節點替代需要删除的目前節點
var successor = t.minimum(node.right)
successor.right = t.removeMin(node.right)
successor.left = node.left
node.left = nil
node.right = nil
return successor
}
}
簡要介紹
由于二叉搜尋樹所具有的特性,所有很多操作都可用遞歸來實作,比如元素的添加、删除、查找等等;
1、元素添加
二叉搜尋樹的元素添加關鍵在于遞歸與元素值的比較,關鍵三點:1、節點為空建立新節點為目前節點;2、元素比目前節點小,在左子樹添加;元素比目前節點大,在右子樹添加;
2、元素删除
二叉搜尋樹的元素删除關鍵在于删除節點後調整樹結構已保持樹具備左子樹小于根節點值,右子樹大于跟節點值的特性;
元素删除關鍵點:
1、 小于目前節點在左子樹查找删除
2、 大于目前節點在右子樹查找删除
3、 需删除的節點左子樹不存在,右子樹頂上
4、 需删除的節點右子樹不存在,左子樹頂上
5、 需删除節點左右子樹均存在,找到比該節點大的最小節點(右子樹最小節點),用該節點替換需要删除的節點
由于二叉搜尋樹的特性,通過中序周遊可得到排序好的資料,二叉搜尋樹的搜尋、插入、删除時間複雜度為O(log(n)),n為樹的深度;
參考資料: 《算法四》