相信大家對排序算法都非常熟悉了,快速排序、堆排序、歸并排序等等。如果我們想在一個很大的資料集上進行排序,能利用上多核,甚至是分布式叢集,有什麼辦法麼?
本文就介紹一種并行排序算法:并行正則采樣排序算法(Parallel Sorting by Regular Sampling),簡稱 PSRS 算法。
PSRS 算法過程
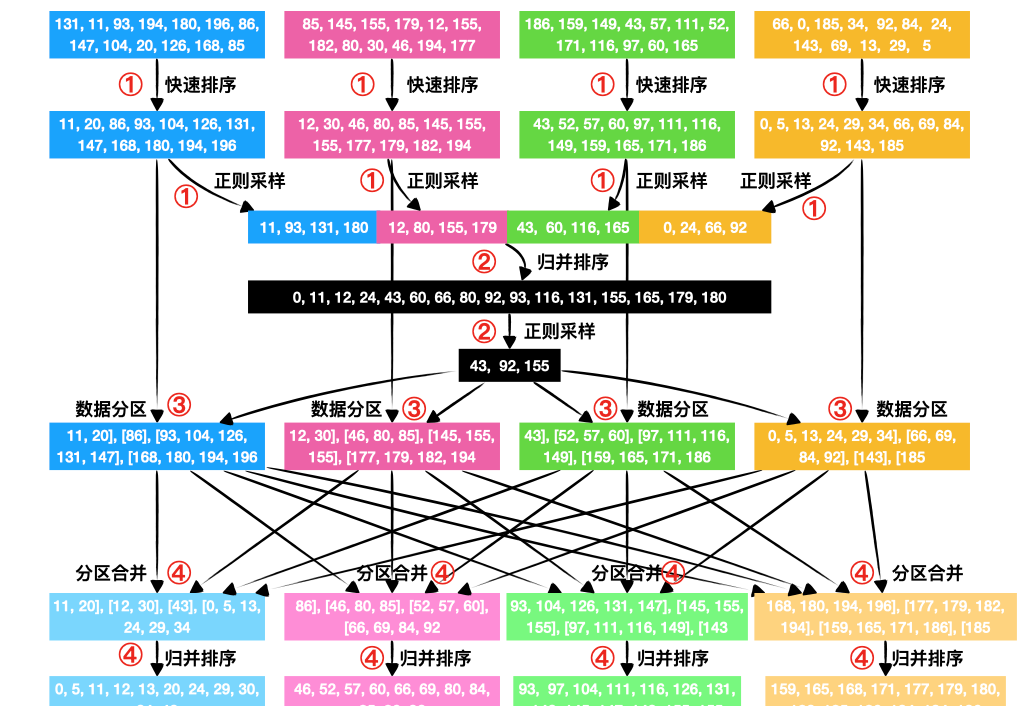
PSRS 算法的整個過程分為四步,如圖所示,我們拆解開來講。
現在假設我們有一個數組,有 48 個元素,現在資料被分成4份,即有4個分區。
階段1,每個分區分别排序,并正則采樣
我們對每個分區的資料調用快速排序,這樣每個分區都是排好的資料。接着,我們從排好序的資料裡正則采樣4個資料。所謂正則,即有規律的,這裡我們就每隔4個元素采樣一個元素。
階段2,歸并采樣資料,選出關鍵點
前面四個分區産生了4份采樣資料,收集之,然後調用歸并排序讓他們有序。接着,我們從中選出 p - 1 (p 是分區個數)個關鍵點,這裡還是正則采樣的方式。
階段3,資料分區
此時将關鍵點資料廣播給每個分區,每個分區就可以根據關鍵點,将資料分成4份,使得每個資料落在各自的範圍内。
階段4,合并資料,歸并排序
最後一個階段是一個 shuffle 階段,即每個下遊都依賴前面的所有上遊。此時每個分區将上遊分好的資料收集起來,最終再進行一個歸并排序。這樣,我們最終的結果就是整體排序的了。
整個過程中,階段1、階段3 和 階段4 可以并行。
MPI 的實作可以參考
這裡。
PSRS 算法在 Mars 中的應用
Mars以并行和分布式化 Python 資料科學棧為目标,PSRS 算法能很好解決并行排序問題,是以,Mars 中和排序有關的操作都是基于 PSRS 算法實作的。
以張量排序為例。
首先我們通過 Numpy 建立 1 億個元素的數組。
In [1]: import numpy as np
In [2]: a = np.random.rand(1_0000_0000)
In [3]: a.nbytes
Out[3]: 800000000 我們來看看使用 Numpy 的排序需要多久。
In [4]: %time np.sort(a)
CPU times: user 10.8 s, sys: 394 ms, total: 11.2 s
Wall time: 9.4 s
Out[4]:
array([1.05764619e-10, 5.86309734e-09, 1.76225879e-08, ...,
9.99999976e-01, 9.99999983e-01, 9.99999998e-01]) 接着,我們來看看基于 PSRS 算法的 Mars tensor 排序需要多長時間。
In [10]: t = mt.tensor(a, chunk_size=1500_0000)
In [12]: %time mt.sort(t).execute()
CPU times: user 18.7 s, sys: 7.03 s, total: 25.7 s
Wall time: 2.66 s 在我的筆記本上,可以看到 Numpy 的排序時長是 Mars 的 3.53 倍。
總結
本文介紹了并行正則排序算法,這個算法也在 Mars 項目裡得到了廣泛的使用。
如果對 Mars 感興趣,可以關注
Mars 團隊專欄,或者釘釘掃二維碼加入 Mars 讨論群。