持續到現在的新冠疫情,已經改變了千萬人的命運,其中也包括我
面對這麼殘暴的天災,我做了一個預測模型,希望能貢獻自己一點微薄的力量,讓天災早點過去
有首歌唱得好:
讓我悲也好,讓我悔也好,讓疫情過去沒煩惱;讓我苦也好,讓我累也好,讓我看見大家的笑……
好了,廢話結束,進入正題:
在這之前,github上已經有一個預測項目了:
https://github.com/YiranJing/Coronavirus-Epidemic-2019-nCov于是我将他的源碼down下來仔細看了看
該項目作者實作了自己的SIR和SEIR模型
(兩種經典的傳染病模型:
https://baike.baidu.com/item/%E4%BC%A0%E6%9F%93%E7%97%85%E6%A8%A1%E5%9E%8B/5130035?fr=aladdin)
而模型的關鍵部分是定義了一個分布函數:
def Binomial_log_like(n: int, p: float, k: int):
loglik = lgamma(n+k+1) - lgamma(k+1) - lgamma(n+1) + k*np.log(p) + n*np.log(1-p) 上述公式定義了對疫情傳染人數趨勢的一個假設公式
顧名思義,他将疫情的傳染人數曲線看作二進制對數分布
使用SIR和SEIR構模組化型是否恰當呢?
這兩種傳染病動力學模型,其實都未考慮隔離措施的因素
都是建立在自然傳播和自然康複的基礎上,是以如果要做更客觀的預測,需要考慮人類隔離活動的影響
而疫情資料實際的分布是否滿足這種分布呢?我們取出曆史資料看看:
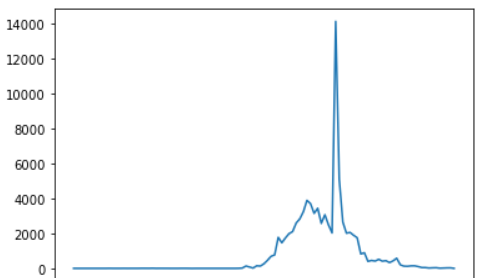
國内每天新增病例趨勢
從上圖可以發現,新增病例曲線總體上更有點類似于伽馬分布
而曲線中殘缺的部分,猜測則是由于政府相關部門采取了強有力的隔離措施,導緻了病毒傳播的中斷
是以,從宏觀上看,新增病例曲線就是兩種力量不斷對抗的結果:
新增感染數量 = 病毒自然傳播力 - 人類阻斷摩擦力 如果非要用一個實體現象做類比,就好像給往下滾動的雪球踩刹車
假設人類阻斷力在23号封城以後是一個常量(已達到人類能實作的最進階别阻斷)
那麼其實我們就可以用伽馬曲線近似的逼近23号之後的曲線
是以,這裡我自定義了一個控制函數:
def control_curve(x, i0, missing, latency=7, infection_num=2):
"""
傳染曲線,假設過了潛伏期即被隔離
今天傳染人數 = (昨天實際傳染人數 - 昨天隔離人數) * 平均傳染人數
昨天隔離人數 = 七天前實際傳染人數
今天傳染人數 = (昨天實際傳染人數 - 七天前實際傳染人數) * 平均傳染人數
:param x: 傳染時間
:param i0: 初始傳染人數
:param missing: 遺漏率
:param latency: 潛伏期(确切的說,這裡代表平均發病時間,假設發病時間内每天都具有傳染性)
:param infection_num: 平均傳染人數
"""
if x >= latency:
isolated = i0 * (infection_num ** (x - latency))
else:
isolated = 0
day_num = i0 * missing * (infection_num ** x) - isolated
if day_num < 0:
day_num = 0
return day_num 該函數中存在4個未知參數,我們可以利用scipy的優化器自動求解最優值:
from scipy.optimize import curve_fit
def control_curve_list(x, i0, missing, latency, infection_num):
y = list(map(control_curve, x, [i0] * len(x), [missing] * len(x), [latency] * len(x), [infection_num] * len(x)))
return y
popt,pcov = curve_fit(f=control_curve_list, xdata=x_data[:-1], ydata=y_data[:-1]) 通過 curve_fit 曲線拟合函數,我們就可以快速的得到一組近似最優解
拟合出來後,看看效果:
最優參數得到的模型預測120天結果
看起來很光滑呀,實際資料恐怕會比這個粗糙很多
那這個預測值,與實際是否比對呢?
看起來,方差還是比較大的,有沒有辦法得到一個更精确的預測呢?
我們可以大膽假設,人類的隔離力度,在每個階段、每個區域可能都不盡相同
每個時期的參數值可能會略有不同
是以接下來就用貝葉斯優化器對最優參數繼續做更深入的探索:
這裡先引入JS散度,友善貝葉斯優化器對結果進行比較
from bayes_opt import BayesianOptimization
def JS_divergence(p,q):
M=(p+q)/2
return 0.5*scipy.stats.entropy(p, M)+0.5*scipy.stats.entropy(q, M) 再建構一個目标函數,傳回可比較的分值
def result_function(nu, close_contacts, k, I0, E0, T, death_rate):
N = 14 * (10 ** 8)
econ = len(t)
R0 = I0 * (death_rate) * 2
try:
Est = Estimate_parameter(nu=nu, k=close_contacts, t=t, I=I)
eso = Estimate_Wuhan_Outbreak(Est, k=k, N=N, E0=E0, I0=I0, R0=R0, T=T, econ=econ)
result = eso._run_SIER('Forecat', 'China', 'Days after 2019-12-1', death_rate=death_rate, show_Plot=False)
score = JS_divergence(I,result['Infected'])
except Exception as e:
score = 999
print(e)
try:
score = float(score)
except:
score = 999
if score > 999:
score = 999
return -score 然後,根據前面的最優參數,手工設定一些搜尋區間:
rf_bo = BayesianOptimization(
result_function,
{'nu': (1/20, 1/10),
'close_contacts': (5, 15),
'k': (1, 3),
'I0': (1, 10000),
'E0': (0,10000),
'T':(3,14),
'death_rate':(0.2,0.3)
}
) 最後,把我們的優化器跑起來,讓它自己找找
rf_bo.maximize(init_points=5,
n_iter=1000,) 最終,我們就得到了一個相對靠譜的結果:
使用這個參數進行預測,與實際結果的差距就不大了
整套邏輯寫好後,也可以把流程寫成一個pipline,每天自動拟合
這樣,就能不斷的逼近最客觀的結果!
以上就是我分享的思路,有不正确的地方還請大家多多批評!