幹貨：圖解算法——動态規劃系列

動态規劃系列一：爬樓梯

1.1 概念講解

講解動态規劃的資料很多，官方的定義是指把多階段過程轉化為一系列單階段問題，利用各階段之間的關系，逐個求解。概念中的各階段之間的關系，其實指的就是狀态轉移方程。很多人覺得DP難（下文統稱動态規劃為DP），根本原因是因為DP差別于一些固定形式的算法（比如DFS、二分法、KMP），沒有實際的步驟規定第一步第二步來做什麼，是以準确的說，DP其實是一種解決問題的思想。

這種思想的本質是：一個規模比較大的問題（可以用兩三個參數表示的問題），可以通過若幹規模較小的問題的結果來得到的（通常會尋求到一些特殊的計算邏輯，如求最值等）

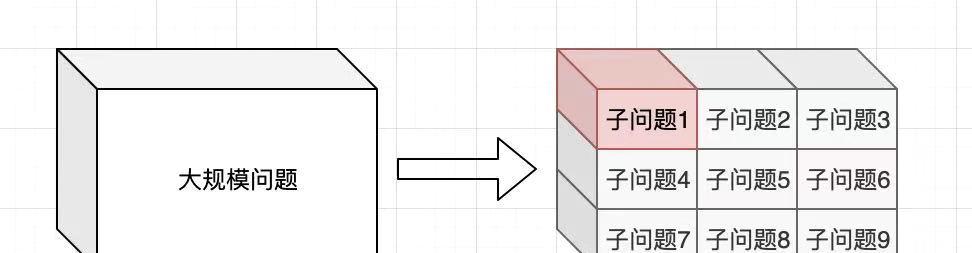
圖1

是以我們一般看到的狀态轉移方程，基本都是這樣：

opt ：指代特殊的計算邏輯，通常為max or min。

i,j,k 都是在定義DP方程中用到的參數。

dp[i] = opt(dp[i-1])+1

dpi = w(i,j,k) + opt(dpi-1)

dpi = opt(dpi-1 + xi, dpi + yj, ...)

每一個狀态轉移方程，多少都有一些細微的差别。這個其實很容易了解，世間的關系多了去了，不可能抽象出完全可以套用的公式。是以我個人其實不建議去死記硬背各種類型的狀态轉移方程。但是DP的題型真的就完全無法掌握，無法歸類進行分析嗎？我認為不是的。在本系列中，我将由簡入深為大家講解動态規劃這個主題。

我們先看上一道最簡單的DP題目，熟悉DP的概念：

題目：假設你正在爬樓梯。需要 n 階你才能到達樓頂。每次你可以爬 1 或 2 個台階。你有多少種不同的方法可以爬到樓頂呢？注意：給定 n 是一個正整數。

示例 1：

輸入：2輸出：2解釋：有兩種方法可以爬到樓頂。

1. 1 階 + 1 階
2. 2 階

示例 2：

輸入：3輸出：3解釋：有三種方法可以爬到樓頂。

1. 1 階 + 1 階 + 1 階
2. 1 階 + 2 階
3. 2 階 + 1 階

1.2 題目圖解

通過分析我們可以明确，該題可以被分解為一些包含最優子結構的子問題，即它的最優解可以從其子問題的最優解來有效地建構。滿足“将大問題分解為若幹個規模較小的問題”的條件。是以我們令 dp[n] 表示能到達第 n 階的方法總數，可以得到如下狀态轉移方程：

dp[n]=dp[n-1]+dp[n-2]

• 上 1 階台階：有1種方式。
• 上 2 階台階：有1+1和2兩種方式。
• 上 3 階台階：到達第3階的方法總數就是到第1階和第2階的方法數之和。
• 上 n 階台階，到達第n階的方法總數就是到第 (n-1) 階和第 (n-2) 階的方法數之和。

圖2

1.3 Go語言示例

根據分析，得到代碼如下：

func climbStairs(n int) int {
    if n == 1 {
        return 1
     }
     dp := make([]int, n+1)
     dp[1] = 1
     dp[2] = 2
     for i := 3; i <= n; i++ {
         dp[i] = dp[i-1] + dp[i-2]
    }
    return dp[n]
}           

動态規劃系列二：最大子序和

2.1 最大子序和

題目：給定一個整數數組 nums ，找到一個具有最大和的連續子數組（子數組最少包含一個元素），傳回其最大和。

示例 ：

輸入: [-2,1,-3,4,-1,2,1,-5,4],

輸出: 6

解釋: 連續子數組 [4,-1,2,1] 的和最大，為 6。

拿到題目請不要看下方題解，先自行思考2-3分鐘....

2.2 題目圖解

首先我們分析題目，一個連續子數組一定要以一個數作為結尾，那麼我們可以将狀态定義成如下：

dp[i]：表示以 nums[i] 結尾的連續子數組的最大和。

那麼為什麼這麼定義呢？因為這樣定義其實是最容易想到的！在上一節中我們提到，狀态轉移方程其實是通過1-3個參數的方程來描述小規模問題和大規模問題間的關系。

當然，如果你沒有想到，其實也非常正常！因為 "該問題最早于 1977 年提出，但是直到 1984 年才被發現了線性時間的最優解法。"

根據狀态的定義，我們繼續進行分析：

如果要得到dp[i]，那麼nums[i]一定會被選取。并且 dp[i] 所表示的連續子序列與 dp[i-1] 所表示的連續子序列很可能就差一個 nums[i] 。即

dp[i] = dp[i-1]+nums[i] , if (dp[i-1] >= 0)

但是這裡我們遇到一個問題，很有可能dp[i-1]本身是一個負數。那這種情況的話，如果dp[i]通過dp[i-1]+nums[i]來推導，那麼結果其實反而變小了，因為我們dp[i]要求的是最大和。是以在這種情況下，如果dp[i-1]<0，那麼dp[i]其實就是nums[i]的值。即

dp[i] = nums[i] , if (dp[i-1] < 0)

綜上分析，我們可以得到：

dp[i]=max(nums[i], dp[i−1]+nums[i])

得到了狀态轉移方程，但是我們還需要通過一個已有的狀态的進行推導，我們可以想到 dp[0] 一定是以 nums[0] 進行結尾，是以

dp[0] = nums[0]

在很多題目中，因為dp[i]本身就定義成了題目中的問題，是以dp[i]最終就是要的答案。但是這裡狀态中的定義，并不是題目中要的問題，不能直接傳回最後的一個狀态 (這一步經常有初學者會摔跟頭)。是以最終的答案，其實我們是尋找：

max(dp[0], dp[1], ..., d[i-1], dp[i])

分析完畢，我們繪制成圖：

假定 nums 為 [-2,1,-3,4,-1,2,1,-5,4]

圖3

2.3 Go語言示例

func maxSubArray(nums []int) int {
    if len(nums) < 1 {
        return 0
    }
    dp := make([]int, len(nums))
    //設定初始化值 
    dp[0] = nums[0]
    for i := 1; i < len(nums); i++ {
        //處理 dp[i-1] < 0 的情況
        if dp[i-1] < 0 {
            dp[i] = nums[i]
        } else {
            dp[i] = dp[i-1] + nums[i]
        }
    }
    result := -1 << 31
    for _, k := range dp {
        result = max(result, k)
    }
    return result
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}           

我們可以進一步精簡代碼為：

func maxSubArray(nums []int) int {
    if len(nums) < 1 {
        return 0
    }
    dp := make([]int, len(nums))
    result := nums[0]
    dp[0] = nums[0]
    for i := 1; i < len(nums); i++ {
        dp[i] = max(dp[i-1]+nums[i], nums[i])
        result = max(dp[i], result)
    }
    return result
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}           

複雜度分析：時間複雜度：O(N)。空間複雜度：O(N)。

動态規劃系列三：最長上升子序列

3.1 最長上升子序列

題目：給定一個無序的整數數組，找到其中最長上升子序列的長度。

示例:

輸入: [10,9,2,5,3,7,101,18]

輸出: 4

解釋: 最長的上升子序列是 [2,3,7,101]，它的長度是 4。

說明:可能會有多種最長上升子序列的組合，你隻需要輸出對應的長度即可。

本題有一定難度！

如果沒有思路請回顧上一篇的學習内容！

不建議直接看題解！

3.2 題目圖解

首先我們分析題目，要找的是最長上升子序列（Longest Increasing Subsequence，LIS）。因為題目中沒有要求連續，是以LIS可能是連續的，也可能是非連續的。同時，LIS符合可以從其子問題的最優解來進行建構的條件。是以我們可以嘗試用動态規劃來進行求解。首先我們定義狀态：

dp[i] ：表示以nums[i]結尾的最長上升子序列的長度

我們假定nums為[1，9，5，9，3]

圖4

我們分兩種情況進行讨論：

• 如果nums[i]比前面的所有元素都小，那麼dp[i]等于1（即它本身）（該結論正确）
• 如果nums[i]前面存在比他小的元素nums[j]，那麼dp[i]就等于dp[j]+1（該結論錯誤，比如nums[3]>nums[0]，即9>1,但是dp[3]并不等于dp[0]+1）

我們先初步得出上面的結論，但是我們發現了一些問題。因為dp[i]前面比他小的元素，不一定隻有一個！

可能除了nums[j]，還包括nums[k]，nums[p] 等等等等。是以dp[i]除了可能等于dp[j]+1，還有可能等于dp[k]+1，dp[p]+1 等等等等。是以我們求dp[i]，需要找到dp[j]+1，dp[k]+1，dp[p]+1 等等等等中的最大值。（我在3個等等等等上都進行了加粗，主要是因為初學者非常容易在這裡摔跟鬥！這裡強調的目的是希望能記住這道題型！）

即：

dp[i] = max(dp[j]+1，dp[k]+1，dp[p]+1，.....)

隻要滿足：

nums[i] > nums[j]

nums[i] > nums[k]

nums[i] > nums[p]

....

最後，我們隻需要找到dp數組中的最大值，就是我們要找的答案。

圖5

3.3 Go語言示例

func lengthOfLIS(nums []int) int {
    if len(nums) < 1 {
        return 0
    }
    dp := make([]int, len(nums))
    result := 1
    for i := 0; i < len(nums); i++ {
        dp[i] = 1
        for j := 0; j < i; j++ {
            //這行代碼就是上文中那個 等等等等
            if nums[j] < nums[i] {
                dp[i] = max(dp[j]+1, dp[i])
            }
        }
        result = max(result, dp[i])
    }
    return result
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}           

動态規劃系列四：三角形最小路徑和

前面章節我們通過題目“最長上升子序列”以及"最大子序和"，學習了DP（動态規劃）線上性關系中的分析方法。這種分析方法，也在運籌學中被稱為“線性動态規劃”，具體指的是 “目标函數為特定變量的線性函數，限制是這些變量的線性不等式或等式，目的是求目标函數的最大值或最小值”。這點大家作為了解即可，不需要死記，更不要生搬硬套！

在本節中，我們将繼續分析一道略微差別于之前的題型，希望可以由此題與之前的題目進行對比論證，進而順利求解！

4.1 三角形最小路徑和

題目：給定一個三角形，找出自頂向下的最小路徑和。

每一步隻能移動到下一行中相鄰的結點上。

例如，給定三角形：

自頂向下的最小路徑和為 11（即，2 + 3 + 5 + 1 = 11）。

4.2 自頂向下圖解分析

首先我們分析題目，要找的是三角形最小路徑和，這是個啥意思呢？假設我們有一個三角形：[[2], [3,4], [6,5,7], [4,1,8,3]]

圖6

那從上到下的最小路徑和就是2-3-5-1，等于11。

由于我們是使用數組來定義一個三角形，是以便于我們分析，我們将三角形稍微進行改動：

圖7

這樣相當于我們将整個三角形進行了拉伸。這時候，我們根據題目中給出的條件：每一步隻能移動到下一行中相鄰的結點上。其實也就等同于，每一步我們隻能往下移動一格或者右下移動一格。将其轉化成代碼，假如2所在的元素位置為[0,0]，那我們往下移動就隻能移動到[1,0]或者[1,1]的位置上。假如5所在的位置為[2,1]，同樣也隻能移動到[3,1]和[3,2]的位置上。如下圖所示：

圖8

題目明确了之後，現在我們開始進行分析。題目很明顯是一個找最優解的問題，并且可以從子問題的最優解進行建構。是以我們通過動态規劃進行求解。首先，我們定義狀态：

dpi : 表示包含第i行j列元素的最小路徑和

我們很容易想到可以自頂向下進行分析。并且，無論最後的路徑是哪一條，它一定要經過最頂上的元素，即[0,0]。是以我們需要對dp0進行初始化。

dp0 = 0位置所在的元素值

繼續分析，如果我們要求dpi，那麼其一定會從自己頭頂上的兩個元素移動而來。

圖9

如5這個位置的最小路徑和，要麼是從2-3-5而來，要麼是從2-4-5而來。然後取兩條路徑和中較小的一個即可。進而我們得到狀态轉移方程：

dpi = min(dpi-1,dpi-1) + trianglei

但是，我們這裡會遇到一個問題！除了最頂上的元素之外，

圖10

最左邊的元素隻能從自己頭頂而來。（2-3-6-4）

圖11

最右邊的元素隻能從自己左上角而來。（2-4-7-3）

然後，我們觀察發現，位于第2行的元素，都是特殊元素（因為都隻能從[0,0]的元素走過來）

圖12

我們可以直接将其特殊處理，得到：

dp1 = triangle1 + triangle0

最後，我們隻要找到最後一行元素中，路徑和最小的一個，就是我們的答案。即：

l：dp數組長度

result = min(dp[l-1,0]，dp[l-1,1]，dp[l-1,2]....)

綜上我們就分析完了，我們總共進行了4步：

• 定義狀态
• 總結狀态轉移方程
• 分析狀态轉移方程不能滿足的特殊情況。
• 得到最終解

4.3 代碼分析

分析完畢，代碼自成：

func minimumTotal(triangle [][]int) int {
    if len(triangle) < 1 {
        return 0
    }
    if len(triangle) == 1 {
        return triangle[0][0]
    }
    dp := make([][]int, len(triangle))
    for i, arr := range triangle {
        dp[i] = make([]int, len(arr))
    }
    result := 1<<31 - 1
    dp[0][0] = triangle[0][0]
    dp[1][1] = triangle[1][1] + triangle[0][0]
    dp[1][0] = triangle[1][0] + triangle[0][0]
    for i := 2; i < len(triangle); i++ {
        for j := 0; j < len(triangle[i]); j++ {
            if j == 0 {
                dp[i][j] = dp[i-1][j] + triangle[i][j]
            } else if j == (len(triangle[i]) - 1) {
                dp[i][j] = dp[i-1][j-1] + triangle[i][j]
            } else {
                dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]
            }
        }  
    }
    for _,k := range dp[len(dp)-1] {
        result = min(result, k)
    }
    return result
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}           

圖13

運作上面的代碼，我們發現使用的記憶體過大。我們有沒有什麼辦法可以壓縮記憶體呢？通過觀察我們發現，在我們自頂向下的過程中，其實我們隻需要使用到上一層中已經累積計算完畢的資料，并且不會再次通路之前的元素資料。繪制成圖如下：

圖14

優化後的代碼如下：

func minimumTotal(triangle [][]int) int {
    l := len(triangle)
    if l < 1 {
        return 0
    }
    if l == 1 {
        return triangle[0][0]
    }
    result := 1<<31 - 1
    triangle[0][0] = triangle[0][0]
    triangle[1][1] = triangle[1][1] + triangle[0][0]
    triangle[1][0] = triangle[1][0] + triangle[0][0]
    for i := 2; i < l; i++ {
        for j := 0; j < len(triangle[i]); j++ {
            if j == 0 {
                triangle[i][j] = triangle[i-1][j] + triangle[i][j]
            } else if j == (len(triangle[i]) - 1) {
                triangle[i][j] = triangle[i-1][j-1] + triangle[i][j]
            } else {
                triangle[i][j] = min(triangle[i-1][j-1], triangle[i-1][j]) + triangle[i][j]
            }
        }  
    }
    for _,k := range triangle[l-1] {
        result = min(result, k)
    }
    return result
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}           

圖15

動态規劃系列五：最小路徑和

在上節中，我們通過分析，順利完成了“三角形最小路徑和”的動态規劃題解。在本節中，我們繼續看一道相似題型，以求能完全掌握這種“路徑和”的問題。話不多說，先看題目：

5.1 最小路徑和

題目：給定一個包含非負整數的 m x n 網格，請找出一條從左上角到右下角的路徑，使得路徑上的數字總和為最小。說明：每次隻能向下或者向右移動一步。

輸入:

[

[1,3,1],

[1,5,1],

[4,2,1]

]

輸出: 7

解釋: 因為路徑 1→3→1→1→1 的總和最小。

5.2 圖解分析

首先我們分析題目，要找的是 最小路徑和，這是個啥意思呢？假設我們有一個 m*n 的矩形 ：[[1,3,1],[1,5,1],[4,2,1]]

圖16

那從左上角到右下角的最小路徑和，我們可以很容易看出就是1-3-1-1-1，這一條路徑，結果等于7。

題目明确了，我們繼續進行分析。該題與上一道求三角形最小路徑和一樣，題目明顯符合可以從子問題的最優解進行建構，是以我們考慮使用動态規劃進行求解。首先，我們定義狀态：

同樣，因為任何一條到達右下角的路徑，都會經過[0,0]這個元素。是以我們需要對dp0進行初始化。

繼續分析，根據題目給的條件，如果我們要求dpi，那麼它一定是從自己的上方或者左邊移動而來。如下圖所示：

圖17

• 5，隻能從3或者1移動而來
• 2，隻能從5或者4移動而來
• 4，從1移動而來
• 3，從1移動而來
• 紅色位置必須從藍色位置移動而來

進而我們得到狀态轉移方程：

dpi = min(dpi-1,dpi) + gridi

同樣我們需要考慮兩種特殊情況：

• 最上面一行，隻能由左邊移動而來（1-3-1）
• 最左邊一列，隻能由上面移動而來（1-1-4）

圖18

最後，因為我們的目标是從左上角走到右下角，整個網格的最小路徑和其實就是包含右下角元素的最小路徑和。即：

設：dp的長度為l

最終結果就是：dpl-1)-1]

5.3 代碼分析

func minPathSum(grid [][]int) int {
    l := len(grid)
    if l < 1 {
        return 0
    }
    dp := make([][]int, l)
    for i, arr := range grid {
        dp[i] = make([]int, len(arr))
    }
    dp[0][0] = grid[0][0]
    for i := 0; i < l; i++ {
        for j := 0; j < len(grid[i]); j++ {
            if i == 0 && j != 0 {
                dp[i][j] = dp[i][j-1] + grid[i][j]
            } else if j == 0 && i != 0 {
                dp[i][j] = dp[i-1][j] + grid[i][j]
            } else if i != 0 && j != 0 {
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
            }
        }
    }
    return dp[l-1][len(dp[l-1])-1]
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}           

圖19

同樣，運作上面的代碼，我們發現使用的記憶體過大。有沒有什麼辦法可以壓縮記憶體呢？通過觀察我們發現，在我們自左上角到右下角計算各個節點的最小路徑和的過程中，我們隻需要使用到之前已經累積計算完畢的資料，并且不會再次通路之前的元素資料。繪制成圖如下：(大家看這個過程像不像掃雷，其實如果大家研究掃雷外挂的話，就會發現在掃雷的核心算法中，就有一處頗為類似這種分析方法，這裡就不深究了)

圖20

func minPathSum(grid [][]int) int {
    l := len(grid)
    if l < 1 {
        return 0
    }
    for i := 0; i < l; i++ {
        for j := 0; j < len(grid[i]); j++ {
            if i == 0 && j != 0 {
                grid[i][j] = grid[i][j-1] + grid[i][j]
            } else if j == 0 && i != 0 {
                grid[i][j] = grid[i-1][j] + grid[i][j]
            } else if i != 0 && j != 0 {
                grid[i][j] = min(grid[i-1][j], grid[i][j-1]) + grid[i][j]
            }
        }
    }
    return grid[l-1][len(grid[l-1])-1]
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}           

圖21

本系列所有教程中都不會用到複雜的語言特性，大家不需要擔心沒有學過go。算法思想最重要，使用go純屬作者愛好。

原文首發于公衆号-浩仔講算法

小浩：宜信科技中心攻城獅一枚，熱愛算法，熱愛學習，不拘泥于枯燥程式設計代碼，更喜歡用輕松方式把問題簡單闡述，希望喜歡的小夥伴可以多多關注！