Python算法題解：動态規劃解0-1背包問題

概述

背包問題（Knapsack problem）是一種組合優化的NP完全問題。問題可以描述為：給定一組物品，每種物品都有自己的重量和價格，在限定的總重量内，我們如何選擇，才能使得物品的總價格最高。問題的名稱來源于如何選擇最合适的物品放置于給定背包中。

定義

我們有 n 種物品，物品 j 的重量為wj，價格為pj。

我們假定所有物品的重量和價格都是非負的。背包所能承受的最大重量為W。

如果限定每種物品隻能選擇0個或1個，則問題稱為0-1背包問題。

如果限定物品j最多隻能選擇bj個，則問題稱為有界背包問題。

如果不限定每種物品的數量，則問題稱為無界背包問題。

動态規劃

動态規劃背後的基本思想非常簡單。大緻上，若要解一個給定問題，我們需要解其不同部分（即子問題），再根據子問題的解以得出原問題的解。

通常許多子問題非常相似，為此動态規劃法試圖僅僅解決每個子問題一次，進而減少計算量：一旦某個給定子問題的解已經算出，則将其記憶化存儲，以便下次需要同一個子問題解之時直接查表。

思路

舉例，令物品數量N=5，背包所能承受的最大重量為W=10，物品與價格的對應關系如下表左三列所示。

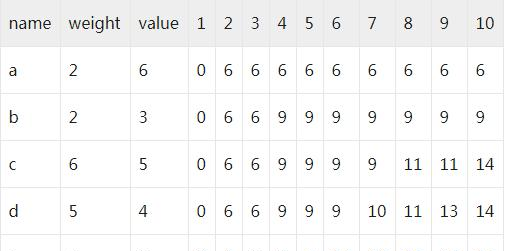
當放入物品a時，在背包所能承受的重量内，計算背包擁有的物品總價格，并進行标記，如表格第一行所示，當背包所能承受的重量大于等于2時，都可以放入物品a，背包擁有的物品總價格為6。

接着我們放入物品b，放入之前，一是要判斷背包是否所能承受其重量，二是判斷放入之後與放入之前擁有的物品總價格哪個最大，如表格第二行所示，當背包所能承受的重量大于等于2時，都可以放入物品b，但是，物品b在背包容量為[2,3]的時候，放入之後的總價格3不如放入之前的總價格6大，是以不放入。

當背包所能承受的重量等于4時，放入物品b後，背包所能承受的重量4減去物品b的重量2後，剩餘的所能承受的重量2還可以放入物品a，此時背包擁有的物品總價格為物品a和物品b的總價格之和，即為9，大于放入之前的物品總價格6，是以此時背包擁有的物品總價格最大為9。

分析可知，在一層循環周遊下，我們需要一個一維數組儲存背包所能承受的最大重量與其擁有的物品總價格，并不斷更新。

代碼

Copy/0-1背包問題@paramN物品數量@paramW背包容量@paramweight物品重量@paramvalue物品價格@return最大價值/privatestaticinttraceBack(intN,intW,int[]weight,int[]value){int[]dp=newint[W+1];//範圍[0,W]目前背包容量對應的物品總價值for(inti=0;i=weight[i];j--){//隻要背包可以放入就放dp[j]=Math.max(dp[j-weight[i]]+value[i],dp[j]);//比較放入物品之前與放入之後的價值哪個大}}returndp[W];}

複雜度

顯而易見，算法需要的時間複雜度為O(nW)，空間的消耗（即所需的一維數組）為O(W)。

有不清楚的地方，夥伴們可以留言，更多的Python相關教程也會繼續為大家更新！