分類回歸樹 CART 是決策樹家族中的基礎算法,它非常直覺(intuitive),但看網上的文章,很少能把它講的通俗易懂(也許是我了解能力不夠),幸運的是,我在 Youtube 上看到了 這個視訊 ,可以讓你在沒有任何機器學習基礎的情況下掌握 CART 的原理,下面我嘗試着把它寫出來,以加深印象.
決策樹的結構
下圖是一個簡單的決策樹示例:
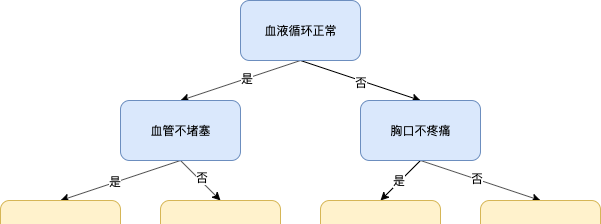
假設上面這個決策樹是一個用來判斷病人是否患有心髒病的系統,當病人前來就醫時,系統首先會問他:血液循環是否正常?此時如果病人回答是,系統會走左邊的分支,并繼續問:血管是否不堵塞?如果此時病人回答是,系統便會判斷該病人沒有患心髒病,反之則會判斷他患有心髒病。同理,如果病人的第一個問題的回答是否,則決策樹會走到右邊的分支,接下來會繼續後面的提問,直到來到樹的根部,以輸出結果。
可見,決策樹是一個二叉樹結構的模型,它可以被用來解決分類問題或回歸問題,該樹的非葉子節點本質上是一些條件表達式,用來決定樹根到葉子的路徑,而葉子節點便是該模型的預測結果。
本文主要介紹如何建構一棵分類樹:
如何建構一棵分類樹
在構造這棵“判斷心髒病的決策樹”之前,我們有一堆病人的診斷資料,如下
| 胸口疼痛 | 血液循環正常 | 血管堵塞 | 患有心髒病 |
|---|---|---|---|
| 否 | |||
| 是 | |||
| ... |
剛開始,我們可以使用「胸口疼痛」或者「血液循環正常」或者「血管堵塞」這三個特征中的一個來作為樹根,但這樣做會存在一個問題:任何上述特征都無法将是否患有心髒病分類得完全正确,如下:
既然沒有絕對最優的答案,我們一般會選擇一個相對最優的答案,即在這 3 個特征中選擇一個相對最好的特征作為樹根,如何衡量它們的分類好壞呢?我們可以使用不純度(impurity)這個名額來度量,例如下圖中,P1(藍色機率分布)相對于 P2(橙色機率分布) 來說就是不純的。對于一個節點的分類結果來說(上圖黃色節點),當然希望它的分布越純越好。
計算一個分布的不純度有很多方法,這裡使用的是基尼系數(Gini coefficient)——基尼系數越高,越不純,反之越純。計算基尼系數的公式很簡單:
$$
Gini = 1 - \sum_{i=1}^n p_i^2
這裡 $p_i$ 表示離散機率分布中的機率值,我們來算一下上圖中 P1 和 P2 的基尼系數
Gini(P1) = 1 - 5 \times 0.2^2 = 0.8
Gini(P2) = 1 - 1^2 - 4 \times 0^2 = 0
可見 P1 的基尼系數更高,其更不純。
有了以上基礎,接下來我們就可以依次計算不同特征分類的基尼不純度,從中選一個值最低的特征來作為樹根,以「胸口疼痛」特征為例,其左邊和右邊的分類結果的基尼不純度為:
G(ChestPain_Y) = 1 - (\frac{105}{105+39})^2 - (\frac{39}{105+39})^2 = 0.395
G(ChestPain_N) = 1 - (\frac{34}{34+127})^2 - (\frac{127}{34+127})^2 = 0.336
那麼,「胸口疼痛」這個節點整體的不純度則為左右兩個不純度的權重平均,如下:
G(ChestPain) = \frac{105+39}{105+39+34+125} \times 0.395 + \frac{34+125}{105+39+34+125} \times 0.336 = 0.364
同理,我們也可以計算出「血液循環正常」和「血管堵塞」的基尼不純度分别為 0.360 和 0.381。相比之下,「血液循環正常」的值最小,該特征便是我們的樹根。
在選出了樹根後,原來的一份資料被樹根分成了兩份,後續要做的事情相信很多同學已經猜到了:對于新産生的兩份資料,每份資料再使用同樣的方法,使用剩下的特征來産生非葉子節點,如此遞歸下去,直到滿足下面兩個條件中的任意一條:
- 每條路徑上所有特征都使用過
- 使用新特征沒有使分類結果更好(此時不産生新的節點)
上述第 1 個條件很容易了解,我們一起來看下第 2 個條件,假設在建樹的過程中,其中一條路徑如下:
現在我們需要決定黃色的這部分資料是否還需要被「胸口疼痛」這個特征分類,假設用「胸口疼痛」來分類該資料的結果如下:
接下來我們就要對分類前後做效果對比,依然計算它們的基尼不純度,在分類前,基尼不純度為:
G(before) = 1-(\frac{102}{102+13})^2 -(\frac{13}{102+13})^2 = 0.201
而使用「胸口疼痛」分類之後,基尼不純度為(省去計算細節):
G(ChestPain) = 0.286
顯然繼續分類隻會使結果更糟,是以該分支的建立提前結束了,且分支上隻有「血液循環正常」和「血管堵塞」這兩個特征來進行分類。
值得一提的是,在建樹過程中,即便候選節點的基尼不純度更低,但如果該名額的降低不能超過一定的門檻值,也不建議繼續加節點,這種做法可以在一定程度上緩解過拟合的問題。例如:假設該門檻值設定為0.05,即便 G(胸口疼痛) 為 0.16,也不繼續将「胸口疼痛」作為該分支上的一個節點用來分類,因為此時基尼不純度隻降低了 0.04,低于門檻值 0.05。
如何處理離散型資料
上面例子中的資料是隻有 0 或者 1 的布爾類型的資料,如果遇到其他類型的資料該怎麼處理呢?先來看一下離散型資料,這種類型的資料需要考慮 2 種情況:
- 有順序的離散型資料,例如電商網站把商品的評論分為:好評、中評和差評
- 順序無關的離散型資料,例如商品可能的顔色有:紅色、黃色和藍色
有順序的離散型資料
假如我們有以下資料,它根據使用者對商品的評價來判斷使用者是否喜歡該商品,其中,對商品的評價被編碼為 1(差評)、2(中評) 和 3(好評):
| 商品評價 | 是否喜歡 |
|---|---|
| 1 | |
| 3 | |
| 2 | |
以上問題實際上等價于選擇一個評價值,它能夠更好的把人們的喜好分開,這個值可以是 1 或者 2,即當商品評價“小于等于1”或者“小于等于2”時,判斷使用者不喜歡它,否則為喜歡它,這裡沒有“小于等于3”這個選項,因為該選項會包含所有的資料,沒有分類價值;于是,根據上述兩個選項,我們可以對資料做如下 2 種分類:
接下來分别計算它們的基尼不純度,其中左邊的結果 G(1) = 0.486,而右邊 G(2) = 0.476;于是,當使用「商品評價」這個特征來做分類時,該特征的切分點(cutoff)為“小于等于2”。
順序無關的離散型資料
我們再來看一個根據商品的顔色來判斷使用者是否喜歡該商品的例子,有如下資料:
| 商品顔色 | |
|---|---|
| RED | |
| YELLOW | |
| BLUE | |
對于以上資料,其作為節點的判斷條件有以下 6 種可能:
- 紅色表示喜歡
- 黃色表示喜歡
- 藍色表示喜歡
- 紅色或黃色表示喜歡
- 紅色或藍色表示喜歡
- 黃色或藍色表示喜歡
類似的,我們對每一種可能的分類結果計算其基尼不純度,然後再選擇最低的那個值對應的條件。
如何處理連續型資料
最後我們再來看看特征是連續型資料的情況,例如我們通過人的身高來判斷是否患有心髒病,資料如下:
| 身高 | |
|---|---|
| 220 | |
| 180 | |
| 225 | |
| 155 | |
| 190 |
處理這類資料的思路和上面幾種做法一緻,也就是尋找一個使基尼不純度最低的 cutoff。具體步驟是,先對身高進行排序,然後求相鄰兩個資料之間的平均值,以每個平均值作為分界點,對目标資料進行分類,并計算它們的基尼不純度,如下:
| 相鄰平均值 | 基尼不純度 | |
|---|---|---|
| 222.5 | 0.4 | |
| 205 | 0.27 | |
| 185 | 0.47 | |
| 167.5 | 0.3 | |
是以,在使用「身高」來建樹時,其切分點為 205,即”小于205”被判斷為未患心髒病,而”不小于205“的會被診斷為患病。
總結
本文主要介紹了 CART 中的分類樹的建構算法原理,及遇到了不同類型的資料時,該算法會如何處理。
參考:StatQuest: Decision Trees (
http://1t.click/aMGq)