的基礎之上,我們可以很容易的掌握随機森林算法,它們之間的差別在于,CART 決策樹較容易過拟合,而随機森林可以在一定程度上解決該問題。
随機森林的主要思想是:使用随機性産生出一系列簡單的決策樹,并組合它們的預測結果為最終的結果,可謂三個臭皮匠賽過一個諸葛亮,下面我們就來具體了解一下。
産生随機森林的具體步驟
産生随機森林的步驟大緻為三步
- 準備樣本
- 産生決策樹
- 循環第 1 、2 步,直到産生足夠的決策樹,一般為上百個
在第 1 步,它是一個可放回抽樣,即所産生的樣本是允許重複的,這種抽樣又被稱為 Bootstrap,例如我們有以下 dummy 資料
| 胸口疼痛 | 血液循環正常 | 血管堵塞 | 體重 | 患心髒病 |
|---|---|---|---|---|
| No | 125 | |||
| Yes | 180 | |||
| 210 | ||||
| 167 |
在做完 Bootstrap 之後,可能的樣本資料如下
可見,樣本資料中,第 3 條和第 4 條樣本是一樣的,都對應的是原始資料中的第 4 條。
接下來,就是要使用上面的樣本資料來産生決策樹了,産生決策樹的方法和 CART 基本一緻,唯一的不同地方在于,節點的建構不是來自于全部的候選特征,而是先從中随機的選擇 n 個特征,在這 n 個特征中找出一個作為最佳節點。
舉個例子,假設 n = 2,且我們随機選擇了「血液循環正常」和「血管堵塞」這兩個特征來産生根節點,如下:
我們将在上述兩個特征中選擇一個合适的特征作為根節點,假設在計算完 Gini 不純度之後,「血液循環正常」這個特征勝出,那麼我們的根節點便是「血液循環正常」,如下圖所示
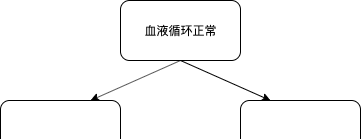
接下來我們還需要建構根節點下面的節點,下一個節點将會在剩下的「胸口疼痛」、「血管堵塞」和「體重」三個特征中産生,但我們依然不會計算所有這 3 個特征的 Gini 不純度,而是從中随機選擇 2 個特征,取這 2 個特征中的 Gini 不純度較低者作為節點。
例如我們随機選到了「胸口疼痛」和「體重」這兩列,如下:
假設此時「體重」的 Gini 不純度更低,那麼第 2 個節點便是「體重」,如下圖:
繼續下去,我們便産生了一棵決策樹。
随機森林是多棵決策樹,在産生完一棵決策樹後,接着會循環執行上述過程:Bootstrap 出訓練樣本,訓練決策樹,直到樹的數量達到設定值——通常為幾百棵樹。
随機森林的預測
現在我們産生了幾百棵樹的随機森林,當我們要預測一條資料時,該怎麼做呢?我們會聚合這些樹的結果,選擇預測結果最多的那個分類作為最終的預測結果。
例如我們現在有一條資料:
| 168 |
該條資料被所有樹預測的結果如下:
| 第幾顆樹 | 預測結果 |
|---|---|
| 1 | |
| 2 | |
| ... | |
| 100 |
上述結果聚合後為:
| 次數 | |
|---|---|
| 82 | |
| 18 |
取最多的那項為最終的預測結果,即 Yes——該病人被診斷為患有心髒病。
以上,随機森林的兩個過程:Bootstrap 和 Aggregate 又被稱為 Bagging。
總結
本文我們一起學習了随機森林的算法,和 CART 決策樹比起來,它主要被用來解決過拟合問題,其主要的思想為 Bagging,即随機性有助于增強模型的泛化(Variance) 能力。
參考:
相關文章: