本小節的示例比較簡單,因為在每次遞歸過程中原問題僅縮減為單個更小的問題。這樣的問題往往能夠用簡單循環解決。這類遞歸算法的函數調用圖是鍊狀結構。這種遞歸類型被稱為“單重遞歸”(single recursion)。
示例一:編寫函數seq(n),列印從1到n的數字。
可以很容易地用循環解決這個問題:
def seq(n):
i = 1
while i<=n:
print(i)
i += 1 也可以使用遞歸版本,這是本節的主要程式風格:
def seq(n):
if n>0:
seq(n-1)
print(n) 在遞歸版本的seq()函數中,參數等于0時函數什麼也不做直接傳回。當參數為正整數時[1],将參數減1後調用自身,待調用傳回後列印參數。當調用seq(3)時,該函數會生成如下的調用鍊seq(3) > seq(2) > seq(1) > seq(0),當調用鍊依次傳回時,seq(3) - seq(1)的print語句會逆序執行,完成列印序列的目的。如圖 2.10所示。
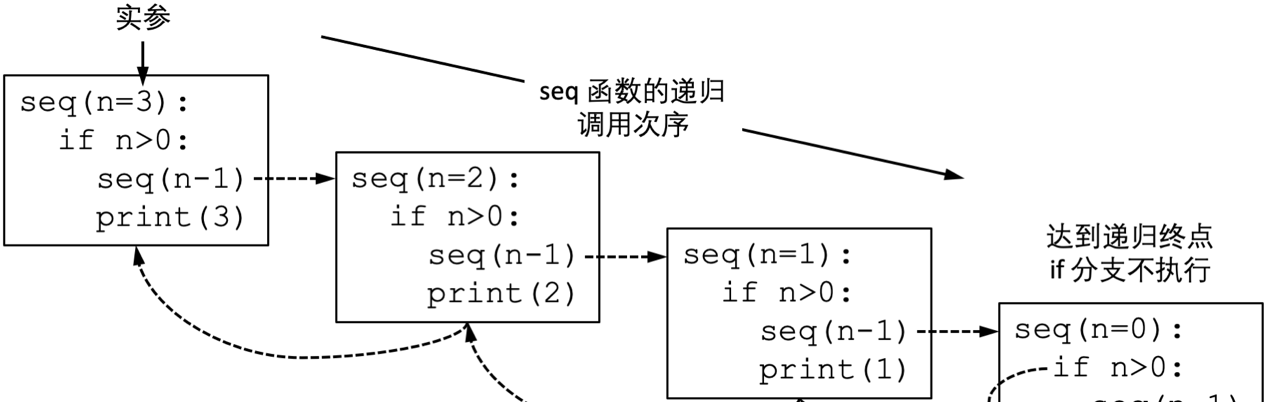
圖 2.10 seq函數的遞歸調用次序
圖 2.11 seq的調用棧變化示意圖
在實際編寫代碼時,不會使用這樣的方式列印序列[2]。因為對于本問題來說,遞歸版本的效率很低。本小節示例的目的是讓讀者了解遞歸函數的執行流程和基本文法形式。
[1] 為了簡單起見,假定函數隻會接收到非負整數作為參數。
[2] 據傳這是世紀之交某跨國大型IT企業的應屆生招聘試題。原題是“編寫函數,不使用局部變量列印1到n”。當時的很多畢業生對此束手無策。從這個角度上該問題的遞歸版本還是有意義的。時至今日這已是平常技巧,已不常見于企業面試題。
這是一本很有趣很有趣的Python入門書,牆裂推薦。