前面兩篇部落格介紹了線性表的順序存儲與鍊式存儲以及對應的操作,并且還聊了棧與隊列的相關内容。本篇部落格我們就繼續聊資料結構的相關東西,并且所涉及的相關Demo依然使用面向對象語言Swift來表示。本篇部落格我們就來介紹樹結構的一種:二叉樹。在之前的部落格中我們簡單的聊了一點樹的東西,樹結構的特點是除頭節點以外的節點隻有一個前驅,但是可以有一個或者多個後繼。而二叉樹的特點是除頭結點外的其他節點隻有一個前驅,節點的後繼不能超過2個。
本篇部落格,我們隻對二叉樹進行讨論。在本篇部落格中,我們對二叉樹進行建立,然後進行各種周遊,最後将二叉樹進行線索化。在Demo實作之前,我們先對二叉樹的概念及其特性進行介紹,然後在給出具體的代碼實作。
一、二叉樹的特性
上面我們已經提到過,一個除頭結點外,每個節點隻有一個前驅,有零到兩個後繼的樹即為二叉樹。在二叉樹中,一個節點可以有左節點或者左子樹,也可以有右節點或者右子樹。一些特殊的二叉樹,比如斜二叉樹、滿二叉樹、完全二叉樹等等就不做過多贅述了。說這麼多,不如看一張圖來的直覺。下方就是一個典型的二叉樹。
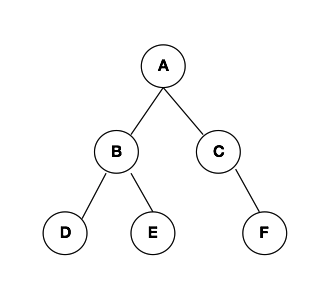
- 特性1:在二叉樹的第i層上至多有2^(i-1)(i >= 1)個節點。
- 這一特性比較好了解,如果層數是從零開始數的話,那麼低i層上的節點數就是2^i,因為二叉樹層與層之間的節點數是以2的指數幂進行增長的。如果根節點算是第0層的話,那麼第n層的節點數就是2^n次幂。
- 特性2:深度為k的二叉樹至多有2^k-1(k>=1)個節點。
- 這一特性也是比較好了解的, 由數學上的遞加公式就可以很容易的推出來。由特性1易知每層最多有多少個節點,那麼深度為k的話,說明一共有k層,那麼共有節點數為:2^0 + 2^1 + 2^2 + 2^(k-1) = 2^k - 1。
- 特性3:二叉樹的葉子節點數為n0, 度為2的節點數為n2, 那麼n0 = n2 + 1。
- 這一特性也不難了解,推出n0 = n2 + 1這個公式并不難。我們假設葉子節點,也就是度數為0的節點的個數為n0, 度數為1的節點為n1, 度數為2的節點n2。那麼二叉樹的節點總數 n = n0 + n1 + n2。因為除了根節點外其餘的節點入度都為1,是以二叉樹的度數為n-1,當然度的個數可以使用出度來算,即為2*n2+n1,是以n-1=2*n2+n1。以n=n0+n1+n2與n-1=2*n2+n1這兩個公式我們很容易的推出n0 = n2 + 1。
- 特性4:具有n個結點的完全二叉樹的深度為log2n + 1 (向下取整,比如3.5,就取3)。
- 這個特性也是比較好了解的,基于完全二叉樹的特點,我們假設完全二叉樹的深度為k, 那麼二叉樹的結點個數的範圍為2(k-1)-1 <= n <= 2k-1。由這個表達式我們很容易推出特性4。
二、二叉樹的建立
上面介紹完二叉樹的特性後,接下來我們要做的就是将二叉樹進行存儲。當然一般存儲二叉樹的結構是以二叉連結清單的形式來存儲的。二叉連結清單的結構類似于雙向連結清單,二叉連結清單的節點也是有兩個結點指針的,一個指向左子樹,一個指向右子樹。接下來我們要使用二叉連結清單的形式來存儲我們的二叉樹。
1.先序建立二叉樹
在建立二叉樹之前,我們先了解一個什麼是先序周遊。先序周遊就是先周遊根結點,然後周遊左子樹,最後周遊右子樹。我們就以此規則來建立二叉樹,換句話說,我們有一個資料序列,将依照這個序列按照先序建立二叉樹的原則來建立該二叉樹,先建立二叉樹的根節點,然後再建立二叉樹的左子樹,然後再建立右子樹。而這個建立的二叉樹的先序周遊的結果就是我們之前輸入的資料序列。下方就是先序建立二叉樹的原理圖。
從上面的分析我們不難看出,我們要先建立根節點,然後建立左子樹,最後建立右子樹。因為左子樹和右子樹都是二叉樹,是以建立左子樹和右子樹是原問題的子問題。也就是說子問題與原問題解決方案一緻,這種情況下就可以使用遞歸的思想來解決。我們先将上述二叉樹的結構轉換成二叉連結清單的形式直覺的感受一下,然後再将其使用代碼的形式進行表示即可。下方這個截圖就是上述二叉樹的二叉連結清單的存儲結構。每個節點都有左指針與右指針,分别自己的左子節點和右子節點。如果沒有子節點就為空。
2.先序建立二叉樹的代碼實作
上面我們分析了二叉連結清單的結構,接下來我們就來建立二叉連結清單了。首先我們得建立二叉連結清單的節點類,之前我們用C語言來實作二叉樹的時候,是使用的結構體來實作的二叉連結清單的節點,因為C語言是面向過程的語言,根本就沒有類這個概念。因為此刻我們是使用的面向對象語言,是以我就可以使用一個類來表示我們二叉連結清單的節點了。下方這個GeneralBinaryTreeNote就是二叉連結清單的類。data屬性存儲的就是樹節點中所存儲的值,而leftChild就指向左節點的記憶體位址,而rightChild就指向右節點的記憶體位址。
上面我們已經說過,先序建立二叉樹的過程是可以用遞歸來表示的,是以我們就遞歸的去建立我們想要建立的二叉樹。下方就是先序建立二叉樹的核心代碼,self.items中存儲的是二叉樹的節點資訊。經過下方函數的遞歸執行,就可以建立出我們想要的二叉樹了。從下方的遞歸過程我們就明顯的能看出是先序建立的二叉樹。先建立的根節點,然後遞歸建立左子樹,然後在遞歸建立右子樹。
下方就是我們二叉樹的初始化過程,下方在初始化過程中主要是調用上方的這個方法,将items數組中存儲的值轉換成二叉連結清單的存儲結構。items數組中的空字元串,表明該節點為空。
其實上面執行個體中所建立的二叉樹的結構就是下方的結構。
三、二叉樹的周遊
聊二叉樹怎麼能沒有二叉樹的周遊呢,下方就會給出幾種常見的二叉樹的周遊方法。在周遊二叉樹的方法中一般有先序周遊,中序周遊,後續周遊,層次周遊。本篇部落客要給出前三種周遊方式,而層次周遊會在圖的部分進行介紹。二叉樹的層次周遊其實與圖的廣度搜尋是一樣的,是以這部分放到圖的相關部落格中介紹。下方會給出幾種周遊的具體方式,然後給出具體的代碼實作。
二叉樹的先、中、後周遊,這個先中後指的是周遊根節點的先後順序。先序周遊:根左右,中序周遊:左根右,後序周遊:左右根。下方将詳細介紹到。
1.先序周遊
關于先序周遊,上面已經介紹過一些了,接下來再進行細化一下。先序周遊,就是先周遊根節點然後再周遊左子樹,最後周遊右子樹。下圖就是我們上面建立的二叉樹的先序周遊的順序,由下方的示例圖就可以看出先序周遊的規則。一句話總結下方的結構圖:根節點->左節點->右節點。下方先序周遊的順序為:A B D 空 空 E 空 空 C 空 F 空 空 。
上面給出了原理,接下來又到了代碼實作的時候了。在樹的周遊時,我們依然是采用遞歸的方式,因為無論是左子樹還是右子樹,都是二叉樹的範疇。是以在進行二叉樹周遊時,可以使用遞歸周遊的形式。而先序周遊莫非就是先周遊根節點,然後遞歸周遊左子樹,最後周遊右子樹。下方就是先序周遊的代碼實作。在下方代碼中,如果左節點或者右節點為空,那麼我們就輸出“空”。
2.中序周遊
中序周遊,與先序周遊的不同之處在于,中序周遊是先周遊左子樹,然後周遊根節點,最後周遊右子樹。一句話總結:左子樹->根節點->右子樹。下方就是我們之前建立的樹的中序周遊的結構圖以及中序周遊的結果。
中序周遊的代碼實作與先序周遊的代碼實作類似,都是使用遞歸的方式來實作的,隻不過是先遞歸周遊左子樹,然後周遊根節點,最後周遊右子樹。下方就是中序周遊的代碼具體實作。
3.後序周遊
接下來聊一下二叉樹的後序周遊。如果上面這兩種周遊方式了解的話,那麼後序周遊也是比較好了解的。後序周遊是先周遊左子樹,然後再周遊右子樹,最後周遊根節點。與上方的表示方法一直,首先我們給出表示圖,如下所示:
後序周遊的代碼就不做過多贅述了,與之前兩種依然類似,隻是換了一下周遊的順序。下方就是二叉樹後序周遊的代碼實作。
4、層次周遊
二叉樹的層次周遊就不是二叉樹這種資料結構所獨有的了。後面的部落格中我們會介紹到圖這種資料結構,在圖中有一個廣度搜尋,放到二叉樹中就是層次周遊。也就是說二叉樹的層次周遊,就是圖中以二叉樹的根節點為起始節點的廣度搜尋(BFS)。本篇部落格就不給出具體的代碼了,後面的部落格會給出BFS的具體算法。當然在之前的部落格中有圖的BFS以及DFS。不過是C語言的實作。下方就是二叉樹層次周遊的執行個體圖。
四、二叉樹的線索化
二叉樹的線索化,起始就是利用二叉樹中的空的節點來将二叉樹轉換成連結清單的結構。當然隻針對中序周遊的序列。從上面中序周遊的結果中,我們不難看出,有節點的值與空指針是間隔的(空 D 空 B 空 E 空 A 空 C 空 F 空)。也就是說好多空的左指針與右指針浪費了。二叉樹的線索化,就是在中序周遊中,将空的左子樹的指針指向其中序周遊結果的前驅,而空的右子樹指針指向中序周遊中該節點的後繼。具體的示意圖如下所示:
從上面的圖中我們不難看出。在被線索化的二叉樹中,左節點指針不止指向左節點,而且有可能指向節點的前驅。而右節點指針不僅僅是指向右節點的指針,還有可能指向該節點在中序周遊中的後繼節點。為了标記指針是指向子節點還是指向前驅或者後繼,是以我們要添加相應的标志位來标記指針指向的是那些節點。下方就是我們改造後的二叉樹的節點:
改造完節點後,我們就可以将二叉樹進行線索化了,下方就是被線索話的二叉樹的代碼。可以看出,下方的代碼的整體步驟與二叉樹的中序周遊類似。
被線索化的二叉樹就可以根據我們添加的線索進行中序周遊了,效率要比遞歸的中序周遊要高的多,如下所示:
五、測試用例
上面的代碼都是如何去實作了,接下來到了我們測試的時間了,下方這段代碼段是我們的測試用例。首先給出二叉樹的節點資訊,然後先序的建立一棵二叉樹。然後給出二叉樹的先、中、後續周遊,最後給出二叉樹線索話的結果。
下方截圖就是我們測試用例的運作結果,一目了然,在此就不做過多的贅述了。
本篇部落格的篇幅也夠長的了,就先到這兒吧,上述執行個體的完整Demo會在github上進行分享, 下篇部落格我們将要介紹圖的鄰接連結清單和鄰接矩陣,以及圖的BFS和DFS。
github連結位址:https://github.com/lizelu/DataStruct-Swift/tree/master/BinaryTree
作者:青玉伏案
出處:http://www.cnblogs.com/ludashi/
本文版權歸作者和共部落格園共有,歡迎轉載,但未經作者同意必須保留此段聲明,且在文章頁面明顯位置給出原文連接配接,否則保留追究法律責任的權利。
如果文中有什麼錯誤,歡迎指出。以免更多的人被誤導。
收履歷:某網際網路公司,招聘iOS/Android靠譜工程師,入職後,可内部聯系樓主,有小禮品贈送,有意者可郵箱投遞履歷:[email protected]